Ableitung eines Quotienten (Division): Formel und gelöste Aufgaben

In diesem Artikel erklären wir, wie man aus zwei Funktionen einen Quotienten (oder eine Division) ableitet. Sie finden Beispiele für Ableitungen von Funktionsquotienten und können darüber hinaus mit Schritt-für-Schritt-Übungen zu Divisionsableitungen üben.

Formel für die Ableitung eines Quotienten

Die Ableitung eines Koeffizienten (oder einer Division) der Funktionen ist identisch mit der Ableitung der Zählerfunktion durch die Nennerfunktion kleiner als die Zählerfunktion durch die Ableitung der Nennerfunktion dividiert durch das Quadrat der großen Nennerfunktion.

Formel für die Ableitung einer Division oder eines Quotienten

Wie Sie sehen können, haben wir nach der Differentiation immer noch einen Bruch, wenn wir die Regel für die Ableitung eines Quotienten (oder einer Division) anwenden. Aber zusätzlich haben wir im Zähler zwei Multiplikationen und eine Subtraktion, und der Nenner wird mit zwei potenziert.

Beispiele für Ableitungen von Quotienten

Wir haben gerade gesehen, wie die Formel für die Ableitung eines Quotienten zweier Funktionen lautet. Anschließend werden wir einige Beispiele für Ableitungen dieser Art von Operationen lösen. Denken Sie daran: Wenn Sie nicht verstehen, wie ein Funktionsquotient abgeleitet wird, können Sie uns im Kommentarbereich fragen.

Beispiel 1

In diesem Beispiel leiten wir eine Potentialfunktion dividiert durch eine trigonometrische Funktion ab:

$f(x)=\cfrac{3x^2+4x}{\text{sen}(2x)}$

Die Formel für die Ableitung einer Division zweier verschiedener Funktionen lautet wie folgt:

$\begin{array}{c}z(x)=\cfrac{f(x)}{g(x)}\\[2.5ex]\color{orange}\bm{\downarrow}\\[1.5ex] z'(x)=\cfrac{f'(x)\cdot g(x)-f(x)\cdot g'(x)}{\bigl(g(x)\bigr)^2}\end{array}$

Daher müssen wir zunächst die Ableitung jeder Funktion separat berechnen:

$\cfrac{d}{dx}\ (3x^2+4x)=6x+4$

$\cfrac{d}{dx}\ \text{sen}(2x)=2\text{cos}(2x)$

Die Ableitung der gesamten Funktion ist daher:

$\begin{array}{c}f(x)=\cfrac{3x^2+4x}{\text{sen}(2x)}\\[2.5ex]\color{orange}\bm{\downarrow}\\[1.5ex] f'(x)=\cfrac{(6x+4)\cdot\text{sen}(2x)-(3x^2+4x)\cdot 2\text{cos}(2x)}{\text{sen}^2(2x)}\end{array}$

Beispiel 2

In diesem Fall finden wir die Ableitung einer Konstante dividiert durch eine Funktion:

$f(x)=\cfrac{10}{x^2+3x-9}$

Wie wir oben gesehen haben, lautet die Regel für die Ableitung einer Division zweier verschiedener Funktionen wie folgt:

$\begin{array}{c}z(x)=\cfrac{f(x)}{g(x)}\\[2.5ex]\color{orange}\bm{\downarrow}\\[1.5ex] z'(x)=\cfrac{f'(x)\cdot g(x)-f(x)\cdot g'(x)}{\bigl(g(x)\bigr)^2}\end{array}$

Also berechnen wir die Ableitung von Zähler und Nenner getrennt:

$\cfrac{d}{dx}\ 10=0$

$\cfrac{d}{dx}\ (x^2+3x-9)=2x+3$

Und schließlich finden wir die Ableitung der ganzzahligen Division:

$\begin{array}{c}f(x)=\cfrac{10}{x^2+3x-9}\\[2.5ex]\color{orange}\bm{\downarrow}\\[1.5ex] f'(x)=\cfrac{0\cdot (x^2+3x-9)-10\cdot (2x+3)}{\left(x^2+3x-9\right)^2}=\cfrac{-20x+30}{\left(x^2+3x-9\right)^2}\end{array}$

Tatsächlich können wir eine Formel zur direkten Differenzierung ableiten, wenn wir eine Konstante im Zähler dividiert durch eine Funktion haben, da die Ableitung der Konstante immer 0 ist. Daher ist die folgende Formel immer wahr:

$\definecolor{taronjaquadreejemplo}{HTML}{FF9800} \newtcbox{\mymath}[1][]{% nobeforeafter, math upper, tcbox raise base, enhanced, colframe=taronjaquadreejemplo, boxrule=1.1pt, boxsep=2mm, #1} \begin{empheq}[box={\mymath[colback=white, shadow={2mm}{-2mm}{0mm}{taronjaquadreejemplo!20!white,} ]}]{equation*} \begin{array}{c}z(x)=\cfrac{k}{f(x)} \\[2.5ex]\color{orange}\bm{\downarrow}\\[1.5ex] z'(x)=\cfrac{-k\cdot f'(x)}{\bigl(f(x)\bigr)^2}\end{array} \end{empheq}$

Beispiel 3

In dieser Übung werden wir einen Quotienten aus zwei Polynomen ableiten:

$f(x)=\cfrac{x^3+4x^2}{5x^2-8}$

Um die Ableitung zu lösen, müssen wir die Regel für die Ableitung eines Quotienten zweier verschiedener Funktionen anwenden, die wie folgt lautet:

$\begin{array}{c}z(x)=\cfrac{f(x)}{g(x)}\\[2.5ex]\color{orange}\bm{\downarrow}\\[1.5ex] z'(x)=\cfrac{f'(x)\cdot g(x)-f(x)\cdot g'(x)}{\bigl(g(x)\bigr)^2}\end{array}$

Lassen Sie uns nun die Ableitung des Zählerpolynoms und des Nennerpolynoms ermitteln:

$\cfrac{d}{dx}\ (x^3+4x^2)=3x^2+8x$

$\cfrac{d}{dx}\ (5x^2-8)=10x$

Die Ableitung der Division von Polynonymen lautet daher:

$\begin{array}{c}f(x)=\cfrac{x^3+4x^2}{5x^2-8}\\[2.5ex]\color{orange}\bm{\downarrow}\\[1.5ex] f'(x)=\cfrac{(3x^2+8x)\cdot (5x^2-8)-(x^3+4x^2)\cdot 10x}{\left(5x^2-8\right)^2}\end{array}$

Und schließlich führen wir die Operationen durch und vereinfachen den Bruch so weit wie möglich:

$\begin{aligned}f'(x)&=\cfrac{(3x^2+8x)\cdot (5x^2-8)-(x^3+4x^2)\cdot 10x}{\left(5x^2-8\right)^2}\\[2ex]&=\cfrac{15x^4-24x^2+40x^3-64x-10x^4-40x^3}{25x^4+64-80x^2}\\[2ex]&=\cfrac{5x^4-24x^2-64x}{25x^4-80x^2+64}\end{aligned}$

Gelöste Aufgaben zur Ableitung eines Quotienten

Leiten Sie die folgenden Funktionsaufteilungen ab:

$\text{A) }f(x)=\cfrac{9x^2+5x}{6x^3}$

$\text{B) }f(x)=\cfrac{19}{2x^2-2}$

$\text{C) }f(x)=\cfrac{8x^3-4x^2+3x}{e^{4x}}$

$\text{D) }f(x)=\cfrac{\text{cos}(x^2)}{\text{sen}(6x)}$

$\text{E) }f(x)=\cfrac{\ln(x^3+4)}{\left(4x^2-3x\right)^3}$

$\text{F) }f(x)=\cfrac{\sqrt{x^2+4x}}{5^{x^2}}$

Sehen Sie sich die Lösung an

$\begin{aligned}\text{A) }f'(x)&=\cfrac{(18x+5)\cdot 6x^3-(9x^2+5x)\cdot 18x^2}{\left(6x^3\right)^2}\\[1.5ex]&=\cfrac{108x^4+30x^3-162x^4-90x^3}{36x^6}\\[1.5ex]&=\cfrac{-54x^4-60x^3}{36x^6}\\[1.5ex]&=\cfrac{-9x-10}{6x^3}\end{aligned}$

$\text{B) }f'(x)=\cfrac{-19\cdot 4x}{\left(2x^2-2\right)^2}=\cfrac{-76x}{\left(2x^2-2\right)^2}$

$\begin{aligned}\text{C) }f'(x)&=\cfrac{(24x^2-8x+3)e^{4x}-(8x^3-4x^2+3x)\cdot 4e^{4x}}{\left(e^{4x}\right)^2}\\[1.5ex]&=\cfrac{e^{4x}(24x^2-8x+3-32x^3+16x^2-12x)}{e^{8x}}\\[1.5ex]&=\cfrac{-32x^3+40x^2-20x+3}{e^{4x}}\end{aligned}$

$\text{D) }f'(x)=\cfrac{-2x\text{sen}(x^2)\cdot\text{sen}(6x)-\text{cos}(x^2)\text{cos}(6x)\cdot 6}{\text{sen}^2(6x)}$

$\begin{aligned}\text{E) }f'(x)&=\cfrac{\cfrac{3x^2}{x^3+4}\cdot\left(4x^2-3x\right)^3-\ln(x^3+4)\cdot 3\left(4x^2-3x\right)^2\cdot (8x-3) }{\left(\left(4x^2-3x\right)^3\right)^2}\\[1.5ex]&=\cfrac{\cfrac{3x^2}{x^3+4}\cdot\left(4x^2-3x\right)^3-\ln(x^3+4)\cdot 3\left(4x^2-3x\right)^2\cdot (8x-3) }{\left(4x^2-3x\right)^6}\end{aligned}$

$\begin{aligned}\text{F) }f'(x)&=\cfrac{\cfrac{2x+4}{2\sqrt{x^2+4x}}\cdot 5^{x^2} - \sqrt{x^2+4x}\cdot 5^{x^2}\cdot \ln(5) \cdot 2x }{\left(5^{x^2}\right)^2}\\[1.5ex]&=\cfrac{\cfrac{2x+4}{2\sqrt{x^2+4x}}\cdot 5^{x^2} - \sqrt{x^2+4x}\cdot 5^{x^2}\cdot \ln(5) \cdot 2x }{5^{2x^2}}\end{aligned}$

Demonstration der Ableitung eines Quotienten

Abschließend zeigen wir die Formel für die Ableitung einer Division. Dazu verwenden wir die allgemeine Definition einer Ableitung, die lautet:

$\displaystyle f'(x)=\lim_{h \to 0}\frac{f(x+h)-f(x)}{h}$

Sei z eine Division zweier verschiedener Funktionen:

$z(x)=\cfrac{f(x)}{g(x)}$

Dann ist die Ableitung der Funktion z unter Anwendung der mathematischen Definition:

$\displaystyle f'(x)=\lim_{h \to 0}\frac{\cfrac{f(x+h)}{g(x+h)}-\cfrac{f(x)}{g(x)}}{h}$

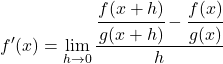
Wir lösen die Subtraktion von Brüchen vom Zähler des Bruchs:

$\displaystyle f'(x)=\lim_{h \to 0}\frac{\cfrac{f(x+h)\cdot g(x)}{g(x+h)\cdot g(x)}-\cfrac{f(x)\cdot g(x+h)}{g(x)\cdot g(x+h)}}{h}$

$\displaystyle f'(x)=\lim_{h \to 0}\frac{f(x+h)\cdot g(x)-f(x)\cdot g(x+h)}{h\cdot g(x)\cdot g(x+h)}$

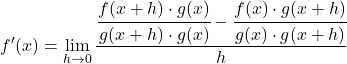
Das Hinzufügen eines Additions- und Subtraktionsterms zu einer Gleichung ändert die Gleichung nicht. Wir können also zum nächsten Schritt übergehen:

$\displaystyle f'(x)=\lim_{h \to 0}\frac{f(x+h)\cdot g(x)\color{orange}\bm{-f(x)\cdot g(x)}\color{black}-f(x)\cdot g(x+h)\color{orange}\bm{+f(x)\cdot g(x)}\color{black}}{h\cdot g(x)\cdot g(x+h)}$

Wir extrahieren den gemeinsamen Faktor:

$\displaystyle f'(x)=\lim_{h \to 0}\frac{g(x)\bigl[f(x+h)-f(x)\bigr]-f(x)\bigl[g(x+h)-g(x)\bigr]}{h\cdot g(x)\cdot g(x+h)}$

Verschieben wir nun den Term h vom Nenner zum Zähler, indem wir die Eigenschaften von Brüchen nutzen:

$\displaystyle f'(x)=\lim_{h \to 0}\frac{g(x)\cdot \cfrac{f(x+h)-f(x)\cdot g(x)}{h}-f(x)\cdot\cfrac{g(x+h)-g(x)}{h}}{g(x)\cdot g(x+h)}$

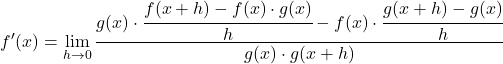
Wir transformieren die Gleichung, indem wir die Eigenschaften der Grenzwerte anwenden:

$\displaystyle f'(x)=\frac{g(x)\cdot \displaystyle\lim_{h \to 0}\cfrac{f(x+h)-f(x)\cdot g(x)}{h}-f(x)\cdot\lim_{h \to 0}\cfrac{g(x+h)-g(x)}{h}}{g(x)\cdot \displaystyle\lim_{h \to 0}g(x+h)}$

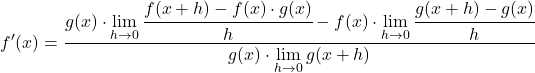
Die Grenzen des Zählers entsprechen genau der mathematischen Definition der Ableitung jeder Funktion, daher:

$\displaystyle f'(x)=\frac{g(x)\cdot f'(x)-f(x)\cdot g'(x)}{g(x)\cdot \displaystyle\lim_{h \to 0}g(x+h)}$

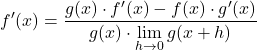
Wir lösen den Grenzwert des Nenners des Bruchs:

$\displaystyle f'(x)=\frac{g(x)\cdot f'(x)-f(x)\cdot g'(x)}{g(x)\cdot g(x)}$

Und so wird die Formel für die Ableitung eines Quotienten zweier Funktionen demonstriert:

$\displaystyle f'(x)=\frac{f'(x)\cdot g(x)-f(x)\cdot g'(x)}{\bigl(g(x)\bigr)^2}$

Ableitung eines quotienten (oder einer division)

Formel für die Ableitung eines Quotienten

Beispiele für Ableitungen von Quotienten

Beispiel 1

Beispiel 2

Beispiel 3

Gelöste Aufgaben zur Ableitung eines Quotienten

Demonstration der Ableitung eines Quotienten

Kommentar verfassen Kommentieren abbrechen