▷ Ableitung einer Subtraktion (Formel und gelöste Aufgaben)

In diesem Artikel erklären wir, wie man eine Subtraktion von Funktionen (Formel) herleitet. Außerdem finden Sie Beispiele für Subtraktionsableitungen und gelöste Schritt-für-Schritt-Übungen zum Üben.

Formel für die Ableitung einer Subtraktion

Die Ableitung der Subtraktion zweier Funktionen ist gleich der separaten Subtraktion der Ableitung jeder Funktion.

$z(x)=f(x)-g(x) \quad\color{orange}\bm{\longrightarrow}\quad\color{black} z'(x)=f'(x)-g'(x)$

Mit anderen Worten: Die separate Differenzierung zweier Funktionen und deren anschließende Subtraktion ist gleichbedeutend damit, zuerst die Funktionen zu subtrahieren und dann die Ableitung zu bilden.

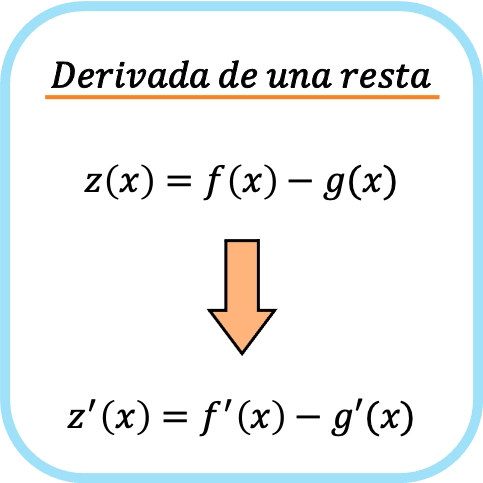
Ebenso gilt die gleiche Differenzierungsregel für Subtraktionen von zwei oder mehr Funktionen. Wenn wir also eine Subtraktion von drei, vier, fünf usw. haben, müssen wir jede einzeln differenzieren und sie dann subtrahieren.

$\begin{array}{c}z(x)=f(x)- g(x)- h(x)- \dots\\[1.5ex]\color{orange}\bm{\downarrow}\quad\color{black} \\[1.5ex]z'(x)=f'(x)-g'(x)- h'(x)- \dots\end{array}$

Wie Sie sehen, ist die Formel für die Ableitung einer Differenz von Funktionen der Regel für die Ableitung einer Summe sehr ähnlich.

➤ Siehe:Ableitung einer Summe von Funktionen

Beispiele für Ableitungen der Subtraktion

Nachdem wir gesehen haben, wie die Formel für die Ableitung einer Subtraktion lautet, analysieren wir nun mehrere Beispiele für Ableitungen dieser Art von Operationen, um vollständig zu verstehen, wie die Subtraktionen von Funktionen abgeleitet werden.

Beispiel 1: Ableitung einer Subtraktion potentieller Funktionen

$f(x)=x^3-4x$

Die Ableitung der Subtraktion zweier Funktionen entspricht der Differenz der Ableitungen jeder einzelnen Funktion. Wir berechnen daher zunächst die Ableitung jeder Funktion einzeln:

$\cfrac{d}{dx} \ x^3=3x^2$

$\cfrac{d}{dx}\ 4x=4$

Die Ableitung der gesamten Funktion ist daher die folgende:

$f'(x)=3x^2-4$

Beispiel 2: Ableitung einer Subtraktion verschiedener Funktionen

$f(x)=\text{cos}(x)-\log_7(x^2)$

Um Subtraktionsfunktionen zu differenzieren, müssen Sie zunächst die beiden Funktionen separat differenzieren und dann subtrahieren.

$\cfrac{d}{dx} \ \text{cos}(x)=-\text{sen}(x)$

$\cfrac{d}{dx}\ \log_7 (x^2)=\cfrac{2x}{x^2\cdot \ln(7)}=\cfrac{2}{x\ln(7)}$

Und nachdem wir die beiden Ableitungen erstellt haben, subtrahieren wir sie in derselben Anfangsreihenfolge:

$f'(x)=-\text{sen}(x)-\cfrac{2}{x\ln(7)}$

Beispiel 3: Ableitung einer quadrierten Subtraktion

$f(x)=\left(x^7-2x^3-9\right)^2$

In diesem Fall haben wir eine zusammengesetzte Funktion, da es sich um eine Subtraktion zwischen drei quadrierten Funktionen handelt. Wir müssen daher die Formel für die Ableitung einer potentiellen Funktion und die Kettenregel verwenden, um die Ableitung der gesamten Funktion zu berechnen:

$f(x)=2\left(x^7-2x^3-9\right)\cdot \left(7x^6-6x^2\right)$

➤ Siehe: Formel für die Ableitung einer Potenz

Gelöste Übungen zur Ableitung einer Subtraktion

Leiten Sie die folgenden Subtraktionen von Funktionen ab:

$\text{A) } f(x)=9x^3-5x$

$\text{B) } f(x)=4x^5-6x^4-x^2-4$

$\text{C) } f(x)=\left(-3x^7-2x^5\right)^4$

$\text{D) } f(x)=\ln(5x^2+3x)-\text{cos}(x)$

$\text{E) } f(x)=8x^3-e^{5x}-\sqrt{8x+2}$

Sehen Sie sich die Lösung an

$\text{A) } f'(x)=27x^2-5$

$\text{B) } f'(x)=20x^4-24x^3-2x$

$\text{C) } f'(x)=4\left(-3x^7-2x^5\right)^3\cdot (-21x^6-10x^4)$

$\text{D) } f'(x)=\cfrac{10x+3}{5x^2+3x}-\bilg(-\text{sen}(x)\bigr)=\cfrac{10x+3}{5x^2+3x}+\text{sen}(x)$

$\text{E) } f'(x)=24x^2-5e^{5x}-\cfrac{8}{2\sqrt{8x+2}}=24x^2-5e^{5x}-\cfrac{4}{\sqrt{8x+2}}$

Beweis der Ableitung einer Subtraktion

Als nächstes demonstrieren wir die Formel für die Ableitung einer Subtraktion von Funktionen aus der Definition der Ableitung, die lautet:

$\displaystyle f'(x)=\lim_{h \to 0}\frac{f(x+h)-f(x)}{h}$

Wenn z also die Differenz zweier verschiedener Funktionen ist:

$z(x)=f(x)-g(x)$

$\displaystyle z'(x)=\lim_{h \to 0}\frac{z(x+h)-z(x)}{h}$

Wir ersetzen z durch die Subtraktion der Funktionen im Grenzwertausdruck:

$\displaystyle z'(x)=\lim_{h \to 0}\frac{\bigl[f(x+h)-g(x+h)\bigr]-\bigl[f(x)-g(x)\bigr]}{h}$

$\displaystyle z'(x)=\lim_{h \to 0}\frac{f(x+h)-g(x+h)-f(x)+g(x)}{h}$

Wir werden nun eine Transformation durchführen, um den Bruch zu trennen und eine Subtraktion zweier Brüche zu erhalten:

$\displaystyle z'(x)=\lim_{h \to 0}\left[\frac{f(x+h)-f(x)}{h}+\frac{-g(x+h)+g(x)}{h}\right]$

$\displaystyle z'(x)=\lim_{h \to 0}\left[\frac{f(x+h)-f(x)}{h}-\frac{g(x+h)-g(x)}{h}\right]$

Durch die Anwendung der Grenzwertgesetze können wir den obigen Ausdruck in zwei verschiedene Grenzwerte aufteilen. Weil der Grenzwert einer Subtraktion gleich der Subtraktion von Grenzwerten ist:

$\displaystyle z'(x)=\lim_{h \to 0}\frac{f(x+h)-f(x)}{h}-\lim_{h \to 0}\frac{g(x+h)-g(x)}{h}$

Wenn man genau hinschaut, entspricht jeder Grenzwert der Ableitung einer Funktion, was bedeutet, dass die Formel für die Ableitung einer Differenz erfüllt ist:

$\displaystyle z'(x)=f'(x)-g'(x)$

Ableitung einer subtraktion