In diesem Artikel erfahren Sie, wie Sie den Kotangens einer Funktion ableiten. Sie finden Beispiele für die Ableitung des Kotangens und sogar Schritt für Schritt gelöste Übungen. Abschließend beweisen wir die Formel für die Ableitung des Kotangens.
Formel für die Ableitung des Kotangens
Die Ableitung des Kotangens von x ist gleich negativ eins über dem Quadrat des Sinus von x. Die Ableitung des Kotangens von x ist ebenfalls gleich minus dem Quadrat des Kosekans von x und minus der Summe von eins plus dem Quadrat des Kotangens von x.
![Rendered by QuickLaTeX.com \begin{array}{c}f(x)=\text{cotg}(x)\\[1.5ex]\color{orange}\bm{\downarrow}\color{black}\\ f'(x)=-\cfrac{1}{\text{sen}^2(x)}=-\text{cosec}^2(x)=-\left(1+\text{cotg}^2(x)\right)\end{array}](https://mathority.org/wp-content/ql-cache/quicklatex.com-0a3653f5c765d773ebc789107bf1a825_l3.png)
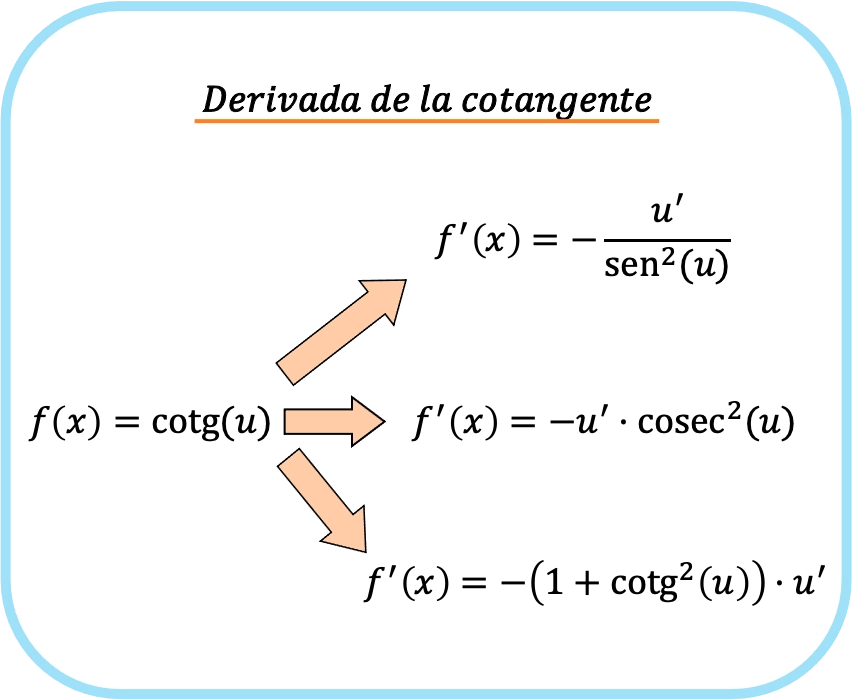
Wenn der Argumentkotangens eine andere Funktion als x ist, sind die Formeln für die Ableitung des Kotangens einer Funktion dieselben wie die vorherigen, jedoch werden die Ausdrücke mit der Ableitung der Funktion des Arguments multipliziert.
![Rendered by QuickLaTeX.com \begin{array}{c}f(x)=\text{cotg}(u)\\[1.5ex]\color{orange}\bm{\downarrow}\color{black}\\ f'(x)=-\cfrac{u'}{\text{sen}^2(u)}=-u' \cdot \text{cosec}^2(u)=-u' \cdot \left(1+\text{cotg}^2(u)\right)\end{array}](https://mathority.org/wp-content/ql-cache/quicklatex.com-38ea1d1edeaf5664c56a946b5a87577d_l3.png)
Das bedeutet, dass es drei verschiedene Formeln gibt, um die Ableitung des Kotangens zu ermitteln. Aber logischerweise ist es nicht notwendig, alle drei Formeln zu verwenden, sondern Sie können es mit der von Ihnen bevorzugten Formel ableiten.
Beispiele für die Ableitung des Kotangens
Nachdem wir nun die Formel für die Ableitung des Kotangens einer Funktion gesehen haben, werden wir in diesem Abschnitt mehrere Beispiele dieser Art trigonometrischer Ableitungen lösen.
Beispiel 1: Ableitung des Kotangens von 2x
In diesem Beispiel werden wir sehen, was die Ableitung des Kotangens der Funktion 2x ist.
![]()
Wie wir gesehen haben, können Sie zur Berechnung der Ableitung des Kotangens eine der drei oben gezeigten Formeln verwenden. In diesem Fall verwenden wir die Sinusformel:
![]()
Da 2x ein Term ersten Grades ist, ist seine Ableitung 2. Die Ableitung des Kotangens von 2x ist also negativ zwei geteilt durch das Quadrat des Sinus von 2x:
![]()
Beispiel 2: Ableitung des Kotangens von x im Quadrat
Im zweiten Beispiel werden wir die Ableitung des Kotangens von x im Quadrat bestimmen.
![]()
In diesem Beispiel ist die Funktion des Kotangens-Arguments kein x, daher müssen wir die Kettenregel anwenden, um den Kotangens zu differenzieren.
![]()
Die Ableitung von x im Quadrat ist 2x, also ist die Ableitung des Kotangens von x 2 :
![]()
Beispiel 3: Ableitung des Kotangens kubiert
Schließlich werden wir herausfinden, wie groß die Ableitung des dritten Kotangens einer Polynomfunktion ist:
![]()
In diesem Fall haben wir eine Zusammensetzung von Funktionen, daher müssen wir die Kettenregel mit der Formel für die Ableitung einer Potenz verwenden, um die Ableitung des Kotangens zu ermitteln:
![]()
Aufgaben zur Ableitung des Kotangens gelöst
Berechnen Sie die Ableitung der folgenden Kotangensfunktionen:
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
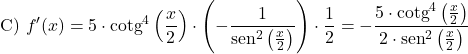
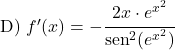
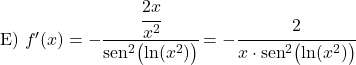
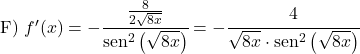
Beweis der Ableitung des Kotangens
In diesem letzten Abschnitt werden wir die Formel für die Ableitung des Kotangens demonstrieren. Dazu beginnen wir mit der mathematischen Definition der Kotangensfunktion, die gleich dem Kosinus dividiert durch den Sinus ist:
![]()
Nun differenzieren wir die Funktion, indem wir die Regel für die Ableitung eines Quotienten anwenden;
![]()
![]()
![]()
Wir nehmen den gemeinsamen Faktor im Nenner und entfernen das negative Vorzeichen aus dem Bruch:
![]()
![]()
Andererseits wissen wir dank der grundlegenden trigonometrischen Identität, dass das Quadrat des Sinus plus das Quadrat des Kosinus gleich eins ist.
![]()
![]()
Und so haben wir die erste Formel für die Ableitung des Kotangens erhalten. Ebenso ist der Kosekans die multiplikative Umkehrung des Sinus, sodass auch die zweite Regel der Ableitung des Kotangens bewiesen ist:
![]()
Schließlich kann die dritte Formel für die Ableitung dieser trigonometrischen Funktion bewiesen werden, indem der Bruch aus dem vorherigen Schritt in eine Summe von Brüchen umgewandelt wird:
![]()
![]()
![]()