Ableitung des Sinus hyperbolicus

Hier erfahren Sie, wie Sie den hyperbolischen Sinus (Formel) herleiten. Darüber hinaus sehen Sie mehrere gelöste Beispiele für die Ableitung des hyperbolischen Sinus. Und schließlich beweisen wir die Formel für die Ableitung dieser Art trigonometrischer Funktion.

Vom hyperbolischen Sinus abgeleitete Formel

Die Ableitung des hyperbolischen Sinus von x ist der hyperbolische Kosinus von x.

$f(x)=\text{senh}(x) \quad\color{orange}\bm{\longrightarrow}\quad\color{black} f'(x)=\text{cosh}(x)$

Daher ist die Ableitung des Sinus hyperbolicus einer Funktion gleich dem Produkt aus dem Kosinus hyperbolicus der Funktion und der Ableitung dieser Funktion.

$f(x)=\text{senh}(u) \quad\color{orange}\bm{\longrightarrow}\quad\color{black} f'(x)=\text{cosh}(u)\cdot u'$

Eigentlich sind die beiden oben genannten Formeln gleich, der einzige Unterschied besteht darin, dass wir in der zweiten Formel die Kettenregel anwenden. Und da die Ableitung von x 1 ist, ändert dies nichts an der Funktion.

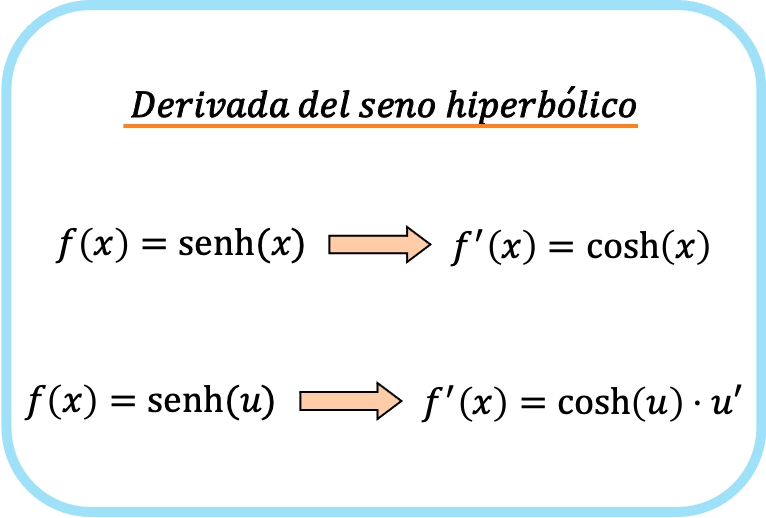
Wie Sie sehen können, ist die Formel für die Ableitung des hyperbolischen Sinus der Formel für die Ableitung des Sinus sehr ähnlich.

Beispiele für die Ableitung des hyperbolischen Sinus

Nachdem wir bereits gesehen haben, wie die Ableitung des hyperbolischen Sinus lautet, gehen wir nun dazu über, mehrere Beispiele für die Ableitung des hyperbolischen Sinus zu lösen. Sie haben also sicherlich keinen Zweifel daran, wie das geht.

Beispiel 1: Ableitung des hyperbolischen Sinus von 2x

$f(x)=\text{senh}(2x)$

In diesem Fall haben wir im Argument des hyperbolischen Sinus eine andere Funktion als x, daher müssen wir die Ableitungsformel des hyperbolischen Sinus mit der Kettenregel verwenden, um die Ableitung zu finden:

$f(x)=\text{senh}(u) \quad\color{orange}\bm{\longrightarrow}\quad\color{black} f'(x)=\text{cosh}(u)\cdot u'$

Die Ableitung von 2x ist 2, daher ist die Ableitung des hyperbolischen Sinus von 2x der hyperbolische Kosinus von 2x mal 2.

$f(x)=\text{senh}(2x) \quad\color{orange}\bm{\longrightarrow}\quad\color{black} f'(x)=\text{cosh}(2x)\cdot 2=2\text{cosh}(2x)$

Beispiel 2: Ableitung des hyperbolischen Sinus von x im Quadrat

$f(x)=\text{senh}(x^2)$

Die Formel für die Ableitung der hyperbolischen Sinusfunktion lautet:

$f(x)=\text{senh}(u) \quad\color{orange}\bm{\longrightarrow}\quad\color{black} f'(x)=\text{cosh}(u)\cdot u'$

Andererseits ist die Ableitung der quadratischen Funktion x ² 2x. Die Ableitung der gesamten Funktion ist daher:

$f(x)=\text{senh}(x^2) \quad\color{orange}\bm{\longrightarrow}\quad\color{black} f'(x)=\text{cosh}(x^2)\cdot 2x$

Beweis der Formel für die Ableitung des hyperbolischen Sinus

Abschließend zeigen wir die Formel für die Ableitung des hyperbolischen Sinus. Dazu gehen wir von der mathematischen Definition des hyperbolischen Sinus aus:

$\text{senh}(x)=\cfrac{e^x-e^{-x}}{2}$