Ableitung des hyperbolischen kosekansbogens

In diesem Artikel erklären wir, wie man den hyperbolischen Arkuskosekans einer Funktion ableitet. Sie finden auch bearbeitete Beispiele für die Ableitung des hyperbolischen Arkuskosekans.

Formel für die Ableitung des hyperbolischen Kosekansbogens

Die Ableitung des bogenhyperbolischen Kosekans von x ist gleich minus 1 dividiert durch das Produkt aus x mal der Wurzel aus eins plus x zum Quadrat.

f(x)=\text{arccsch}(x) \quad\color{orange}\bm{\longrightarrow}\quad\color{black} f'(x)=\cfrac{-1}{x\sqrt{1+x^2}}

Daher ist die Ableitung des Arkushyperbolkosekans einer Funktion minus der Ableitung dieser Funktion dividiert durch das Produkt der Funktion mal der Wurzel aus eins plus der quadrierten Funktion.

f(x)=\text{arccsch}(u) \quad\color{orange}\bm{\longrightarrow}\quad\color{black} f'(x)=\cfrac{-u'}{u\sqrt{1+u^2}}

Zusammenfassend lautet die Formel zur Berechnung der Ableitung der hyperbolischen Arkuskosekansfunktion:

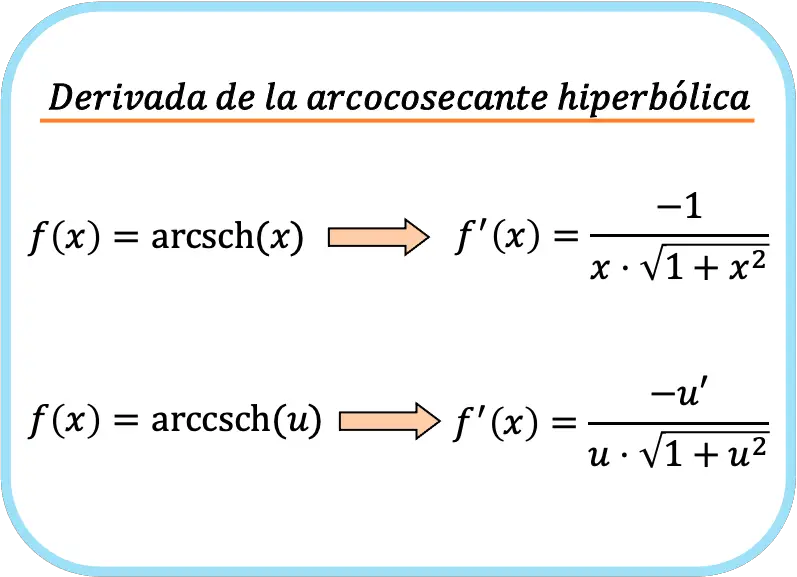
Ableitung des hyperbolischen Kosekansbogens

Obwohl wir zwei Formeln aufgestellt haben, bedeutet das nicht, dass sie unterschiedlich sind. Wenn Sie genau hinschauen, ähnelt die zweite Formel der ersten, wendet jedoch die Kettenregel an.

Beispiele für die Ableitung des hyperbolischen Kosekansbogens

Ausgehend von der Formel für die Ableitung des hyperbolischen Bogenkosekans leiten wir dann zwei solcher Funktionen ab, damit Sie sehen können, wie das geht.

Beispiel 1

f(x)=\text{arccsch}(3x)

In dieser Übung müssen wir die Formel für die Ableitung des Bogenkosekans Hyperbolikus mit der Kettenregel verwenden, da es im Argument eine von x verschiedene Funktion gibt:

f(x)=\text{arccsch}(u) \quad\color{orange}\bm{\longrightarrow}\quad\color{black} f'(x)=\cfrac{-u'}{u\sqrt{1+u^2}}

Um die Ableitung zu finden, müssen wir also u durch 3x und u‘ durch seine Ableitung, also 3, ersetzen:

f(x)=\text{arccsch}(3x) \quad\color{orange}\bm{\longrightarrow}\quad\color{black} f'(x)=\cfrac{-3}{3x\sqrt{1+(3x)^2}}=\cfrac{-3}{3x\sqrt{1+9x^2}}

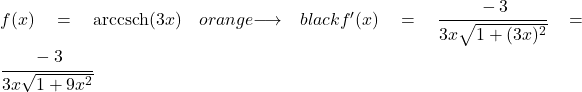
Beispiel 2

f(x)=\text{arccsch}(x^5-2x^3)

In diesem Fall haben wir eine Polynomfunktion im hyperbolischen Arkuskosekans-Argument, daher müssen wir auch die Kettenregel verwenden, um sie abzuleiten:

f(x)=\text{arccsch}(u) \quad\color{orange}\bm{\longrightarrow}\quad\color{black} f'(x)=\cfrac{-u'}{u\sqrt{1+u^2}}

Also setzen wir die Ableitung der Argumentfunktion in den Zähler des Bruchs und ändern im Nenner das u durch die Polynomfunktion:

\begin{aligned}f(x)=\text{arccsch}(x^5-2x^3) \quad\color{orange}\bm{\longrightarrow}\quad\color{black}f'(x)&=\cfrac{-(5x^4-6x^2)}{(x^5-2x^3)\sqrt{1+(x^5-2x^3)^2}}\\[1.5ex] &=\cfrac{-5x^4+6x^2}{(x^5-2x^3)\sqrt{1+(x^5-2x^3)^2}}\end{aligned}

ähnliche Gegenstände

Kommentar verfassen

Deine E-Mail-Adresse wird nicht veröffentlicht. Erforderliche Felder sind mit * markiert

Nach oben scrollen