Hier erklären wir, wie man den hyperbolischen Kotangens einer Funktion ableitet. Außerdem finden Sie Beispiele für die Ableitung des hyperbolischen Kotangens.
Formel für die Ableitung des hyperbolischen Kotangens
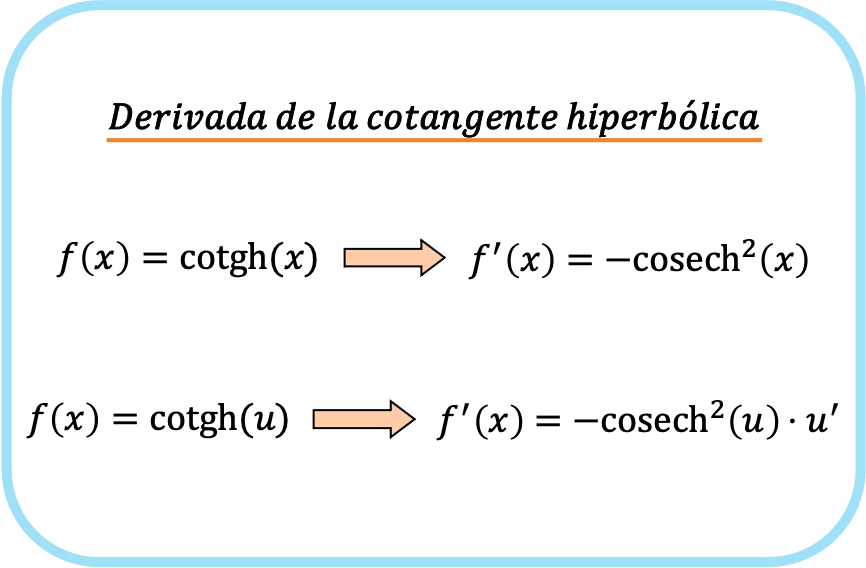
Die Ableitung des hyperbolischen Kotangens von x ist gleich minus dem hyperbolischen Kosekans von x im Quadrat.
![]()
Daher ist die Ableitung des hyperbolischen Kotangens einer Funktion minus dem hyperbolischen Kosekans der Funktion mal der Ableitung dieser Funktion.
![]()
Beachten Sie, dass in der zweiten Formel die Kettenregel angewendet wurde und diese Formel verwendet wird, wenn das Argument des hyperbolischen Kotangens eine andere Funktion als x enthält.
In einigen Mathematikbüchern finden Sie möglicherweise, dass die Ableitung des Kotangens eine andere ist, da die folgenden drei Ausdrücke äquivalent sind:
![]()
Natürlich können Sie jeden der drei Ausdrücke verwenden, den Sie bevorzugen, um den hyperbolischen Kotangens abzuleiten, am häufigsten wird jedoch der hyperbolische Kosekans im Quadrat verwendet.
Beispiele für die Ableitung des hyperbolischen Kotangens
Sobald wir die Formel für die Ableitung des hyperbolischen Kotangens einer Funktion kennen, werden wir mehrere Beispiele dieser Art trigonometrischer Ableitungen lösen.
Beispiel 1
In diesem Beispiel werden wir sehen, was die Ableitung des hyperbolischen Kotangens der Funktion 2x ist.
![]()
Im hyperbolischen Kotangens-Argument haben wir eine andere Funktion als x, daher müssen wir die Formel mit der Kettenregel verwenden, um die Ableitung durchzuführen:
![]()
Da 2x ein Term ersten Grades ist, ist seine Ableitung 2. Um also die Ableitung des hyperbolischen Kotangens von 2x zu finden, setzen wir einfach 2x in das quadrierte Argument des hyperbolischen Kosekans ein und multiplizieren mit 2.
![]()
Beispiel 2
Im zweiten Beispiel bestimmen wir den Wert der Ableitung des hyperbolischen Kotangens einer Polynomfunktion.
![]()
Wie wir oben gesehen haben, lautet die Regel zur Ableitung des hyperbolischen Kotangens einer Funktion wie folgt:
![]()
Daher lautet die Ableitung des hyperbolischen Kotangens dieser Übung wie folgt:
![]()