In diesem Artikel erklären wir, wie man den hyperbolischen Kosekans einer Funktion ableitet. Darüber hinaus können Sie mehrere gelöste Beispiele für die Ableitung des hyperbolischen Kosekans sehen.
Formel für die Ableitung des hyperbolischen Kosekans
Die Ableitung des hyperbolischen Kosekans von x ist gleich minus dem hyperbolischen Kosekans von x mal dem hyperbolischen Kotangens von x.
![]()
Daher ist die Ableitung des hyperbolischen Kosekans einer Funktion minus dem Produkt aus dem hyperbolischen Kosekans der Funktion mal dem hyperbolischen Kotangens der Funktion mal der Ableitung dieser Funktion.
![]()
Kurz gesagt lautet die Formel zur Ableitung des Kosekans einer Funktion:
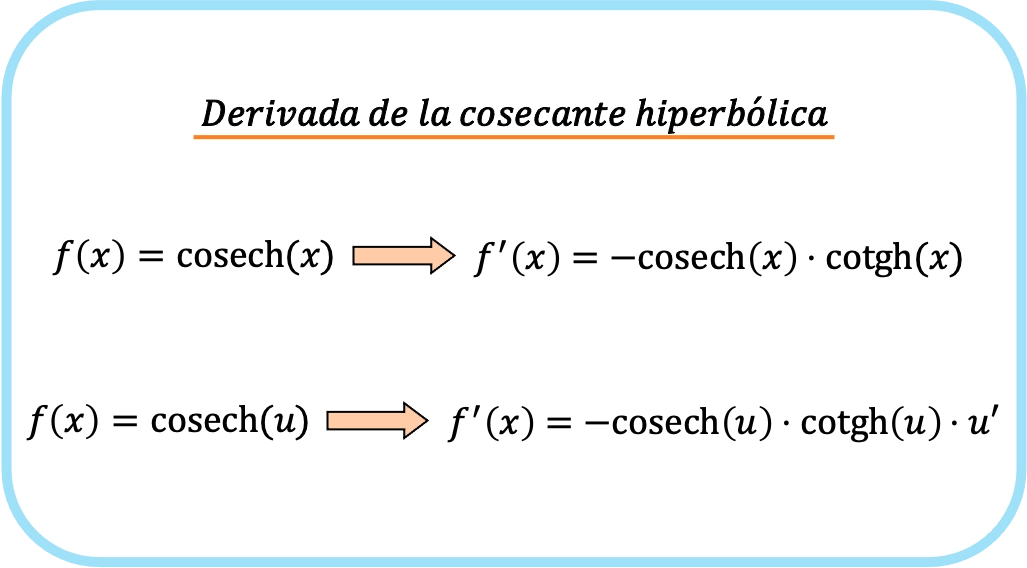
Tatsächlich entsprechen die beiden vorherigen Ausdrücke einer einzigen Formel. Der Unterschied besteht darin, dass die Kettenregel in der zweiten Formel angewendet wird.
Beispiele für die Ableitung des hyperbolischen Kosekans
Nachdem wir gesehen haben, wie die Formel für die Ableitung des hyperbolischen Kosekans lautet, finden Sie hier einige Beispiele für diese Art trigonometrischer Ableitung.
Beispiel 1
In diesem ersten Beispiel werden wir den hyperbolischen Kosekans von x im Quadrat ableiten:
![]()
Die Funktion des Arguments des hyperbolischen Kosekans unterscheidet sich von x, daher müssen wir die Formel für die Ableitung des hyperbolischen Kosekans mit der Kettenregel verwenden.
![]()
Um diese trigonometrische Funktion abzuleiten, müssen wir also lediglich die Werte in der vorherigen Formel ersetzen, d. h. im Argument des hyperbolischen Kosekans und des hyperbolischen Tangens setzen wir x 2 ein und multiplizieren alles mit der Ableitung von x zum Quadrat, also 2x:
![]()
Beispiel 2
In dieser Übung werden wir sehen, wie groß die Ableitung des hyperbolischen Kosekans von x in die Kubikzahl ist:
![]()
Um die Ableitung des hyperbolischen Kosekans einer Funktion zu finden, wenden wir deren Formel an:
![]()
Die Ableitung von x quadriert ist 3x 2 , also ist die Ableitung der gesamten Funktion:
![]()