In diesem Artikel erklären wir, wie man den hyperbolischen Arkuskotangens einer Funktion ableitet. Darüber hinaus können Sie gelöste Beispiele für die Ableitung des hyperbolischen Arkuskotangens sehen.
Formel für die Ableitung des hyperbolischen Arkuskotangens
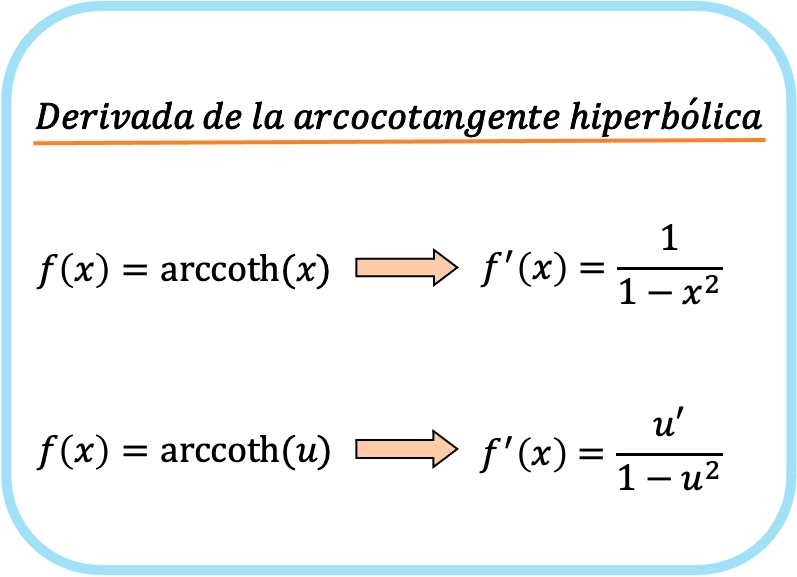
Die Ableitung des hyperbolischen Arkuskotangens von x ist eins über eins minus x zum Quadrat.
![]()
Daher ist die Ableitung des hyperbolischen Arkuskotangens einer Funktion gleich dem Quotienten der Ableitung dieser Funktion geteilt durch eins minus dem Quadrat dieser Funktion.
![]()
Beachten Sie, dass die zweite Formel der ersten ähnelt, jedoch die Kettenregel anwendet, sodass sie tatsächlich als dieselbe Formel betrachtet werden können.
In einigen Mathematikbüchern sehen Sie möglicherweise, dass die Ableitung dieser Art von inverser trigonometrischer Funktion wie folgt lautet:
![]()
Wenn Sie jedoch genau hinsehen, handelt es sich um dieselbe Formel. Der einzige Unterschied besteht darin, dass Zähler und Nenner des Bruchs mit -1 multipliziert wurden.
Beispiele für die Ableitung des hyperbolischen Arkuskotangens
Beispiel 1
![]()
Im hyperbolischen Arkuskotangens-Argument haben wir eine Funktion, die sich von x unterscheidet, daher müssen wir die Kettenregelformel verwenden, um sie abzuleiten:
![]()
Die Ableitung von 5x ist 5, also setzen Sie eine 5 in den Zähler des Bruchs und ein Minus 5x zum Quadrat in den Nenner:
![]()
Beispiel 2
![]()
Um die Ableitung dieser Funktion zu ermitteln, müssen wir die Formel für die Ableitung des hyperbolischen Arkuskotangens anwenden, die wie folgt lautet:
![]()
In diesem Fall haben wir eine zusammengesetzte Funktion, da das Argument der trigonometrischen Funktion eine Exponentialfunktion enthält. Wir müssen also die Kettenregel verwenden, um die Ableitung der gesamten Funktion zu finden:
![]()