Hier erfahren Sie, wie Sie die Ableitung des hyperbolischen Arcsecans einer Funktion berechnen. Darüber hinaus können Sie gelöste Beispiele für die Ableitung des hyperbolischen Bogensekans sehen.
Hyperbolische Arcsecant-Ableitungsformel
Die Ableitung des hyperbolischen Arcsecant von x ist gleich minus 1 dividiert durch das Produkt aus x mal der Wurzel aus eins minus x zum Quadrat.
![]()
Daher ist die Ableitung des hyperbolischen Arcsecants einer Funktion minus der Ableitung dieser Funktion dividiert durch das Produkt der Funktion mal der Wurzel aus eins minus der quadrierten Funktion.
![]()
Kurz gesagt lautet die Formel für die Ableitung der hyperbolischen Arcsecant-Funktion:
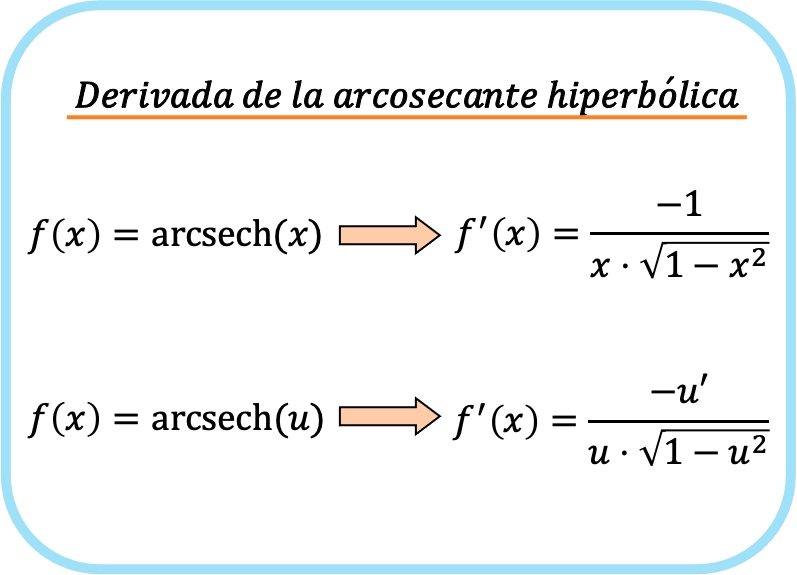
Eigentlich entsprechen beide Ausdrücke der gleichen Formel, allerdings wird auf die zweite Formel die Kettenregel angewendet. Wenn Sie u durch die Identitätsfunktion x ersetzen, erhalten Sie tatsächlich die erste Formel, da die Ableitung von x 1 ist.
Beispiele für die Ableitung des hyperbolischen Arcsecans
Nachdem wir gesehen haben, wie die Formel für die Ableitung des hyperbolischen Arcsecans lautet, werden wir zwei Schritt-für-Schritt-Übungen dieser Art von inversen trigonometrischen Ableitungen lösen. So können Sie genau sehen, wie Sie den hyperbolischen Arcsecans einer Funktion ableiten.
Beispiel 1
In diesem Beispiel bestimmen wir die Ableitung des 2x hyperbolischen Arcsecans.
![]()
Im hyperbolischen Arcsecant-Argument haben wir eine andere Funktion als x, daher müssen wir die Kettenregelformel verwenden, um sie abzuleiten:
![]()
Die Funktion 2x ist linear, daher ist ihre Ableitung 2. Um die Ableitung zu finden, ersetzen wir einfach 2x für u und 2 für u‘ in der Formel:
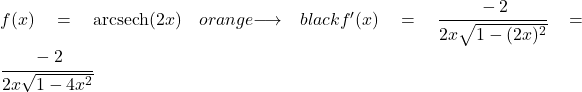
Beispiel 2
In dieser zweiten Übung werden wir den hyperbolischen Arcsecans einer Polynomfunktion ableiten:
![]()
Die Funktion dieser Übung ist zusammengesetzt, da der hyperbolische Arcsecans in seiner Argumentation eine andere Funktion hat. Daher müssen wir zur Ableitung die hyperbolische Arcsecant-Ableitungsformel mit der Kettenregel verwenden:
![]()
Deshalb setzen wir im Zähler des Bruchs die Ableitung der Polynomfunktion des Arguments ein und im Nenner ändern wir das u durch die Polynomfunktion:
![Rendered by QuickLaTeX.com \begin{aligned}f(x)=\text{arcsech}(x^3-4x) \quad\color{orange}\bm{\longrightarrow}\quad\color{black}f'(x)&=\cfrac{-(3x^2-4)}{(x^3-4x)\sqrt{1-(x^3-4x)^2}}\\[1.5ex] &=\cfrac{-3x^2+4}{(x^3-4x)\sqrt{1-(x^3-4x)^2}}\end{aligned}](https://mathority.org/wp-content/ql-cache/quicklatex.com-1f6389de5c7761fb5d35a9861156eec1_l3.png)