Hier erfahren Sie, wie Sie den Sekanten einer Funktion ableiten. Darüber hinaus können Sie mehrere Schritt für Schritt gelöste Übungen zur Ableitung der Sekante sehen. Und schließlich finden Sie die Demonstration der Formel für diese Art trigonometrischer Ableitung.
Was ist die Ableitung der Sekante?
Die Ableitung der Sekante von x ist gleich dem Produkt aus der Sekante von x und dem Tangens von x.
![]()
Durch Anwendung trigonometrischer Formeln kann die Ableitung der Sekante von x auch als Quotient aus dem Sinus von x geteilt durch das Quadrat des Kosinus von x definiert werden.
![]()
Und wenn wir die Kettenregel anwenden, ist die Ableitung der Sekante einer Funktion das Produkt aus der Sekante der Funktion mal dem Tangens der Funktion mal der Ableitung der Funktion.
![]()
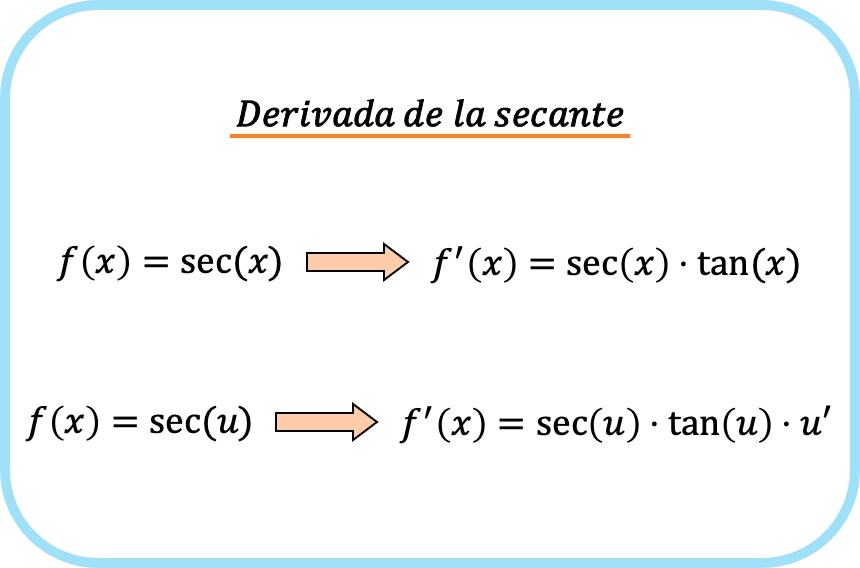
Zusammenfassend lautet die Formel für die Ableitung der Sekantenfunktion wie folgt:
Beispiele für die Ableitung der Sekante
Sobald wir gesehen haben, wie die Formel für die Ableitung der Sekante lautet, werden wir mehrere Beispiele dieser Art trigonometrischer Ableitungen lösen.
Beispiel 1: Ableitung der Sekante von 2x
In diesem Beispiel sehen wir, wie viel die Ableitung der Sekante von 2x wert ist:
![]()
Um den Sekanten der 2x-Funktion abzuleiten, müssen Sie die entsprechende Formel verwenden. Außerdem haben wir im Sekantenargument eine andere Funktion als x, daher müssen wir die Kettenregel anwenden.
![]()
Die Funktion 2x ist linear, daher ist ihre Ableitung 2. Um die Ableitung zu finden, ersetzen wir daher einfach das u durch 2x und das u‘ durch 2 in der Formel:
![]()
Beispiel 2: Ableitung des Sekanten von x im Quadrat
In dieser Übung werden wir sehen, was die Ableitung der Sekante von x im Quadrat ist:
![]()
Um die Sekante einer Funktion abzuleiten, können Sie eine der beiden oben gezeigten Formeln verwenden. In diesem Fall unterscheiden wir die Funktion jedoch mit der Formel für die Multiplikation zwischen Sekante und Tangente.
![]()
Die Ableitung von x hoch mit 2 ergibt 2x, daher ist die Ableitung der Sekante von x im Quadrat:
![]()
Beispiel 3: Ableitung der Sekantenkube eines Polynoms
![]()
Die Regel für die Ableitung der Sekante einer Funktion lautet:
![]()
Aber in diesem Fall müssen wir eine zusammengesetzte Funktion ableiten, da die Sekante in die dritte Potenz erhoben wird und wir darüber hinaus in ihrem Argument eine Polynomfunktion haben. Um also die gesamte Funktion zu differenzieren, müssen wir die Kettenregel anwenden:
![Rendered by QuickLaTeX.com \begin{aligned}f'(x)& =3\text{sec}^2(x^5+4x^2-3)\text{sec}(x^5+4x^2-3)\text{tan}(x^5+4x^2-3)(5x^4+8x)\\[1.5ex]&=3\text{sec}^3(x^5+4x^2-3)\text{tan}(x^5+4x^2-3)(5x^4+8x)\end{aligned}](https://mathority.org/wp-content/ql-cache/quicklatex.com-7ab88cc23ab3fb559e2386cd52637082_l3.png)
Gelöste Übungen zur Ableitung einer Sekante
Leiten Sie die folgenden Sekantenfunktionen ab:
![]()
![]()
![]()
![]()
![]()
![]()
![Rendered by QuickLaTeX.com \begin{aligned}\text{B) }f(x)& =4\text{sec}^3(5x^4)\cdot \text{sec}(5x^4)\cdot \text{tan}(5x^4)\cdot 20x^3\\[1.5ex] &=4\text{sec}^4(5x^4)\cdot \text{tan}(5x^4)\cdot 20x^3\end{aligned}](https://mathority.org/wp-content/ql-cache/quicklatex.com-72985d8bce95d808b9070bc7b834b271_l3.png)
![]()
![]()
![]()
Demonstration der Formel für die Ableitung der Sekante
Als nächstes beweisen wir die Formel für die Ableitung der Sekante. Obwohl es natürlich nicht notwendig ist, den Beweis auswendig zu kennen, ist es immer gut zu verstehen, woher die Formeln stammen.
Mathematisch gesehen ist die Definition der Sekante die multiplikative Umkehrung des Kosinus:
![]()
Daher können wir versuchen, die Sekante mithilfe der Quotientenregel abzuleiten:
![]()
Und wie wir im ersten Abschnitt gesehen haben, kann der vorherige Ausdruck in die Formel für die Ableitung der Sekante umgewandelt werden. Dazu teilen wir den Bruch in zwei verschiedene Brüche auf:
![]()
Die Division des Sinus durch den Cosinus entspricht dem Tangens, wir ersetzen daher den genannten Quotienten durch den Tangens:
![]()
Nach der mathematischen Definition der Sekantenfunktion ist der Kosinus ihr inverser Multiplikativ. Indem wir also eins dividiert durch den Kosinus durch die Sekante ersetzen, erhalten wir die Formel für seine Ableitung:
![]()