In diesem Artikel erklären wir, wie man den hyperbolischen Sekanten einer Funktion ableitet. Sie finden die Formel für die Ableitung des hyperbolischen Sekants und mehrere Beispiele für diese Art von Ableitung.
Formel für die Ableitung der hyperbolischen Sekante
Die Ableitung des hyperbolischen Sekantes von x ist gleich minus dem Produkt aus dem hyperbolischen Sekante von x mal dem hyperbolischen Tangens von x.
![]()
Daher ist die Ableitung des hyperbolischen Sekanten einer Funktion minus dem Produkt aus dem hyperbolischen Sekanten der Funktion mal dem hyperbolischen Tangens der Funktion mal der Ableitung dieser Funktion.
![]()
Kurz gesagt lautet die Formel für die Ableitung der hyperbolischen Sekantenfunktion:
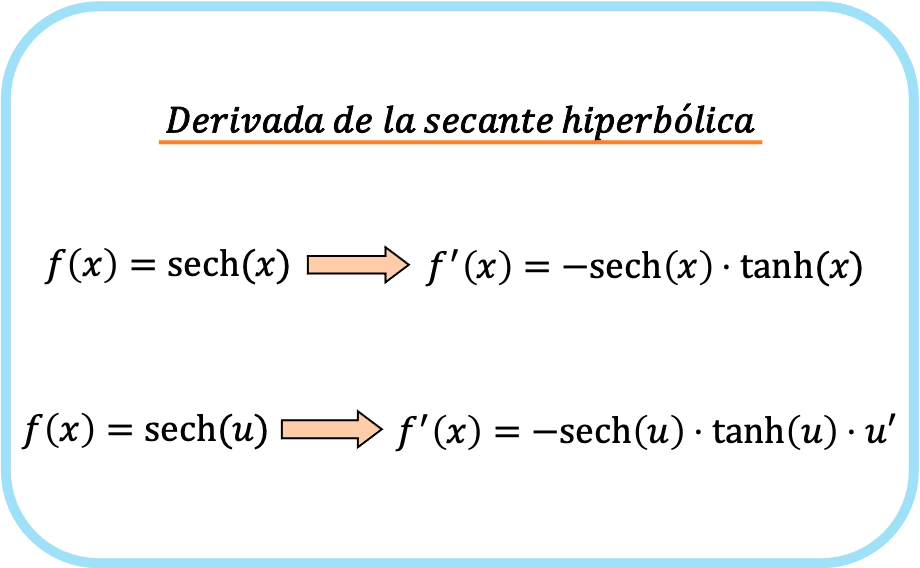
Beachten Sie, dass beide Ausdrücke tatsächlich zu einer einzigen Formel gehören. Der einzige Unterschied besteht darin, dass in der zweiten Formel die Kettenregel angewendet wird.
Beispiele für die Ableitung der hyperbolischen Sekante
Nachdem wir nun die Formel für die Ableitung der hyperbolischen Sekante kennen, werden wir mehrere gelöste Übungen dieser Art der trigonometrischen Ableitung sehen.
Beispiel 1
![]()
In diesem Beispiel haben wir im hyperbolischen Sekantenargument eine andere Funktion als x, daher müssen wir zur Ableitung die Kettenregelformel verwenden.
![]()
Da die Funktion 2x linear ist, ist ihre Ableitung 2. Um die Ableitung zu finden, ersetzen wir daher einfach das u durch 2x und das u‘ durch 2 in der Formel:
![]()
Beispiel 2
![]()
Die Funktion dieser Übung ist zusammengesetzt, da die hyperbolische Sekante in ihrem Argument eine andere Funktion hat. Wir müssen daher die hyperbolische Sekantenformel mit der Kettenregel verwenden, um sie abzuleiten:
![]()
Die auf 2 erhöhte Ableitung von x ergibt 2x, daher ist die Ableitung des hyperbolischen Sekanten von x im Quadrat:
![]()