Kettenregel (ableitungen)

Hier erfahren Sie, was eine Kettenregel ist und wie Sie mithilfe der Kettenregel Funktionen ableiten. Darüber hinaus können Sie mehrere Beispiele für Ableitungen sehen, die mit der Kettenregel gelöst wurden, und Sie können sogar Schritt für Schritt gelöste Übungen zu Ableitungen unter Anwendung der Kettenregel üben.

Was ist die Kettenregel?

Die Kettenregel ist eine Formel zur Ableitung zusammengesetzter Funktionen. Die Kettenregel besagt, dass die Ableitung einer zusammengesetzten Funktion f(g(x)) gleich der Ableitung f'(g(x)) multipliziert mit der Ableitung g'(x) ist.

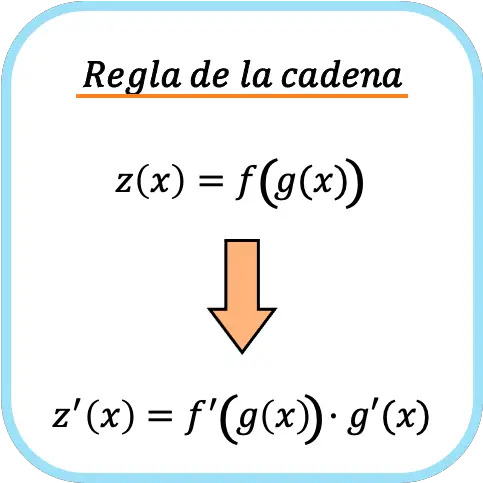
Kettenregel

➤ Siehe: zusammengesetzte Funktion

Informell wird oft gesagt, dass die Kettenregel darin besteht , die Funktion zu differenzieren und sie dann mit dem zu multiplizieren, was darin enthalten ist .

Mit der Kettenregelformel können wir zusammengesetzte Funktionen viel einfacher differenzieren, denn wenn wir eine Zusammensetzung von Funktionen anhand des Grenzwerts der Ableitungsdefinition differenzieren würden, müssten wir viele Berechnungen durchführen.

Andererseits muss berücksichtigt werden, dass diese Regel nur zur Ermittlung der Ableitung zusammengesetzter Funktionen und nicht von Funktionen jeglicher Art oder Operationen mit Funktionen verwendet wird. Ein sehr häufiger Fehler besteht beispielsweise darin, etwas falsch zu machen und die Kettenregel auf funktionale Produkte wie die folgenden anzuwenden:

\ln(x)\cdot x^2

❌

Die Kettenregel kann nur verwendet werden , wenn eine Funktion in einer anderen enthalten ist .

\ln(x^2)

✅

Beispiele für Ableitungen mit der Kettenregel

Angesichts der Definition der Kettenregel werden wir am Beispiel der Kettenregel mehrere Funktionen ableiten. Denken Sie daran: Wenn Sie in einem Beispiel nicht verstehen, wie die Funktion mit der Kettenregel abgeleitet wird, können Sie uns in den Kommentaren fragen!

Beispiel 1

In diesem Beispiel verwenden wir die Kettenregel, um den natürlichen Logarithmus von x zum Quadrat abzuleiten:

f(x)=\ln(x^2)

Die Ableitung des natürlichen Logarithmus ist gleich dem 1-fachen seines Arguments, also der Ableitung

f'\bigl(g(x)\bigr)

Sei:

f(x)=\ln(u) \quad\color{orange}\bm{\longrightarrow}\quad\color{black} f'(x)=\cfrac{1}{u}

f\bigl(g(x)\bigr)=\ln(x^2) \quad\color{orange}\bm{\longrightarrow}\quad\color{black} f'\bigl(g(x)\bigr)=\cfrac{1}{x^2}

Andererseits ist die Ableitung von x hoch zwei 2x:

g(x)=x^2\quad\color{orange}\bm{\longrightarrow}\quad\color{black} g'(x)=2x

Abschließend berechnen wir die Ableitung der gesamten Funktion, indem wir die Kettenregel anwenden. Die Ableitung der zusammengesetzten Funktion ist das Produkt der beiden Ableitungen, die wir gerade gefunden haben:

z(x)=f\bigl(g(x)\bigr) \quad\color{orange}\bm{\longrightarrow}\quad\color{black}z'(x)=f'\bigl(g(x)\bigr)\cdot g'(x)

f(x)=\ln(x^2) \quad\color{orange}\bm{\longrightarrow}\quad\color{black} f'(x)=\cfrac{1}{x^2}\cdot 2x = \cfrac{2x}{x^2}=\cfrac{2}{x}

Beispiel 2

In diesem zweiten Beispiel leiten wir eine Potentialfunktion basierend auf einem Polynom ab:

f(x)=\left(3x^2+4x-5\right)^3

Um eine Potenz abzuleiten, müssen wir den ursprünglichen Exponenten davor platzieren und eine Einheit vom Exponenten subtrahieren. Die Ableitung der Potentialfunktion ohne Anwendung der Kettenregel wäre also:

f\bigl(g(x)\bigr)=\left(3x^2+4x-5\right)^3 \quad\color{orange}\bm{\longrightarrow}\quad\color{black} f'\bigl(g(x)\bigr)=3\left(3x^2+4x-5\right)^2

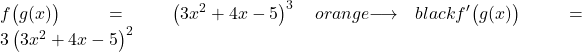
Jetzt leiten wir ab, was in Klammern steht:

g(x)=3x^2+4x-5\quad\color{orange}\bm{\longrightarrow}\quad\color{black} g'(x)=6x+4

Und schließlich verwenden wir die Kettenregel, um die Ableitung der gesamten Funktion zu lösen, die die Multiplikation der beiden zuvor berechneten Ableitungen sein wird:

z(x)=f\bigl(g(x)\bigr) \quad\color{orange}\bm{\longrightarrow}\quad\color{black}z'(x)=f'\bigl(g(x)\bigr)\cdot g'(x)

f(x)=\left(3x^2+4x-5\right)^3 \quad\color{orange}\bm{\longrightarrow}\quad\color{black} f'(x)=3\left(3x^2+4x-5\right)^2\cdot (6x+4)

Beispiel 3

In diesem Fall werden wir nach der Sinusableitung von x kubisch plus 7x auflösen:

f(x)=\text{sen}(x^3+7x)

Tatsächlich handelt es sich um eine Zusammensetzung von Funktionen, da wir die Funktion x 3 +7x innerhalb der Sinusfunktion haben. Daher können wir die Kettenregel verwenden, um die Ableitung der zusammengesetzten Funktion zu finden.

Einerseits ist die Ableitung des Sinus der Kosinus, daher ist die Ableitung der äußeren Funktion der Kosinus mit demselben Argument wie der Sinus:

f\bigl(g(x)\bigr)=\text{sen}(x^3+7x) \quad\color{orange}\bm{\longrightarrow}\quad\color{black} f'\bigl(g(x)\bigr)=\text{cos}(x^3+7x)

Und andererseits ist die Ableitung von x 3 +7x 3x 2 +7.

g(x)=x^3+7x\quad\color{orange}\bm{\longrightarrow}\quad\color{black} g'(x)=3x^2+7

Daher ist die Ableitung der zusammengesetzten Funktion das Produkt der beiden Ableitungen:

z(x)=f\bigl(g(x)\bigr) \quad\color{orange}\bm{\longrightarrow}\quad\color{black}z'(x)=f'\bigl(g(x)\bigr)\cdot g'(x)

f(x)=\text{sen}(x^3+7x) \quad\color{orange}\bm{\longrightarrow}\quad\color{black} f'(x)=\text{cos}(x^3+7x)\cdot (3x^2+7)

Aufgaben zu Ableitungen mit der Kettenregel gelöst

Übung 1

Leiten Sie die folgende zusammengesetzte Funktion mithilfe der Kettenregel ab:

f(x)=\left(5x^2-6x\right)^3

Die äußere Funktion ist eine potentielle Funktion, daher müssen Sie zur Berechnung ihrer Ableitung die folgende Formel anwenden:

f\bigl(g(x)\bigr)=a\bigl(g(x)\bigr)^n \ \longrightarrow \ f'\bigl(g(x)\bigr)=n\cdot a\bigl(g(x)\bigr)^{n-1}

f\bigl(g(x)\bigr)=\left(5x^2-6x\right)^3\ \longrightarrow \ f'\bigl(g(x)\bigr)= 3\left(5x^2-6x\right)^2

Und dann berechnen wir die Ableitung der darin enthaltenen Funktion. Da es sich um eine Subtraktion von Potenzen handelt, müssen Sie zur Berechnung ihrer Ableitung die folgende Formel auf jeden ihrer Terme anwenden:

f(x)=ax^n \ \longrightarrow \ f'(x)=n\cdot ax^{n-1}

g(x)=5x^2-6x\ \longrightarrow

g'(x)=2\cdot 5x^1-1 \cdot 6 x^0 =10x-6

Kurz gesagt, die Ableitung der zusammengesetzten Funktion ist das Produkt der beiden gefundenen Ableitungen:

z(x)=f\bigl(g(x)\bigr) \ \longrightarrow \ z'(x)=f'\bigl(g(x)\bigr)\cdot g'(x)

f(x)=\left(5x^2-6x\right)^3 \ \longrightarrow \ \bm{f'(x)= 3\left(5x^2-6x\right)^2\cdot (10x-6)}

Übung 2

Lösen Sie die Ableitung der folgenden zusammengesetzten Funktion mithilfe der Kettenregel:

f(x)=-3\left(5x^5+9x^3\right)^4

Zuerst ermitteln wir die Ableitung der äußeren Funktion:

\begin{aligned} f\bigl(g(x)\bigr) \ \longrightarrow \ f'\bigl(g(x)\bigr) & =4 \cdot ( -3) \left(5x^5+9x^3\right)^3 \\[1.5ex]&=-12\left(5x^5+9x^3\right)^3 \end{aligned}

Und jetzt lösen wir die Ableitung der inneren Funktion:

g(x)=5x^5+9x^3\ \longrightarrow \ g'(x)=25x^4+27x^2

Die Ableitung der gesamten Funktion ist daher:

z(x)=f\bigl(g(x)\bigr) \ \longrightarrow \ z'(x)=f'\bigl(g(x)\bigr)\cdot g'(x)

f(x)=-3\left(5x^5+9x^3\right)^4 \ \longrightarrow \ \bm{f'(x)=-12\left(5x^5+9x^3\right)^3\cdot \left(25x^4+27x^2\right)}

Übung 3

Berechnen Sie die Ableitung der folgenden Funktionszusammensetzung mit der Kettenregel:

f(x)=e^{2x^3}

Da es sich um eine Exponentialfunktion handelt, müssen Sie zur Berechnung ihrer Ableitung die folgende Formel anwenden:

f(x)=e^{x} \ \longrightarrow \ f'(x)=e^{x}

f\bigl(g(x)\bigr)=e^{2x^3} \ \longrightarrow \ f'\bigl(g(x)\bigr)= e^{2x^3}

Wir unterscheiden die Funktion auch vom Exponenten der Funktion:

g(x)=2x^3 \ \longrightarrow \ g'(x)=6x^2

Und wir verwenden die Kettenregel, um die Ableitung der ganzzahligen zusammengesetzten Funktion zu finden:

z(x)=f\bigl(g(x)\bigr) \ \longrightarrow \ z'(x)=f'\bigl(g(x)\bigr)\cdot g'(x)

f(x)=e^{2x^3} \ \longrightarrow \ \bm{f'(x)= e^{2x^3}\cdot 6x^2}

Übung 4

Finden Sie die Ableitung der folgenden zusammengesetzten Funktion mithilfe der Kettenregel:

f(x)=\sqrt[3]{\text{sen}(x) +x }

Dies ist eine Zusammensetzung von Funktionen, da wir im Argument einer irrationalen Funktion eine Sinusfunktion und eine lineare Funktion haben. Also berechnen wir zunächst die Ableitung der Wurzel:

f(x)=\sqrt[n]{x} \ \longrightarrow \ f'(x)=\cfrac{1}{n\sqrt[n]{x^{n-1}}}

f\bigl(g(x)\bigr)=\sqrt[3]{\text{sen}(x) +x } \ \longrightarrow \ f'\bigl(g(x)\bigr)= \cfrac{1}{3\sqrt[3]{\bigl(\text{sen}(x) +x\bigr)^2 }}

Und nun leiten wir das Argument aus dem Radikal ab. Da es sich um eine Summe von Funktionen handelt, ist die Ableitung die Summe der Ableitungen jedes Termes:

g(x)=\text{sen}(x) +x \ \longrightarrow \ g'(x)=\cos(x) + 1

Somit ist die Ableitung der gesamten Funktion gleich der Multiplikation der beiden berechneten Ableitungen:

z(x)=f\bigl(g(x)\bigr) \ \longrightarrow \ z'(x)=f'\bigl(g(x)\bigr)\cdot g'(x)

\begin{aligned}f(x)=\sqrt[3]{\text{sen}(x)+x} \ \longrightarrow \ f'(x)& = \cfrac{1}{3\sqrt[3]{\bigl(\text{sen}(x) +x\bigr)^2 }} \cdot \bigl(\cos(x) + 1 \bigr)\\[1.5ex]&=\cfrac{\bm{\cos(x) + 1}}{\bm{3\sqrt[3]{\bigl(\mathbf{sen}(x) +x\bigr)^2} }}\end{aligned}

Übung 5

Leiten Sie mithilfe der Kettenregel die folgende Zusammensetzung von Funktionen her:

f(x)=3^{x^2+5}

Um die Kettenregel anzuwenden, müssen Sie die Ableitung der Potenz und des Polynoms ermitteln und diese dann multiplizieren. Daher leiten wir die Leistung mithilfe der entsprechenden Formel ab:

f(x)=a^x \ \longrightarrow \ f'(x)=a^x\cdot \ln (a)

f\bigl(g(x)\bigr)=3^{x^2+5} \ \longrightarrow \ f'\bigl(g(x)\bigr)= 3^{x^2+5}\cdot \ln(3)

Zweitens leiten wir die Polynomfunktion aus dem Exponenten ab:

g(x)=x^2+5 \ \longrightarrow \ g'(x)=2x

Und die Kettenregel sagt uns, dass die Ableitung der gesamten Funktion das Produkt der Ableitungen ist, die wir gerade gefunden haben:

z(x)=f\bigl(g(x)\bigr) \ \longrightarrow \ z'(x)=f'\bigl(g(x)\bigr)\cdot g'(x)

f(x)=3^{x^2+5} \ \longrightarrow \ \bm{f'(x)= 3^{x^2+5}\cdot \ln(3) \cdot 2x}

Übung 6

f(x)=\ln \bigl(4x^2 \cdot \cos(x) \bigr)

Offensichtlich ist die Funktion in diesem Problem zusammengesetzt, da wir im Argument des natürlichen Logarithmus ein Produkt aus zwei verschiedenen Arten von Funktionen haben. Wir differenzieren also zunächst den Logarithmus:

f(x)=\ln(x) \ \longrightarrow \ f'(x)=\cfrac{1}{x}

f\bigl(g(x)\bigr)=\ln \bigl(4x^2 \cdot \cos(x) \bigr) \ \longrightarrow \ f'\bigl(g(x)\bigr)= \cfrac{1}{4x^2 \cdot \cos(x) }

Zweitens leiten wir die Funktion aus dem Logarithmusargument ab. Da es sich um eine Multiplikation zweier Funktionen handelt, müssen Sie zur Ableitung die folgende Formel verwenden:

z(x)=f(x) \cdot g(x) \ \longrightarrow \ z'(x)=f'(x)\cdot g(x)+f(x) \cdot g'(x)

\begin{aligned}g(x)=4x^2 \cdot \cos(x) \ \longrightarrow \ g'(x) & = 8x\cdot \cos(x) + 4x^2 \cdot \bigl(- \text{sen}(x)\bigr) \\[2ex] & = 8x\cdot \cos(x) - 4x^2 \cdot \text{sen}(x)\end{aligned}

Somit ist die Ableitung der gesamten Funktion gemäß der Kettenregel das Produkt der beiden Ableitungen:

z(x)=f\bigl(g(x)\bigr) \ \longrightarrow \ z'(x)=f'\bigl(g(x)\bigr)\cdot g'(x)

\begin{aligned}f'(x)&= \cfrac{1}{4x^2 \cdot \cos(x) } \cdot \bigl( 8x\cdot \cos(x) - 4x^2 \cdot \text{sen}(x) \bigr)\\[1.5ex]&=\cfrac{8x\cdot \cos(x) - 4x^2 \cdot\text{sen}(x)}{4x^2 \cdot \cos(x)}\\[1.5ex]&=\cfrac{\bm{2\cos(x) - x \cdot }\mathbf{sen}\bm{(x)}}{\bm{x \cdot \cos(x) }}\end{aligned}

Übung 7

Lösen Sie die Ableitung der folgenden Funktion mithilfe der Kettenregel:

f(x)=\log_9 (e^{x^2}-6x^7)

Da es sich um eine Zusammensetzung von Funktionen handelt, werden wir den Logarithmus und sein Argument separat differenzieren und dann die Ableitungen multiplizieren.

Also differenzieren wir zunächst den Logarithmus zur Basis 9:

f(x)=\log_a (x) \ \longrightarrow \ f'(x)=\cfrac{1}{x\cdot \ln (a)}

f\bigl(g(x)\bigr)=\log_9 (e^{x^2}-6x^7) \ \longrightarrow \ f'\bigl(g(x)\bigr)=\cfrac{1}{\bigl(e^{x^2}-6x^7\bigr)\cdot \ln(9)}

Und jetzt berechnen wir die Ableitung des Arguments des Logarithmus. Beachten Sie, dass die Zahl e eine Funktion in ihrem Argument hat, d. h. es ist eine zusammengesetzte Funktion, daher müssen wir auch die Kettenregel anwenden, um diese Funktion abzuleiten:

z(x)=f\bigl(g(x)\bigr) \ \longrightarrow \ z'(x)=f'\bigl(g(x)\bigr)\cdot g'(x)

h(x)=e^{x^2} \ \longrightarrow \ h'(x)=e^{x^2}\cdot \bigl(x^2\bigr)' =e^{x^2}\cdot 2x

Somit ist die Ableitung des ganzzahligen Arguments des Logarithmus:

g(x)= e^{x^2}-6x^7\ \longrightarrow \ g'(x)=e^{x^2}\cdot 2x - 42x^6

Und schließlich ist die Ableitung der gesamten Funktion das Produkt von f'(g(x)) und g'(x):

z(x)=f\bigl(g(x)\bigr) \ \longrightarrow \ z'(x)=f'\bigl(g(x)\bigr)\cdot g'(x)

\begin{aligned}f'(x)&=\cfrac{1}{\bigl(e^{x^2}-6x^7\bigr)\cdot \ln(9)} \cdot \bigl(e^{x^2}\cdot 2x - 42x^6\bigr)\\[1.5ex]&=\cfrac{\bm{e^{x^2}\cdot 2x - 42x^6}}{\bm{\bigl(e^{x^2}-6x^7\bigr)\cdot \ln(9)}}\end{aligned}

Übung 8

Leiten Sie die folgende zusammengesetzte Funktion mithilfe der Kettenregel ab:

f(x)=\text{sen}\biggl( \Bigl(9x^5 + \cos(x) \Bigr)^2 \biggr)

Da wir in dieser Übung eine Komposition aus mehreren Funktionen haben, müssen wir die Kettenregel mehrmals anwenden. Wir leiten zunächst die trigonometrische Funktion vom Sinus ab, dessen Ableitung der Cosinus ist:

f\bigl(g(x)\bigr)=\text{sen}\biggl( \Bigl(9x^5 + \cos(x) \Bigr)^2 \biggr)\ \longrightarrow \ f'\bigl(g(x)\bigr)=\cos\biggl( \Bigl(9x^5 + \cos(x) \Bigr)^2 \biggr)

Und jetzt berechnen wir die Ableitung des Sinusarguments mithilfe der Kettenregel:

z(x)=f\bigl(g(x)\bigr) \ \longrightarrow \ z'(x)=f'\bigl(g(x)\bigr)\cdot g'(x)

\begin{aligned} g(x)= \Bigl( 9x^5 + \cos(x) \Bigr)^2 \cdot g'(x) &= 2\Bigl(9x^5 + \cos(x) \Bigr) \cdot \Bigl(9x^5 + \cos(x) \Bigr)' \\[1.5ex]&=2\Bigl(9x^5 + \cos(x) \Bigr) \cdot \Bigl(45x^4-\text{sen}(x)\Bigr)\end{aligned}

Schließlich erhalten wir die Ableitung der gesamten Funktionszusammensetzung, indem wir erneut die Kettenregel anwenden:

z(x)=f\bigl(g(x)\bigr) \ \longrightarrow \ z'(x)=f'\bigl(g(x)\bigr)\cdot g'(x)

\bm{f'(x)=\cos } \bm{\biggl( \Bigl(9x^5 + \cos(x) \Bigr)^2 \biggr) \cdot 2\Bigl(9x^5 + \cos(x) \Bigr) \cdot \Bigl(45x^4-}\mathbf{sen}\bm{(x)\Bigr)}

Kettenregelbeweis

Abschließend beweisen wir die Kettenregelformel. Dazu gehen wir von der mathematischen Definition einer Ableitung aus:

\displaystyle f'(x)=\lim_{h \to 0}\frac{f(x+h)-f(x)}{h}

Sei z eine Funktion, die aus zwei Funktionen besteht:

z=f\bigl(g(x)\bigr)

Dann wäre die Ableitung der Funktion z unter Anwendung der Definition:

\displaystyle z'(x)=\lim_{h \to 0}\frac{f\bigl(g(x+h)\bigr)-f\bigl(g(x)\bigr)}{h}

Wie Sie bereits wissen, können Sie einen Bruch mit demselben Term multiplizieren und dividieren, da sich dadurch das Ergebnis nicht ändert. Wir können also zum nächsten Schritt übergehen:

\displaystyle z'(x)=\lim_{h \to 0}\frac{f\bigl(g(x+h)\bigr)-f\bigl(g(x)\bigr)}{h}\cdot \frac{g(x+h)-g(x)}{g(x+h)-g(x)}

Wir ordnen die Nenner der Brüche neu:

\displaystyle z'(x)=\lim_{h \to 0}\frac{f\bigl(g(x+h)\bigr)-f\bigl(g(x)\bigr)}{g(x+h)-g(x)}\cdot \frac{g(x+h)-g(x)}{h}

Indem wir die Eigenschaften von Grenzwerten anwenden, können wir den obigen Grenzwert in zwei Teile aufteilen. Da der Grenzwert eines Produkts gleich dem Produkt der Grenzwerte ist:

\displaystyle z'(x)=\lim_{h \to 0}\frac{f\bigl(g(x+h)\bigr)-f\bigl(g(x)\bigr)}{g(x+h)-g(x)}\cdot \lim_{h \to 0}\frac{g(x+h)-g(x)}{h}

Und dieser Ausdruck entspricht dem Folgenden:

\displaystyle z'(x)=f'\bigl(g(x)\bigr)\cdot g'(x)

Die Kettenregelformel ist somit bewiesen, da wir aus der Definition der Ableitung zu ihr gelangt sind.

Kommentar verfassen

Deine E-Mail-Adresse wird nicht veröffentlicht. Erforderliche Felder sind mit * markiert

Nach oben scrollen