Es ist sehr üblich, Funktionen darzustellen, um die Beziehung zwischen den verschiedenen Variablen, aus denen diese Funktion besteht, grafisch analysieren zu können. Manchmal werden diese Arten von Darstellungen sogar zum Erwerb mehrerer Funktionen verwendet. Dies kommt insbesondere bei der Durchführung statistischer Untersuchungen zum Einsatz. Vor diesem Hintergrund erklären wir Ihnen heute eine sehr einfache Methode, die nur aus drei Schritten besteht, um jede Funktion grafisch darstellen zu können. Darüber hinaus besprechen wir auch, wie man das grafische Ergebnis analysiert, um Schlussfolgerungen zu ziehen.
Arten von Funktionen
Zunächst müssen wir die Eigenschaften verschiedener Arten von Funktionen verstehen und wissen, welche Unterschiede bei deren Darstellung berücksichtigt werden sollten. Auf diese Weise wird es uns leichter fallen, die grafische Darstellung durchzuführen, weshalb wir nun zu jedem Typ kurz Stellung nehmen. Es ist erwähnenswert, dass es viele Arten von Funktionen gibt. Daher konzentrieren wir uns auf die beiden wichtigsten Arten von Polynomfunktionen und stückweisen Funktionen.
lineare Funktionen
Die lineare Funktion oder Polynomfunktion ersten Grades ist die Funktion, deren Ausdruck ein Polynom vom Grad 1 ist. Dann folgt ihr Ausdruck dem Modell f(x) = mx + n , wobei m die Steigung und n die Ordinate ist. Grundsätzlich haben diese Funktionen eine grafische Form, die einer Linie entspricht. Nachfolgend sehen Sie ein Beispiel:
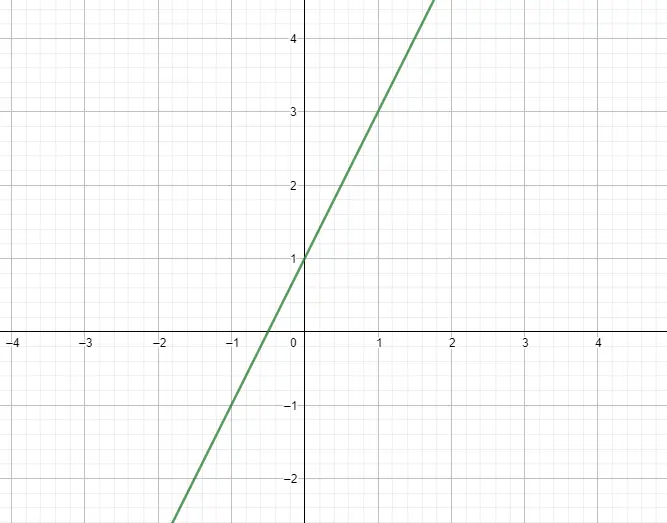
quadratische Funktionen
Die quadratische Funktion oder parabolische Funktion wird durch ein Polynom zweiten Grades ausgedrückt und hat daher eine parabolische Form. Als zu befolgendes Modell berücksichtigen wir den folgenden Ausdruck: f(x) = ax² + bx + c, wobei a ≠ 0. Außerdem gibt es zwei weitere bemerkenswerte Eigenschaften dieser Funktionen, Amplitude und Wachstum. Nachfolgend sehen Sie ein Beispiel:
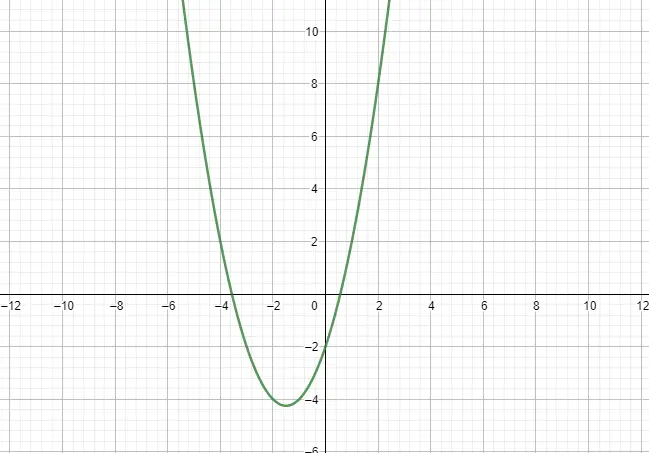
Stückweise Funktionen
Eine stückweise definierte Funktion ist eine Funktion, die abhängig vom Wert von x unterschiedliche Definitionen hat. Wenn x also einen bestimmten Wertebereich einnimmt, müssen wir einen Ausdruck ausprobieren. Wenn das x hingegen andere Werte einnimmt, muss ein anderer Ausdruck verarbeitet werden. Hier finden wir Diskontinuitäten und damit Grenzen. Denn wo eine Funktion endet, kann eine andere beginnen, jedoch ohne direkte Verbindung. Nachfolgend sehen Sie ein Beispiel:
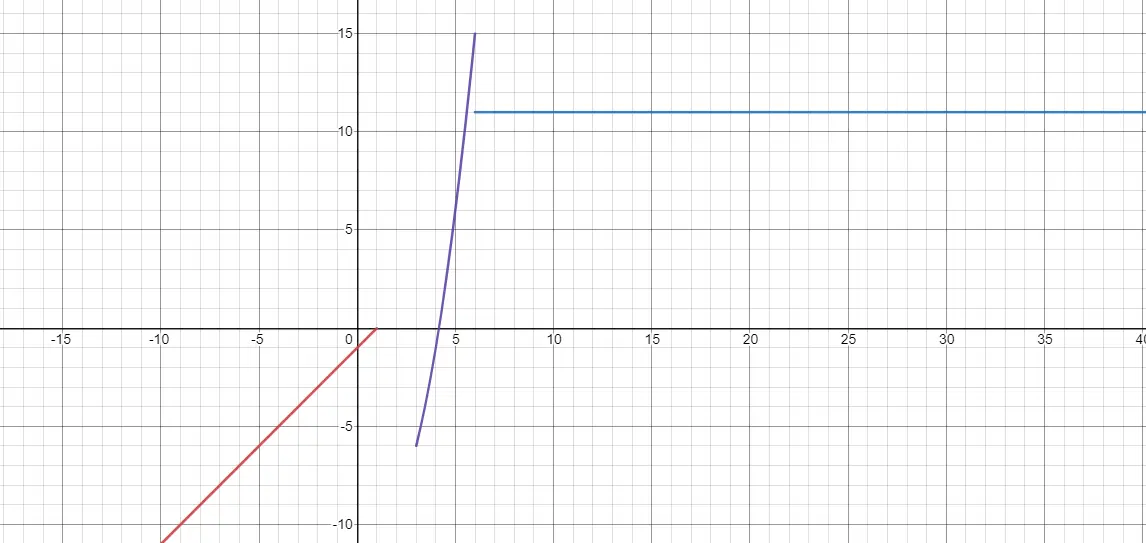
Wie stellt man lineare Funktionen dar?
Um eine lineare Funktion grafisch darzustellen, müssen wir drei sehr einfache Schritte befolgen. Als nächstes erklären wir das Verfahren. Wenn Sie jedoch lernen möchten, wie man Parabelfunktionen grafisch darstellt, empfehlen wir Ihnen, den nächsten Abschnitt zu lesen.
Erstellen Sie eine Wertetabelle
Um eine Funktion grafisch darstellen zu können, müssen wir eine Wertetabelle erstellen, in die wir alle Werte der Variablen schreiben. Im Grunde können wir so eine Beziehung zwischen den beiden Variablen herstellen und auf diese Weise den Verlauf der Funktion nachvollziehen. Wenn Sie nicht wissen, wie man eine Wertetabelle erstellt, können Sie sich diesen letzten Link ansehen. Obwohl es zusammenfassend darin besteht, der unabhängigen Variablen einen Wert zuzuweisen und das Unbekannte in die Funktion zu ersetzen, die sich auf sie bezieht. Damit wir die beiden zugehörigen Zahlen haben, zeigt die folgende Tabelle ein Beispiel:
Aus der Funktion f(x) = 2x+1:
| X | f(x) |
| 0 | 1 |
| 1 | 3 |
| 2 | 5 |
| 3 | 7 |
Zeichnen Sie Punkte im Diagramm und verbinden Sie sie durch Zeichnen der Funktion
Sobald wir die Tabelle erstellt haben, können wir mit dem Zeichnen der Punkte in einem Diagramm beginnen. Dazu verknüpfen wir die unabhängige Variable mit der x-Achse und die andere mit der y-Achse und erhalten so die Punkte. Sie können so viele Punkte zeichnen, wie Sie möchten. Um Funktionen dieses Stils darzustellen, reicht es jedoch normalerweise aus, fünf Punkte zu berechnen. Seitdem sind sie einem geraden Weg gefolgt und daher bleibt dieser immer derselbe, egal wie weit man voranschreitet.
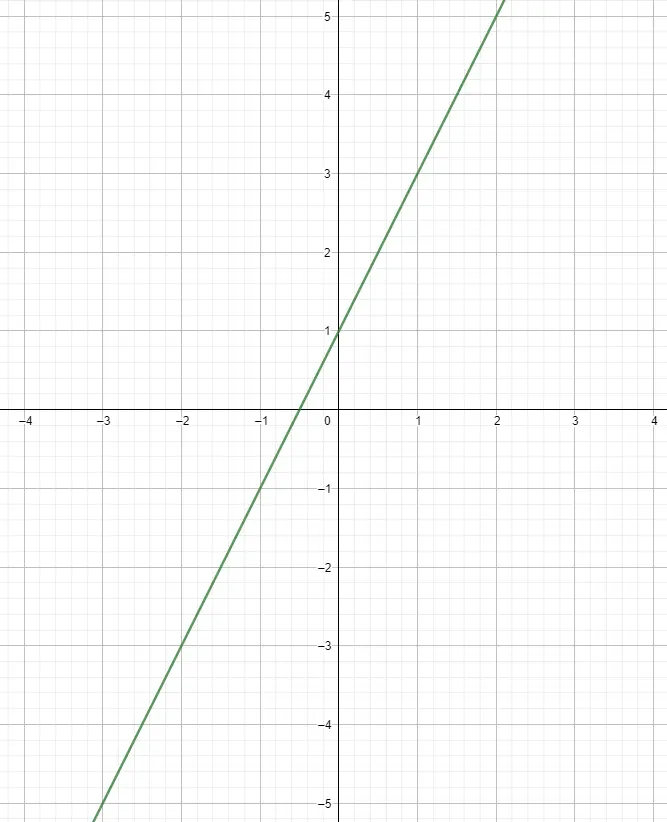
Verwenden der Steigung zur grafischen Darstellung einer linearen Funktion
Um lineare Funktionen ohne Wertetabellen grafisch darstellen zu können, gibt es eine zweite Methode, die darin besteht, die Steigung der Funktion zu berechnen: m = (vertikale Variation / horizontale Variation). Nachdem wir also die Steigung berechnet haben, müssen wir uns den Ausgangspunkt ansehen. Zurück zum vorherigen Beispiel f(x) = 2x+1: Wir wissen, dass der Ausgangspunkt (0, 1) sein wird, da bei x = 0 der Computer = 1 ist (wir leiten es aus der +1 im Ausdruck ab). . Und dann addieren Sie einfach die Neigung, die in diesem Fall +2 Vertikale für 1 Horizontale beträgt. Dann wissen wir, dass der nächste Punkt (1,3) sein wird.
Wie stellt man quadratische Funktionen dar?
Um eine quadratische Funktion darzustellen, können wir zwei Methoden anwenden: Die erste umfasst Wertetabellen. Und die zweite besteht darin, eine Reihe von Schlüsselpunkten zu berechnen: den Scheitelpunkt, die Schnittpunkte mit der X-Achse und den Schnittpunkt mit der Y-Achse. Letzteres ist das, was wir im Folgenden erklären werden:
Berechnen Sie den Scheitelpunkt einer Parabel
Es gibt zwei Formeln, mit denen wir den Scheitelpunkt einer Parabelfunktion berechnen können. Grundsätzlich gibt uns die eine den Scheitelpunkt der X-Achse und die andere den Scheitelpunkt der Y-Achse. Beide Formeln finden Sie unten, beide haben jedoch einen ähnlichen Aufbau.
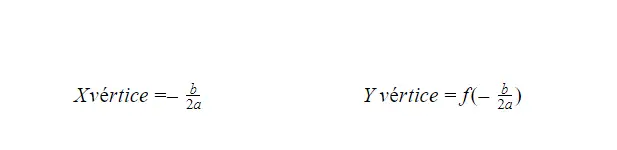
Berechnen Sie die Schnittpunkte mit der X-Achse einer quadratischen Funktion
Um die Schnittpunkte von zu erhalten, müssen wir lediglich die Gleichung lösen und schon haben wir die Werte von X, die wir suchen. Es ist erwähnenswert, dass wir als quadratische Funktion zwei Ergebnisse erhalten, nicht nur eines.
Berechnen Sie den Schnittpunkt mit der Y-Achse einer quadratischen Funktion
Um schließlich den Schnittpunkt mit der Y-Achse zu erhalten, berechnen Sie einfach c = f(0). Und da eine Parabel immer die vertikale Achse (Ordinate) schneidet, wenn x = 0 ist, dann sagen wir, dass der Schnittpunkt der Y-Achse (0,c) ist. Sobald wir alle diese Punkte haben, können wir sie in die Grafik einzeichnen und müssen sie nur noch verbinden, indem wir die Parabel wie folgt zeichnen.
Wie stellt man Funktionen stückweise dar?
Um Funktionen in Teilen darstellen zu können, können Sie alle zuvor erläuterten Methoden kombinieren. Da Funktionen dieses Stils aus allen Arten von Funktionen bestehen, über die wir gesprochen haben. Daher gibt es einige, die Sie anhand einer Wertetabelle berechnen müssen, und andere, die Sie mit anderen Methoden berechnen müssen. Sobald Sie jedoch die in diesem Artikel erläuterten Funktionen beherrschen, werden Sie bei der Darstellung von Funktionen in Teilen keine Probleme mehr haben.
Da Sie andererseits bei deren Darstellung eine Kontinuitätsstudie durchführen müssen, empfehlen wir Ihnen, zu lernen, wie Sie die Grenzen auflösen können, falls Sie noch nicht wissen, wie. Dies wird Ihnen helfen, die Endpunkte jeder Funktion korrekt darzustellen. Damit sind Sie nun bereit, stückweise Funktionen und jede andere Art von Funktion grafisch darzustellen. Wir geben Ihnen nun eine Reihe von Grafiktipps und eine sehr nützliche Erklärung der Fähigkeit des Taschenrechners, Grafiken zu erstellen.
Wie erstellt man Grafiken mit dem Taschenrechner?
Wenn Sie über einen Grafikrechner verfügen, kann dieser grafisch darstellen. Dies kann sehr einfach sein, wenn Sie die Vorgehensweise kennen. Wenn Sie jedoch immer noch nicht wissen, wie es geht, erklären wir es Ihnen jetzt.
- Auf den Grafikmodus zugreifen: Der erste Schritt besteht darin, über das Menü auf die Option „Grafiken“ oder „grafische Darstellungen“ zuzugreifen. Diese Option ist möglicherweise mit einem anderen Namen für Ihren Taschenrechner gekennzeichnet, enthält jedoch Wörter, die der Grafik ähneln oder über die wir bereits gesprochen haben.
- Passen Sie die Diagrammoptionen an: Sobald wir uns im Diagrammeditor befinden, müssen wir der Datei einen Namen geben, die Achsen beschriften, die Anzahl der Elemente auswählen, die grafisch dargestellt werden sollen, und die ästhetischen Optionen der Darstellung konfigurieren. Dies ist ein sehr schneller Schritt.
- Fügen Sie die Punkte der Funktion hinzu: Sie können dann mit dem Hinzufügen der Punkte beginnen, die die Figur bilden. Sie können dies tun, indem Sie die Punkte mit der folgenden Notation schreiben: (0,1), (3,2)… Und Sie werden die Punkte so lange hinzufügen, bis Sie mit der grafischen Darstellung fertig sind.
- Nutzen Sie die Funktion „Vorschau“: Sobald Sie das Projekt abgeschlossen haben, können Sie eine Vorschau des Ergebnisses anzeigen und sehen, ob es wie erwartet ausfällt. Darüber hinaus verfügen viele Vorlagen mit dieser Vorschau über Bearbeitungsoptionen, sodass Sie das Ergebnis optimieren können, bis es perfekt ist.
- Speichern Sie das Projekt: Wenn der gesamte Bearbeitungsvorgang abgeschlossen ist, denken Sie daran, es an einem leicht zu merkenden Ort zu speichern. Auf diese Weise können Sie bei Bedarf jederzeit wieder auf das Projekt zugreifen, um es anzuzeigen oder die gewünschten Verbesserungen vorzunehmen.
Beste Rechner zur Darstellung von Funktionen
Wenn Sie sich für den Kauf eines Grafikmodells interessieren, um Funktionen auf demselben Rechner darstellen zu können, empfehlen wir Ihnen zwei Modelle: den HP 50G und den HP Prime . Dies sind zwei der hochwertigsten Modelle, obwohl sie teuer sind. Sie müssen sich also fragen, ob sich die Investition für Sie lohnt. Wenn Sie beispielsweise einen mathematisch sehr komplexen Beruf wie den Ingenieursberuf studieren möchten, ist die Anschaffung eines dieser beiden Modelle sehr zu empfehlen. Wenn Sie jedoch nicht so viel Rechen- oder Grafikleistung benötigen, ist der Casio FX-9750GII möglicherweise ausreichend für Sie.
Wie kann man Funktionen online grafisch darstellen?
Sie können jederzeit die Möglichkeit wählen, Online-Grafikprogramme wie Desmos , Geogebra und viele andere zu verwenden. Auf diese Weise erhalten Sie schnell sehr genaue Grafiken. Wir können sagen, dass die Zahlenform verwendet wird, wenn Sie Funktionen einfach und schnell grafisch darstellen möchten. Wenn Sie andererseits Funktionen grafisch darstellen möchten, damit Sie sie bearbeiten (alle ihre Attribute ändern) können und hochwertige Ressourcen zur Funktionsanalyse zur Hand haben, empfehlen wir den Kauf eines wissenschaftlichen Taschenrechners.