Auf dieser Seite wird erklärt, was eine quadratische Funktion ist und welche Eigenschaften sie hat: Krümmung, Scheitelpunkt, Schnittpunkte mit den Achsen usw. Außerdem erfahren Sie, wie Sie eine quadratische Funktion in einem Diagramm darstellen. Und schließlich können Sie mit Beispielen, Schritt-für-Schritt-Übungen und Problemen zu quadratischen Funktionen üben.
Was ist eine quadratische Funktion?
Die Definition einer quadratischen Funktion lautet wie folgt:
In der Mathematik ist eine quadratische (oder parabolische) Funktion eine Polynomfunktion vom Grad 2, also eine Funktion, bei der der Term höchster Ordnung vom zweiten Grad ist. Daher lautet die Formel für eine quadratische Funktion:
![]()
Gold:
-
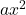
ist der quadratische Term.
-
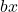
ist der lineare Term.
-

ist der unabhängige Begriff.
Der Definitionsbereich einer quadratischen Funktion besteht immer aus reellen Zahlen.
![]()
Konkavität und Konvexität einer quadratischen Funktion
Die Analyse der Krümmung einer quadratischen oder parabolischen Funktion ist sehr einfach, da sie nur vom quadratischen Koeffizienten abhängt.
- Wenn der Koeffizient

positiv ist, ist die quadratische Funktion konvex (in der Form

). Der Gipfel ist also ein Minimum.
- Wenn der Koeffizient

negativ ist, ist die quadratische Funktion konkav (geformt wie

). Der Peak ist also ein Maximum.


Hinweis: Die mathematische Gemeinschaft ist sich immer noch nicht ganz einig und daher sagen einige Professoren das Gegenteil: Sie nennen eine Funktion konkav, wenn sie die Form eines a hat
![]()
und eine konvexe Funktion, die die Form hat
![]()
. Wichtig ist in jedem Fall, welche Form die Funktion hat, egal wie der Name lautet.
Scheitelpunkt einer quadratischen Funktion
Um eine quadratische Funktion grafisch darzustellen, müssen die Koordinaten des Scheitelpunkts der Parabel bekannt sein.
Um den Scheitelpunkt einer quadratischen Funktion zu finden, müssen wir die X-Koordinate des Punktes mit der folgenden Formel berechnen:
![]()
Dann können wir die andere Scheitelpunktkoordinate ermitteln, indem wir das Bild der Funktion an diesem Punkt berechnen:
![]()
Somit sind die Koordinaten des Scheitelpunkts einer quadratischen Funktion (oder Parabel):
![]()
Schnittpunkte mit den Achsen einer quadratischen Funktion
Eine Parabel schneidet immer die y-Achse (Y-Achse), und das passiert, wenn
![]()
Um den Cutoff-Punkt einer quadratischen Funktion mit der Y-Achse zu berechnen, muss man daher lösen
![]()
Der Schnittpunkt der folgenden quadratischen Funktion mit der OY-Achse ist beispielsweise:
![]()
![]()
![]()
Andererseits liegt der Grenzpunkt einer quadratischen Funktion mit der x-Achse (X-Achse) bei
![]()
Um den Schnittpunkt mit der X-Achse zu berechnen, müssen Sie die Gleichung lösen
![]()
Nachfolgend finden Sie als Beispiel die Berechnung des Grenzwerts mit der OX-Achse derselben quadratischen Funktion:
![]()
![]()
Wir lösen die quadratische Gleichung mit der allgemeinen Formel:
![]()
![]()
Der Schnittpunkt der quadratischen Funktion mit der X-Achse ist also:
![]()
In diesem Fall haben wir nur eine Lösung für die quadratische Gleichung erhalten, wir hätten aber auch zwei Lösungen erhalten können. Das bedeutet in diesem Fall, dass die quadratische Funktion die X-Achse in zwei verschiedenen Punkten schneidet.
Beispiel für die Darstellung einer quadratischen oder parabolischen Funktion
Sehen wir uns anhand eines Beispiels an , wie man eine quadratische Funktion in einem Diagramm darstellt .
- Stellen Sie die folgende Funktion grafisch dar:
![]()
Als erstes muss der Scheitelpunkt der Parabel berechnet werden. Dazu verwenden wir die Formel, die wir oben gesehen haben:
![]()
Sobald wir wissen, wo der Scheitelpunkt sein wird, müssen wir eine Wertetabelle erstellen: Wir berechnen den Wert der Funktion am Scheitelpunkt und an den ihn umgebenden Punkten:
![]()
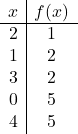
Sie können die Schnittpunkte der quadratischen Funktion auch mit den kartesischen Achsen berechnen, um die Parabel besser zeichnen zu können, dies ist jedoch nicht unbedingt erforderlich.
Wir stellen nun die erhaltenen Punkte grafisch dar :
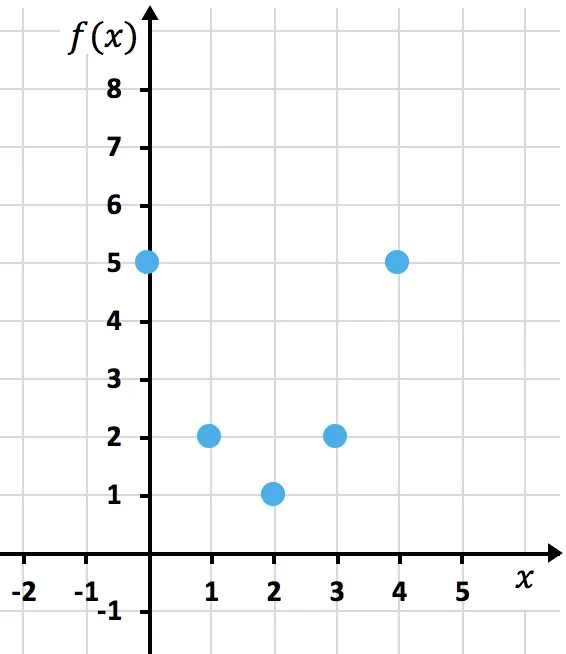
Und schließlich verbinden wir die Punkte zu einer Parabel. Dann verlängern wir die Äste der Parabel, um anzuzeigen, dass sie sich nach oben fortsetzt:

Gelöste Übungen zu quadratischen Funktionen
Übung 1
Finden Sie den Scheitelpunkt der folgenden quadratischen Funktion:
![]()
Wir berechnen zunächst die X-Koordinate des Scheitelpunkts mit der Formel:
![]()
Und jetzt berechnen wir die andere Koordinate, indem wir die Funktion am Punkt auswerten:
![Rendered by QuickLaTeX.com \begin{aligned} f(-2) & =2(-2)^2+8(-2)+4 \\[1.7ex] & = 2 \cdot 4 - 16 +4 \\[1.7ex] & = 8-16+4 \\[1.7ex] & = -4 \end{aligned}](https://mathority.org/wp-content/ql-cache/quicklatex.com-d6067325564a5af06f7384d76157f3aa_l3.png)
Der Scheitelpunkt der quadratischen Funktion ist daher:
![]()
Übung 2
Finden Sie die Grenzwerte der folgenden Funktion mit den Achsen:
![]()
Um den Schnittpunkt mit der Y-Achse zu berechnen, müssen wir berechnen
![]()
![]()
Die Funktion verläuft also durch die Y-Achse im Punkt:
![]()
Und um die Schnittpunkte mit der X-Achse zu finden, müssen wir lösen
![]()
![]()
![]()
Wir berechnen die Wurzeln der quadratischen Gleichung mit der Formel:
![]()
![Rendered by QuickLaTeX.com \displaystyle x=\cfrac{-(-4)\pm \sqrt{(-4)^2-4\cdot 1\cdot 3}}{2\cdot 1} =\cfrac{4\pm 2}{2} = \begin{cases} 3 \\[2ex] 1 \end{cases}](https://mathority.org/wp-content/ql-cache/quicklatex.com-0d909ba6581faf5916f0b1c0df7e471f_l3.png)
Die Funktion schneidet daher die X-Achse an zwei Punkten:
![]()
Übung 3
Stellen Sie die folgende quadratische Funktion grafisch dar:
![]()
Dies ist eine quadratische Funktion. Um es darzustellen, müssen Sie daher zunächst die Abszisse des Scheitelpunkts der Parabel mit der Formel berechnen:
![]()
Jetzt erstellen wir die Wertetabelle. Dazu berechnen wir den Wert von
![]()
oben und rundherum:
![]()
![]()
![]()
![]()
![]()
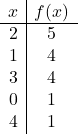
Und schließlich tragen wir die Punkte im Diagramm ein und zeichnen die Parabel:

Übung 4
Stellen Sie die folgende quadratische Funktion grafisch dar:
![]()
Dies ist eine Funktion zweiter Ordnung. Um es darzustellen, müssen Sie daher zunächst die Abszisse des Scheitelpunkts der Parabel mit der Formel ermitteln:
![]()
Jetzt erstellen wir die Wertetabelle. Dazu berechnen wir den Wert von
![]()
oben und rundherum:
![]()
![]()
![]()
![]()
![]()

Zum Schluss tragen wir die Punkte im Diagramm ein und zeichnen die Parabel:

Übung 5
Zeichnen Sie die folgende unvollständige quadratische Funktion in ein Diagramm:
![]()
Es handelt sich um eine Polynomfunktion zweiten Grades. Um es darzustellen, müssen Sie daher zunächst die Abszisse des Scheitelpunkts der Parabel mit der Formel berechnen:
![]()
In diesem Fall ist die Funktion unvollständig, da sie keinen Term ersten Grades hat. Dafür
![]()
Jetzt erstellen wir die Wertetabelle. Dazu berechnen wir den Wert von
![]()
oben und rundherum:
![]()
![]()
![]()
![]()
![]()

Zum Schluss tragen wir die Punkte im Diagramm ein und zeichnen die Parabel:

Übung 6
Lösen Sie das folgende Problem im Zusammenhang mit quadratischen Funktionen:
Die Herstellungskosten eines Produkts werden durch die folgende Funktion definiert:
![]()
Gold
![]()
sind die produzierten Einheiten (in Tausend) und
![]()
sind die Produktionskosten der Einheiten (in Tausend Euro).
- Stellt die Produktionskostenfunktion in einem Diagramm dar.
- Bestimmen Sie, wie viele tausend Einheiten produziert werden sollten, um die Kosten zu minimieren.
Dies ist eine quadratische Funktion. Um es darzustellen, müssen Sie daher zunächst die Abszisse des Scheitelpunkts der Parabel mit der Formel ermitteln:
![]()
Jetzt erstellen wir die Wertetabelle. Dazu berechnen wir den Wert von
![]()
oben und rundherum:
![]()
![]()
![]()
![]()
![]()
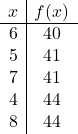
Jetzt tragen wir die Punkte im Diagramm ein und zeichnen die Parabel:
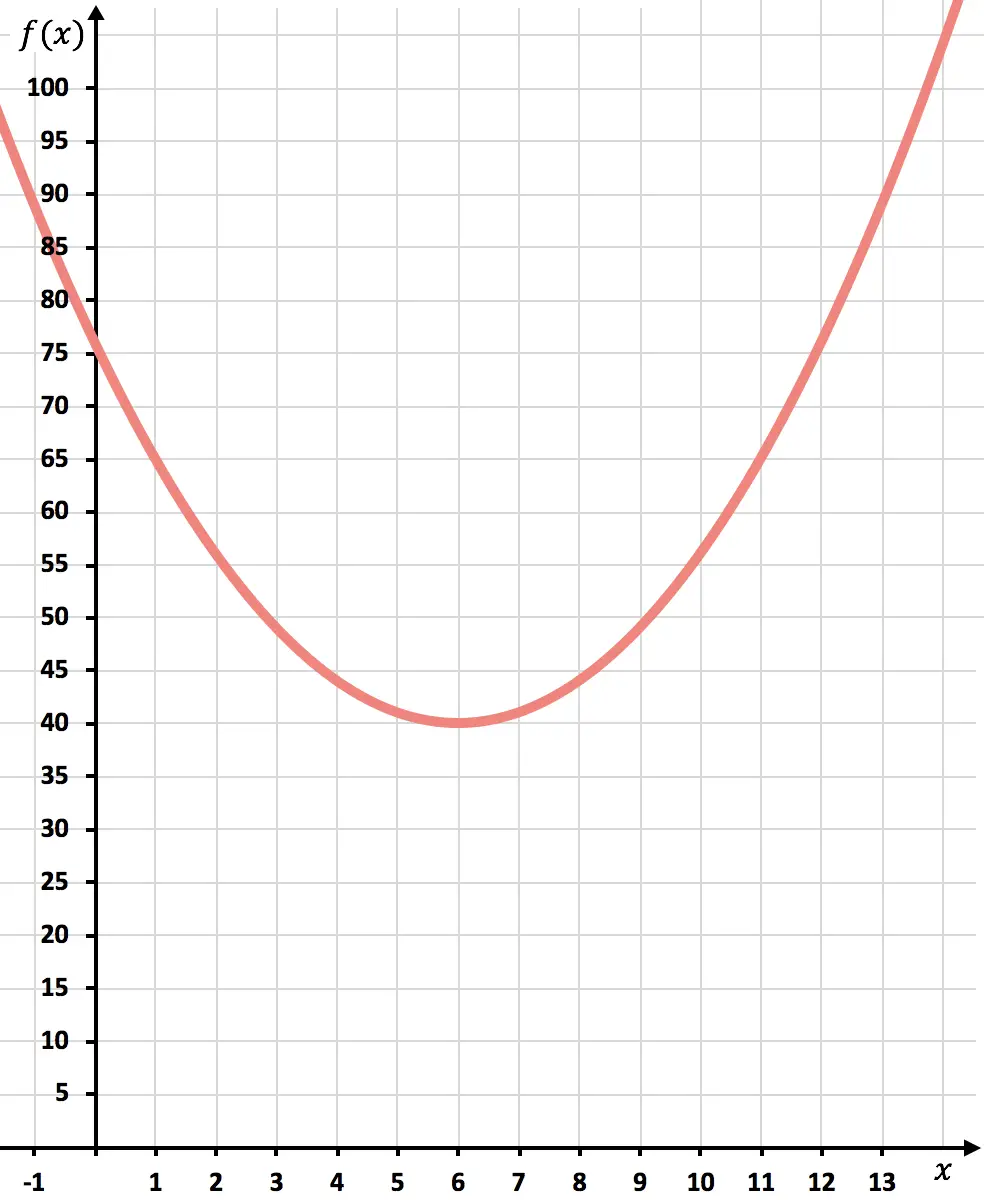
Sobald die Funktion dargestellt ist, werden wir sehen, um wie viel die Kosten minimiert werden.
Wie die Grafik zeigt, werden am oberen Ende der Parabel minimale Kosten erreicht. Denn dort nimmt die Funktion den kleinsten Wert an.
Zusammenfassend lässt sich sagen, dass die Kosten durch die Produktion von 6.000 Einheiten minimiert werden.
Übung 7
Lösen Sie das folgende quadratische Funktionsproblem:
Ein Athlet führt einen Speerwurf aus, dessen Flugbahn durch die folgende Funktion dargestellt werden kann:
![]()
Gold
![]()
sind die vom Speer zurückgelegten Meter und
![]()
seine Höhe (auch in Metern).
Welche maximale Höhe kann der Speer erreichen?
Da es sich um eine quadratische Funktion handelt, ist die Flugbahn des Speers eine Parabel.
Da der Koeffizient des quadratischen Termes außerdem negativ ist (-0,025), hat die Parabel eine umgekehrte U-Form und ihre Zweige verlaufen nach unten. Somit erreicht der Speer oben seine maximale Höhe, da dies der höchste Punkt der Parabel ist.
Wir berechnen daher die Abszisse des Scheitelpunkts der Parabel mit der Formel:
![]()
Und dann berechnen wir, wie hoch der Speer an diesem Punkt sein wird, indem wir die Funktion in auswerten
![]()
![]()
Die maximale Höhe, die der Speerwurf erreichen kann, beträgt daher 42 Meter.
Übung 8
Lösen Sie das folgende Problem bezüglich quadratischer Funktionen:
Die Produktionskosten (in Euro) eines Unternehmens werden durch folgende Funktion definiert:
![]()
Gold
![]()
sind die produzierten Einheiten.
Und der Verkaufspreis pro Einheit beträgt 520 €.
- Wie viel Gewinn wird das Unternehmen erzielen, wenn es 150 Einheiten verkauft?
- Wie viele Einheiten sollten verkauft werden, um den maximalen Gewinn zu erzielen?
Für jede verkaufte Einheit verdient das Unternehmen 520 Euro. Daher ist die Funktion, die das Einkommen definiert:
![]()
Gold
![]()
sind die verkauften Einheiten.
Aber sie fragen uns nach dem Gewinn, also nach Einnahmen minus Kosten. Wir subtrahieren daher Umsatz minus Kosten, um die Funktion zu erhalten, die den Gewinn des Unternehmens beschreibt:
![]()
![]()
![]()
![]()
Sobald wir die Funktion kennen, die den Gewinn des Unternehmens beschreibt, ersetzen Sie einfach 150 in den Funktionsausdruck, um den Gewinn zu berechnen, den das Unternehmen durch den Verkauf von 150 Einheiten erzielen wird:
![Rendered by QuickLaTeX.com \begin{aligned} B(150) & =-(150)^2 + 500\cdot 150 - 40000 \\[2ex] & = -22500+75000 - 40000 \\[2ex] & = \bm{12500} \end{aligned}](https://mathority.org/wp-content/ql-cache/quicklatex.com-9f5e6f3101145bcf1a2ece4db3e07c4e_l3.png)
Beim Verkauf von 150 Einheiten wird das Unternehmen also einen Gewinn von 12.500 € erzielen.
In der Abrechnung werden wir auch aufgefordert, zu berechnen, mit wie vielen Einheiten der maximale Gewinn erzielt wird.
Die Funktion, die den Gewinn beschreibt, ist eine quadratische Funktion und hat daher die Form einer Parabel. Und da der Koeffizient des quadratischen Termes negativ (-1) ist, hat die Parabel eine umgekehrte U-Form und ihre Äste verlaufen nach unten. Daher werden die größten Gewinne an der Spitze erzielt, da dies der höchste Punkt der Parabel ist.
Wir berechnen daher die Abszisse des Scheitelpunkts der Parabel mit der Formel:
![]()
Das Unternehmen wird also durch den Verkauf von 250 Einheiten den maximalen Gewinn erzielen.
Andererseits können wir, auch wenn in der Pressemitteilung nicht danach gefragt wird, den Gewinn ermitteln, der durch den Verkauf dieser 250 Einheiten erzielt wird:
![]()
€