Die Ruffini-Regel ist ein mathematisches Verfahren , das von Paolo Ruffini entwickelt wurde und uns erlaubt, Polynome der Form (x – a) zu dividieren. Diese mathematische Methode wird auch als synthetische Division bezeichnet. Aber wie wird dieses Verfahren angewendet und welche Schritte sind seine Schritte? Und wie löst man eine Ruffini-Übung mit dem Taschenrechner? Das alles erklären wir Ihnen in diesem Artikel zusammengefasst und leicht verständlich , außerdem empfehlen wir Ihnen die besten Rechner für Ruffini.
Ruffini-Rechner online
Wenn Sie ein Polynom faktorisieren möchten, können Sie diesen Rechner verwenden, mit dem Sie jeden Ausdruck faktorisieren können, sofern Sie ihn mit den folgenden Symbolen schreiben: ^ (erhöhen) und / (dividieren). Und Sie können beruhigt sein, denn dieser Rechner ist in der Lage, Polynome vom Grad 3 und noch höheren Graden zu faktorisieren. Es ist daher das ultimative Berechnungstool für die Online-Faktorisierung von Polynomen.
Wie wendet man Ruffini an?
In diesem Abschnitt erklären wir , wie Ruffini durchgeführt wird , und lösen ein konkretes Beispiel mithilfe der Methode. Auf diese Weise können Sie den gesamten Vorgang klar und grafisch sehen. Dadurch können Sie dieses Konzept im Grunde verstehen und sich später in der Prüfung daran erinnern. Zusätzlich haben wir ein Erklärvideo beigefügt, das es Ihnen ermöglicht, dieses Konzept zu verstehen, auch wenn Sie Zweifel an der schriftlichen Erklärung haben.
Voraussetzungen für die Anwendung der Ruffini-Methode
Bevor Sie mit der Lösung einer Division von Polynomen beginnen oder ein Polynom faktorisieren , müssen Sie sich den Divisor ansehen. Handelt es sich um den ersten Grad, können wir mit der Ruffini-Methode fortfahren. Wenn der Divisor hingegen einen Grad größer als 1 hat, können wir die Berechnung nicht mit diesem Verfahren lösen. Daher müssen wir jede andere Methode verwenden, um Polynome zu dividieren. Dies ist ein Faktor, der vor Beginn der Berechnungen überprüft werden muss, da sonst viel Zeit verschwendet werden kann.
Verfahren zur Division von Polynomen mithilfe der Ruffini-Regel
Nachdem wir nun wissen, wann diese mathematische Ressource verwendet werden kann, sehen wir uns die verschiedenen Schritte an, die zu befolgen sind, um ein Polynom zu faktorisieren. Aus dem Beispiel (x³+3x²-1) / (x-2) müssen wir also zunächst die Dividendenkoeffizienten auf eine horizontale Linie schreiben und die fehlenden Terme mit einer Null darstellen. Und dann werden wir den unabhängigen Term des Divisors in das separate Gegenzeichen setzen, wie im Bild gezeigt.
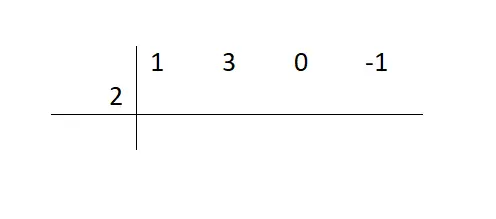
Dann müssen wir den ersten Koeffizienten verringern (denjenigen, der die auf einen höheren Exponenten erhöhte Variable begleitet). Wir werden mit dieser Zahl nichts anfangen, sondern sie reduzieren und mit dem nächsten Schritt fortfahren.
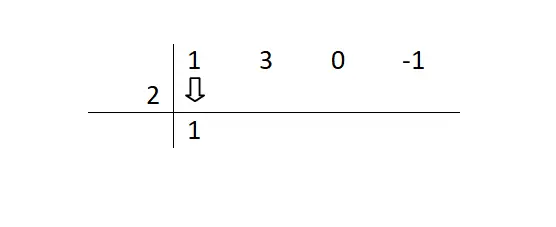
Als nächstes beginnen wir mit einer Reihe sich ziemlich wiederholender Schritte: Wir multiplizieren die Zahl, die wir verringert haben, mit dem Divisor und tragen das Ergebnis unter den nächsten Term ein. Dann fügen wir den nächsten Term zwischen diesem Ergebnis ein und schreiben ihn neben die erste Zahl, die wir notiert haben.
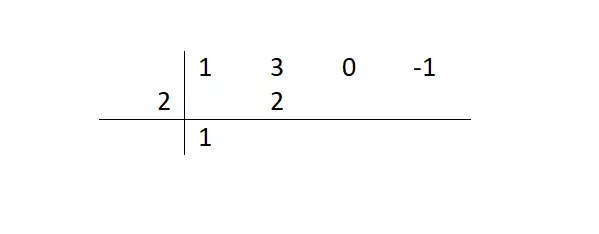
Wenn wir dieser Schrittfolge folgen, bis wir die Tabelle fertiggestellt haben, hätten wir das folgende Layout. Auf diese Weise wissen wir, dass der Rest gleich 19 ist (letzte Zahl, die wir berechnet haben) und dass der Restausdruck (Quotient) x²+5x+10 sein wird. All diese Informationen haben wir den Zahlen in der unteren Reihe entnommen. Und im Fall der Faktorisierung eines Polynoms müssen wir diesen Quotienten verwenden, um weiterhin die anderen Wurzeln zu finden.
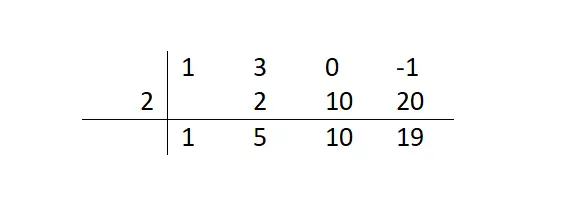
Wie trage ich Ruffini in den Rechner ein?
Um Polynome mit Ruffini auf dem Rechner dividieren zu können, greifen Sie einfach auf die Löser des Rechners zu, also auf den Gleichungsberechnungsmodus. Und sobald wir drin sind, wählen wir die Option „Polynomgleichungen“, weil wir ein Polynom faktorisieren möchten. Dann wählen wir den Grad des Ausdrucks aus und können den mathematischen Editor aufrufen, in dem wir den Ausdruck einführen. Wenn wir also die Wurzeln des Polynoms haben, müssen wir es nur in der Form (x – a) schreiben. Dieses gesamte Verfahren (mit Ausnahme des Wurzelteils) ist identisch mit dem, das wir zum Lösen der Gleichungen mit dem Taschenrechner verwenden werden.
Die besten Rechner zur Berechnung des Ruffini-Theorems
Derzeit gibt es viele Taschenrechner, die Operationen mit Polynomen lösen und faktorisieren können. Allerdings gibt es einige Modelle, die sich durch Benutzerfreundlichkeit und Preis auszeichnen. Zwei gute Beispiele sind das Casio FX-991SPX II und das Casio FX-991ES PLUS . Tatsächlich basiert die Erklärung, die wir im vorherigen Abschnitt gegeben haben, auf der Funktionsweise dieser beiden Modelle. Allerdings gibt es, wie bereits erwähnt, auch andere wissenschaftliche Taschenrechner , mit denen Sie Ruffini perfekt ausführen können.
Ruffini-Beispiele und Übungen
Ruffinis Regel lässt sich praktizieren, indem man zufällig zwei Polynome nimmt, sofern sie den Regeln folgen, die wir zu Beginn kommentiert haben. Mit diesem mathematischen Verfahren können Sie jedoch auch versuchen, Polynome mit einem Grad größer als eins zu faktorisieren. Sie werden also denselben mathematischen Mechanismus und im Gegenzug das Konzept der Wurzel eines Polynoms wiederholen. Als Nächstes zeigen wir Ihnen zwei Polynome, die Sie faktorisieren müssen, und eine ziemlich einfache Division, die Sie mit der Ruffini-Methode lösen müssen.
Übung 1
Faktorisieren Sie das Polynom: 2x³-7x²+8x-3
Wurzeln: x=1 und x=1, wir blieben also bei (x-1)²(2x-3)
Übung 2
Faktorisieren Sie das Polynom: x³+2x²-x-2
Wurzeln: x=-2, x=-1 und x=1, also bliebe (x+2)(x+1)(x-1)
Übung 3
Lösen Sie die folgende Division zwischen Polynomen: (3x³-5x²+2) / (x-2)
Quotient: 3x²+x+2, Rest: 6
Wenn Sie weitere Ruffini-Übungen wünschen, empfehlen wir Ihnen, sich diesen Superprof-Artikel anzusehen, in dem die gleichen Vorgehensweisen wie in diesem Artikel erläutert werden. Aber mit Beispielen und Übungen, die sich ein wenig von denen von Ruffini unterscheiden, können Sie möglicherweise einige Zweifel mit mehr Übung ausräumen. Wie auch immer, wir hoffen, dass Sie unsere Inhalte und den Ruffini-Rechner nützlich fanden.