Linearkombination von Vektoren -

Auf dieser Seite finden Sie die Erklärung, was eine Linearkombination zwischen Vektoren bedeutet. Darüber hinaus können Sie sich ein Beispiel dafür ansehen, wie ein Vektor als Linearkombination dargestellt wird, und außerdem Übungen und Aufgaben lösen, die Schritt für Schritt gelöst werden.

Was ist eine Linearkombination von Vektoren?

Die Definition der Linearkombination lautet wie folgt:

Eine lineare Kombination einer Menge von Vektoren ist der Vektor, der durch Addition aller Vektoren in der Menge multipliziert mit Skalaren (reellen Zahlen) entsteht.

Mit anderen Worten, es ist eine Menge von Vektoren gegeben

$\vv{\text{v}}_1, \vv{\text{v}}_2,\ldots \vv{\text{v}}_n,$

eine Linearkombination davon wäre:

$\vv{\text{w}}=a_1\vv{\text{v}}_1+a_2\vv{\text{v}}_2+\dots + a_n\vv{\text{v}}_n$

Wo die Koeffizienten

$a_i$

Das sind reelle Zahlen.

Daher bedeutet ein Vektor, der eine lineare Kombination anderer Vektoren ist, dass der erste durch den zweiten ausgedrückt werden kann.

Dieses Konzept lässt sich besser verstehen, wenn man einen Vektor in der Ebene grafisch darstellt, der eine lineare Kombination zweier Vektoren ist:

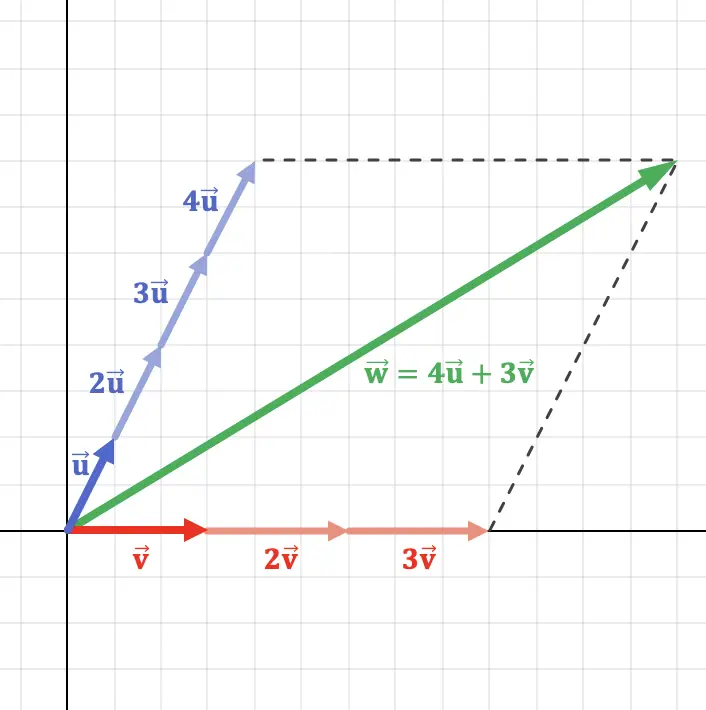
Wie Sie in der grafischen Darstellung oben sehen können, ist der Vektor

$\vv{\text{w}}$

kann aus Vektoren gewonnen werden

$\vv{\text{u}}$

Und

$\vv{\text{v}}$

Vektoroperationen durchführen. Daher der Vektor

$\vv{\text{w}}$

ist eine Linearkombination der beiden anderen Vektoren.

Es sollte betont werden, dass diese lineare Kombination eindeutig ist, oder mit anderen Worten, dass es für jeden Vektor nur eine mögliche lineare Kombination gibt. Da wir, dem vorherigen Beispiel folgend, multipliziert haben

$\vv{\text{u}}$

für 6 statt 4 würden wir einen anderen Vektor erhalten.

Darüber hinaus besteht eine der Eigenschaften der Linearkombination in der Ebene (im R2) darin, dass jeder Vektor als Linearkombination zweier anderer Vektoren dargestellt werden kann, wenn diese unterschiedliche Richtungen haben, also nicht parallel sind.

Manchmal können wir auch mit bloßem Auge erkennen, dass zwei Vektoren eine lineare Kombination sind. Dazu reicht es aus, dass seine Komponenten proportional sind. Beispielsweise sind die Koordinaten der folgenden zwei Vektoren proportional und daher eine Linearkombination:

$\vv{\text{u}} = (1,2,-1) \qquad \vv{\text{v}} = (3,6,-3)$

$\cfrac{3}{1} = \cfrac{6}{2} = \cfrac{-3}{-1} = 3 \ \longrightarrow \ \text{Proporcionales}\ \longrightarrow \ \begin{array}{c} \text{Combinaci\'on}\\[2ex] \text{lineal} \end{array}$

Wenn es schließlich eine lineare Kombination innerhalb einer Menge von Vektoren gibt, bedeutet dies, dass sie linear voneinander abhängig sind, unabhängig davon, ob es sich um einen zweidimensionalen (in R2) oder einen dreidimensionalen (in R3) Vektorraum handelt. Ist hingegen keine Linearkombination zwischen den Vektoren möglich, bedeutet dies, dass sie linear unabhängig sind.

Wenn Ihnen dieses letzte Konzept nicht ganz klar ist, empfehlen wir Ihnen, sich unsere Erklärung zu linear abhängigen und unabhängigen Vektoren anzusehen. Hier finden Sie, was es bedeutet, dass Vektoren linear abhängig oder unabhängig sind, Beispiele für jeden Typ und die Unterschiede zwischen ihnen. . Dieses Konzept wird häufig verwendet und in Prüfungen tatsächlich häufig gefragt, daher ist es wichtig, dass Sie es gut verstehen.

Wie man einen Vektor als lineare Kombination anderer Vektoren ausdrückt

Wir werden dann sehen, wie wir ein typisches Problem lösen können, bei dem wir aufgefordert werden, die Linearkombination eines Vektors zu finden.

Drücken Sie den Vektor aus
$\vv{\text{x}}$

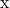
als Linearkombination von

$\vv{\text{u}}, \vv{\text{v}}$

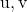
Und

$\vv{\text{w}}.$

$\vv{\text{x}} = (3,1,2)$

$\vv{\text{u}} = (1,0,1) \qquad \vv{\text{v}} = (1,2,0) \qquad \vv{\text{w}} = (0,1,-1)$

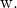
Damit der Vektor

$\vv{\text{x}}$

eine Linearkombination der anderen Vektoren sein, muss die folgende Gleichung erfüllt sein:

$a_1\vv{\text{u}}+a_2\vv{\text{v}}+ a_3\vv{\text{w}}=\vv{\text{x}}$

Wo die Koeffizienten

$a_1, a_2$

Und

$a_3$

Das sind die Unbekannten, die wir finden müssen.

Wir ersetzen daher jeden Vektor durch seine Koordinaten:

$a_1\begin{pmatrix} 1 \\0\\1 \end{pmatrix}+a_2\begin{pmatrix} 1 \\2\\0 \end{pmatrix}+ a_3\begin{pmatrix} 0 \\1\\-1 \end{pmatrix}=\begin{pmatrix} 3 \\1\\2 \end{pmatrix}$

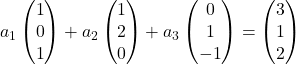
Wir multiplizieren jeden Vektor mit seinem Koeffizienten:

$\begin{pmatrix} a_1 \\0\\a_1 \end{pmatrix}+\begin{pmatrix} a_2 \\2a_2\\0 \end{pmatrix}+ \begin{pmatrix} 0 \\a_3\\-a_3 \end{pmatrix}=\begin{pmatrix} 3 \\1\\2 \end{pmatrix}$

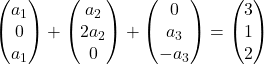
Wir fügen Vektoren hinzu:

$\begin{pmatrix} a_1 +a_2\\2a_2+a_3\\a_1-a_3 \end{pmatrix}=\begin{pmatrix} 3 \\1\\2 \end{pmatrix}$

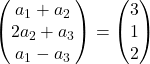
Jede linke Koordinate muss gleich jeder rechten Koordinate sein. Wir haben daher 3 Gleichungen:

$\left. \begin{array}{l} a_1 +a_2 = 3 \\[2ex] 2a_2+a_3 =1\\[2ex] a_1-a_3 = 2 \end{array} \right\}$

Es bleibt nur noch die Lösung des erhaltenen Gleichungssystems. Verwenden Sie dazu die von Ihnen bevorzugte Methode (Substitutionsmethode, Cramer-Regel, Gauß-Jordan-Methode usw.). In diesem Fall verwenden wir die Gauß-Methode:

$\left( \begin{array}{ccc|c} 1&1&0& 3 \\[2ex] 0&2&1&1\\[2ex] 1&0&-1&2 \end{array} \right)$

$\left(\begin{array}{ccc|c} 1&1&0& 3 \\[2ex] 0&2&1&1\\[2ex] 1&0&-1&2 \end{array} \right) \begin{array}{c} \\[2ex] \\[2ex] \xrightarrow{F_3-F_1} \end{array} \left( \begin{array}{ccc|c} 1&1&0& 3 \\[2ex] 0&2&1&1\\[2ex] 0&-1&-1&-1 \end{array} \right)$

$\left( \begin{array}{ccc|c} 1&1&0& 3 \\[2ex] 0&2&1&1\\[2ex] 0&-1&-1&-1 \end{array} \right)\begin{array}{c} \\[2ex] \\[2ex] \xrightarrow{2F_3+F_2}\end{array} \left( \begin{array}{ccc|c} 1&1&0& 3 \\[2ex] 0&2&1&1\\[2ex] 0&0&-1&-1 \end{array}\right)$

Das erhaltene Schrittsystem lautet daher:

$\left. \begin{array}{r} a_1 +a_2 = 3 \\[2ex] 2a_2+a_3 =1\\[2ex] -a_3 = -1 \end{array} \right\}$

Jetzt müssen wir nur noch das Unbekannte klären und seinen Wert herausfinden. Aus der letzten Gleichung finden wir also

$a_3:$

$-a_3 = -1 \ \longrightarrow \ \bm{a_3 = 1}$

Aus der zweiten Gleichung des Systems berechnen wir den Wert von

$a_2:$

$2a_2+a_3 =1 \ \xrightarrow{a_3\ = \ 1} \ 2a_2+1=1$

$2a_2=1-1$

$2a_2=0$

$\bm{a_2=0}$

Und schließlich finden wir aus der ersten Gleichung des Stufensystems die Unbekannte

$a_1:$

$a_1 +a_2 = 3 \ \xrightarrow{a_3\ = \ 1 \ ; \ a_2 \ = \ 0 } \ \bm{a_1 = 3}$

Die Lösung des linearen Gleichungssystems lautet daher:

$a_1=3 \qquad a_2=0 \qquad a_3 = 1$

Also der Vektor

$\vv{\text{x}}$

Es kann durch die folgende Linearkombination ausgedrückt werden:

$\vv{\text{x}}= a_1\vv{\text{u}}+a_2\vv{\text{v}}+ a_3\vv{\text{w}}$

$\vv{\text{x}}= 3\vv{\text{u}}+0\vv{\text{v}}+ 1\vv{\text{w}}$

$\vv{\mathbf{x}}\bm{= 3}\vv{\mathbf{u}} \bm{+} \vv{\mathbf{w}}}$

Es besteht also faktisch eine lineare Abhängigkeit zwischen den Vektoren. Wenn andererseits keine Lösung des Gleichungssystems gefunden worden wäre, würde dies bedeuten, dass der Vektor

$\vv{\text{x}}$

Er ist linear unabhängig von den anderen Vektoren und daher wäre keine lineare Kombination möglich, um diesen Vektor aus den anderen Vektoren zu erhalten.

Aufgaben zur Linearkombination von Vektoren gelöst

Übung 1

Geben Sie unter den folgenden drei Vektoren an, welche Paare lineare Kombinationen voneinander sind. Ermitteln Sie außerdem die lineare Kombinationsbeziehung dieser Vektorpaare.

$\vv{\text{u}} = (2,4,3) \qquad \vv{\text{v}} = (1,2,-3) \qquad \vv{\text{w}} = (-3,-6,9)$

Sehen Sie sich die Lösung an

Um zu wissen, ob ein Vektorpaar eine Linearkombination ist, müssen wir prüfen, ob ihre Koordinaten proportional sind.

Wir prüfen zunächst den Vektor

$\vv{\text{u}}$

mit dem Vektor

$\vv{\text{v}} :$

$\cfrac{2}{1} = \cfrac{4}{2} \neq \cfrac{3}{-3} \ \longrightarrow \ \text{No proporcionales}$

Zweitens überprüfen wir den Vektor

$\vv{\text{u}}$

mit dem Vektor

$\vv{\text{w}} :$

$\cfrac{2}{-3} = \cfrac{4}{-6} \neq \cfrac{3}{9} \ \longrightarrow \ \text{No proporcionales}$

Abschließend testen wir den Vektor

$\vv{\text{v}}$

mit dem Vektor

$\vv{\text{w}} :$

$\cfrac{1}{-3} = \cfrac{2}{-6} = \cfrac{-3}{9} = -\cfrac{1}{3} \ \longrightarrow \ \text{Proporcionales}\ \longrightarrow \ \begin{array}{c} \text{Combinaci\'on}\\[2ex] \text{lineal} \end{array}$

Das einzige Vektorpaar, das eine Linearkombination ist, ist also

$\vv{\text{v}}$

Und

$\vv{\text{w}}.$

Darüber hinaus ist ihre Beziehung wie folgt:

$\vv{\text{v}}= -\cfrac{1}{3} \vv{\text{w}}$

Oder gleichwertig:

$\vv{\text{w}}= -3 \vv{\text{v}}$

Obwohl die Anweisung dies nicht erfordert, sind es die einzigen Vektoren, die linear voneinander abhängen

$\vv{\text{v}}$

Und

$\vv{\text{w}}$

weil es eine lineare Kombination zwischen ihnen gibt. Die anderen Paare sind linear unabhängig, da sie nicht linear kombiniert werden können.

Übung 2

Finden Sie die lineare Beziehung zwischen dem Vektor

$\vv{\text{x}}$

und die Menge der Vektoren

$\vv{\text{u}}, \vv{\text{v}}$

Und

$\vv{\text{w}}.$

$\vv{\text{x}} = (4,2,5)$

$\vv{\text{u}} = (1,-1,0) \qquad \vv{\text{v}} = (1,2,2) \qquad \vv{\text{w}} = (-1,1,-1)$

Sehen Sie sich die Lösung an

Damit der Vektor

$\vv{\text{x}}$

eine Linearkombination der anderen Vektoren sein, muss die folgende Gleichung erfüllt sein:

$a_1\vv{\text{u}}+a_2\vv{\text{v}}+ a_3\vv{\text{w}}=\vv{\text{x}}$

Wir ersetzen daher jeden Vektor durch seine Koordinaten:

$a_1\begin{pmatrix} 1 \\-1\\0 \end{pmatrix}+a_2\begin{pmatrix} 1 \\2\\2 \end{pmatrix}+ a_3\begin{pmatrix} -1 \\1\\-1 \end{pmatrix}=\begin{pmatrix} 4 \\2\\5 \end{pmatrix}$

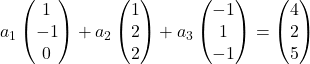
Wir multiplizieren jeden Vektor mit seiner Konstante:

$\begin{pmatrix} a_1 \\-a_1\\0 \end{pmatrix}+\begin{pmatrix} a_2 \\2a_2\\2a_2 \end{pmatrix}+ \begin{pmatrix} -a_3 \\a_3\\-a_3 \end{pmatrix}=\begin{pmatrix} 4 \\2\\5 \end{pmatrix}$

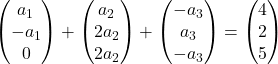
Wir addieren die Vektoren:

$\begin{pmatrix} a_1 +a_2-a_3\\-a_1+2a_2+a_3\\ 2a_2-a_3 \end{pmatrix}=\begin{pmatrix} 4 \\2\\5 \end{pmatrix}$

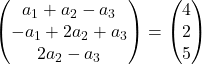
Wir erhalten daher das folgende Gleichungssystem:

$\left. \begin{array}{l} a_1 +a_2-a_3 = 4 \\[2ex] -a_1+2a_2+a_3 =2\\[2ex] 2a_2-a_3 = 5 \end{array} \right\}$

Wir lösen das mit der Gauß-Methode erhaltene System:

$\left( \begin{array}{ccc|c} 1&1&-1& 4 \\[2ex] -1&2&1&2\\[2ex] 0&2&-1&5 \end{array} \right)$

$\left(\begin{array}{ccc|c} 1&1&-1& 4 \\[2ex] -1&2&1&2\\[2ex] 0&2&-1&5 \end{array} \right) \begin{array}{c} \\[2ex] \xrightarrow{F_2+F_1}\\[2ex] & \end{array} \left( \begin{array}{ccc|c} 1&1&-1& 4 \\[2ex] 0&3&0&6\\[2ex] 0&2&-1&5\end{array} \right)$

$\left(\begin{array}{ccc|c} 1&1&-1& 4 \\[2ex] 0&3&0&6\\[2ex] 0&2&-1&5 \end{array} \right) \begin{array}{c} \\[2ex] \\[2ex] \xrightarrow{3F_3-2F_2} \end{array} \left( \begin{array}{ccc|c} 1&1&-1& 4 \\[2ex] 0&3&0&6\\[2ex] 0&0&-3&3\end{array} \right)$

Das erhaltene Schrittsystem lautet daher:

$\left. \begin{array}{r} a_1 +a_2-a_3 = 4 \\[2ex] 3a_2 =6\\[2ex] -3a_3 = 3 \end{array} \right\}$

Jetzt müssen wir nur noch das Unbekannte klären und seinen Wert herausfinden. Aus der letzten Gleichung finden wir also

$a_3:$

$-3a_3 = 3$

$a_3 = \cfrac{3}{-3} = -1$

Aus der zweiten Gleichung des Systems berechnen wir den Wert von

$a_2:$

$3a_2=6$

$a_2=\cfrac{6}{3} = 2$

Und schließlich finden wir aus der ersten Gleichung des Stufensystems die Unbekannte

$a_1:$

$a_1 +a_2-a_3 = 4 \ \xrightarrow{a_3\ = \ -1 \ ; \ a_2 \ = \ 2 } \ a_1 +2-(-1) = 4$

$a_1 = 4-2-1$

$a_1 = 1$

Die Lösung des linearen Gleichungssystems lautet daher:

$a_1=1 \qquad a_2=2 \qquad a_3 = -1$

Also der Vektor

$\vv{\text{x}}$

Es kann durch die folgende Linearkombination ausgedrückt werden:

$\vv{\text{x}}= a_1\vv{\text{u}}+a_2\vv{\text{v}}+ a_3\vv{\text{w}}$

$\vv{\text{x}}= 1\vv{\text{u}}+2\vv{\text{v}}-1\vv{\text{w}}$

$\vv{\mathbf{x}}\bm{= }\vv{\mathbf{u}}\bm{+} \bm{2} \vv{\mathbf{v}} \bm{-} \vv{\mathbf{w}}$

Übung 3

Drücken Sie den Vektor aus

$\vv{\text{x}}$

als Linearkombination von Vektoren

$\vv{\text{u}}, \vv{\text{v}}$

Und

$\vv{\text{w}}.$

$\vv{\text{x}} = (-1,5,-3)$

$\vv{\text{u}} = (1,3,-1) \qquad \vv{\text{v}} = (2,-3,-2) \qquad \vv{\text{w}} = (0,-2,1)$

Sehen Sie sich die Lösung an

Wir schlagen die lineare Kombinationsgleichung bezüglich des Vektors vor

$\vv{\text{x}} :$

$a_1\vv{\text{u}}+a_2\vv{\text{v}}+ a_3\vv{\text{w}}=\vv{\text{x}}$

Wir ersetzen daher jeden Vektor durch seine Komponenten:

$a_1\begin{pmatrix} 1 \\3\\-1 \end{pmatrix}+a_2\begin{pmatrix} 2 \\-3\\-2 \end{pmatrix}+ a_3\begin{pmatrix} 0 \\-2\\1 \end{pmatrix}=\begin{pmatrix} -1 \\5\\-3 \end{pmatrix}$

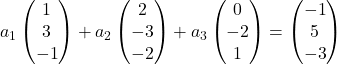
Wir multiplizieren jeden Vektor mit seiner jeweiligen Unbekannten:

$\begin{pmatrix} a_1 \\3a_1\\-a_1 \end{pmatrix}+\begin{pmatrix} 2a_2 \\ -3a_2\\ -2a_2 \end{pmatrix}+ \begin{pmatrix} 0 \\-2a_3\\a_3 \end{pmatrix}=\begin{pmatrix} -1 \\5\\-3 \end{pmatrix}$

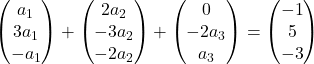
Wir führen die Addition von Vektoren durch:

$\begin{pmatrix} a_1 +2a_2\\3a_1-3a_2-2a_3\\ -a_1-2a_2+a_3 \end{pmatrix}=\begin{pmatrix} -1 \\5\\-3 \end{pmatrix}$

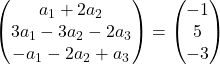
Wir haben daher das folgende Gleichungssystem erhalten:

$\left. \begin{array}{l} a_1 +2a_2 = -1 \\[2ex] 3a_1-3a_2-2a_3 =5\\[2ex] -a_1-2a_2+a_3 = -3 \end{array} \right\}$

Wir lösen das mit der Gauß-Methode erhaltene System:

$\left( \begin{array}{ccc|c} 1&2&0& -1 \\[2ex] 3&-3&-2&5\\[2ex] -1&-2&1&-3 \end{array} \right)$

$\left(\begin{array}{ccc|c} 1&2&0& -1 \\[2ex] 3&-3&-2&5\\[2ex] -1&-2&1&-3 \end{array} \right) \begin{array}{c} \\[2ex] \xrightarrow{F_2-3F_1}\\[2ex] \xrightarrow{F_3+F_1} \end{array} \left( \begin{array}{ccc|c} 1&2&0& -1 \\[2ex] 0&-9&-2&8\\[2ex] 0&0&1&-4\end{array} \right)$

Das erhaltene Schrittsystem lautet daher:

$\left. \begin{array}{r} a_1 +2a_2 = -1 \\[2ex] -9a_2-2a_3 =8\\[2ex] a_3 = -4 \end{array} \right\}$

Jetzt müssen wir nur noch das Unbekannte klären und seinen Wert herausfinden. Aus der letzten Gleichung finden wir also

$a_3:$

$a_3 = -4$

Aus der zweiten Gleichung des Systems ermitteln wir den Wert von

$a_2:$

$-9a_2-2a_3 =8 \ \xrightarrow{a_3 \ = \ -4} \ -9a_2-2\cdot (-4) = 8$

$-9a_2+8 = 8$

$-9a_2 = 8-8$

$-9a_2 = 0$

$a_2=\cfrac{0}{-9} = 0$

Und schließlich lösen wir aus der ersten Gleichung des Stufensystems die Unbekannte

$a_1:$

$a_1 +2a_2 = -1 \ \xrightarrow{a_2 \ = \ 0 } \ a_1=-1$

Die Lösung des linearen Gleichungssystems lautet daher:

$a_1=-1 \qquad a_2=0 \qquad a_3 = -4$

Also der Vektor

$\vv{\text{x}}$

kann durch lineare Kombination der anderen Vektoren ausgedrückt werden:

$\vv{\text{x}}= a_1\vv{\text{u}}+a_2\vv{\text{v}}+ a_3\vv{\text{w}}$

$\vv{\text{x}}= -1\vv{\text{u}}+0\vv{\text{v}}-4\vv{\text{w}}$

$\vv{\mathbf{x}}\bm{= -}\vv{\mathbf{u}}\bm{-4} \vv{\mathbf{w}}$

Übung 4

Bestimmen Sie, ob der Vektor

$\vv{\text{x}}$

kann als Linearkombination aus den Vektoren ausgedrückt werden

$\vv{\text{u}}, \vv{\text{v}}$

Und

$\vv{\text{w}}.$

Finden Sie in diesem Fall den Ausdruck, der sie verbindet.

$\vv{\text{x}} = (2,1,-1)$

$\vv{\text{u}} = (3,-1,1) \qquad \vv{\text{v}} = (-1,2,0) \qquad \vv{\text{w}} = (1,3,1)$

Sehen Sie sich die Lösung an

Damit der Vektor

$\vv{\text{x}}$

eine Linearkombination der anderen Vektoren sein, muss die folgende Gleichung erfüllt sein:

$a_1\vv{\text{u}}+a_2\vv{\text{v}}+ a_3\vv{\text{w}}=\vv{\text{x}}$

Wir ersetzen daher jeden Vektor durch seine Koordinaten:

$a_1\begin{pmatrix} 3 \\-1\\1 \end{pmatrix}+a_2\begin{pmatrix} -1 \\2\\0 \end{pmatrix}+ a_3\begin{pmatrix} 1 \\3\\1 \end{pmatrix}=\begin{pmatrix} 2 \\1\\-1 \end{pmatrix}$

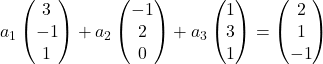
Wir multiplizieren jeden Vektor mit seinem Koeffizienten:

$\begin{pmatrix} 3a_1 \\-a_1\\a_1 \end{pmatrix}+\begin{pmatrix} -a_2 \\2a_2\\0 \end{pmatrix}+ \begin{pmatrix} a_3 \\3a_3\\a_3 \end{pmatrix}=\begin{pmatrix} 2 \\1\\-1 \end{pmatrix}$

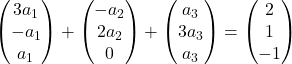
Wir addieren die Vektoren:

$\begin{pmatrix} 3a_1 -a_2+a_3\\-a_1+2a_2+3a_3\\ a_1+a_3 \end{pmatrix}=\begin{pmatrix} 2 \\1\\-1 \end{pmatrix}$

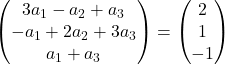
Der vorherige Ausdruck entspricht daher dem folgenden Gleichungssystem:

$\left. \begin{array}{l} 3a_1 -a_2+a_3 = 2 \\[2ex] -a_1+2a_2+3a_3 =1\\[2ex] a_1+a_3 = -1 \end{array} \right\}$

Wir lösen nun das mit der Gauß-Methode erhaltene System:

$\left( \begin{array}{ccc|c} 3&-1&1& 2 \\[2ex] -1&2&3&1\\[2ex] 1&0&1&-1 \end{array} \right)$

$\left(\begin{array}{ccc|c} 3&-1&1& 2 \\[2ex] -1&2&3&1\\[2ex] 1&0&1&-1 \end{array} \right) \begin{array}{c} \\[2ex] \xrightarrow{3F_2+F_1}\\[2ex] \xrightarrow{3F_3-F_1} \end{array} \left( \begin{array}{ccc|c} 3&-1&1& 2 \\[2ex] 0&5&10&5\\[2ex] 0&1&2&-5\end{array} \right)$

$\left(\begin{array}{ccc|c} 3&-1&1& 2 \\[2ex] 0&5&10&5\\[2ex] 0&1&2&-5 \end{array} \right) \begin{array}{c} \\[2ex] \\[2ex] \xrightarrow{5F_3-F_2} \end{array} \left( \begin{array}{ccc|c}3&-1&1& 2 \\[2ex] 0&5&10&5\\[2ex] 0&0&0&-30\end{array} \right)$

Wir haben daher das folgende Gleichungssystem erhalten:

$\left. \begin{array}{r} 3a_1 -a_2+a_3 = 2 \\[2ex] 5a_2 +10a_3=5\\[2ex] 0 = -30 \end{array} \right\}$

Die letzte Gleichung kann jedoch niemals erfüllt werden, da 0 niemals gleich -30 sein wird, egal welche Werte die Unbekannten annehmen. Daher hat das System keine Lösung und dies impliziert, dass es keine Linearkombination zur Berechnung des Vektors gibt

$\vv{\text{x}}.$

Linearkombination von vektoren

Was ist eine Linearkombination von Vektoren?

Wie man einen Vektor als lineare Kombination anderer Vektoren ausdrückt

Aufgaben zur Linearkombination von Vektoren gelöst

Übung 1

Übung 2

Übung 3

Übung 4

Kommentar verfassen Kommentieren abbrechen