Auf dieser Seite erklären wir, wie man die Polynomzerlegung (oder den Ausdruck) einer Zahl durchführt. Hier sehen Sie Beispiele für Polynomzerlegungen und finden darüber hinaus gelöste Schritt-für-Schritt-Übungen zum Üben.
Was ist die Polynomzerlegung einer Zahl?
In der Mathematik besteht die Polynomzerlegung einer Zahl darin, diese Zahl in einer Summe auszudrücken, sodass jeder Term der Summe ein Produkt jeder Ziffer der Zahl mit einer Potenz zur Basis 10 ist.
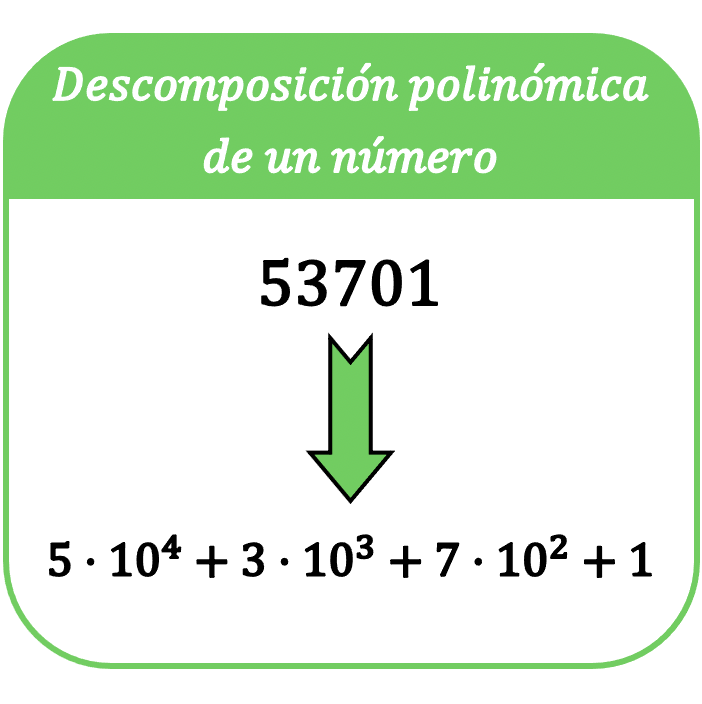
Der Begriff polynomiale Zerlegung einer Zahl wird auch als polynomialer Ausdruck einer Zahl bezeichnet.
So führen Sie eine Polynomzerlegung durch
Um eine Polynomzerlegung einer Zahl durchzuführen, müssen Sie jede Ziffer der Zahl mit 10 multiplizieren, um die Anzahl der Ziffern auf der rechten Seite zu erhöhen .
Wenn wir beispielsweise die Polynomzerlegung der folgenden Zahl berechnen möchten:
![]()
In diesem Fall steht die Zahl 8 an fünfter Stelle, hat also 4 Ziffern rechts davon. Wir müssen also acht mit zehn hoch vier multiplizieren:
![]()
Um also die Zahl 86293 polynomial zu zerlegen, müssen Sie dasselbe mit allen Ziffern der Zahl machen und alle Multiplikationen in Form einer Summe ausdrücken:
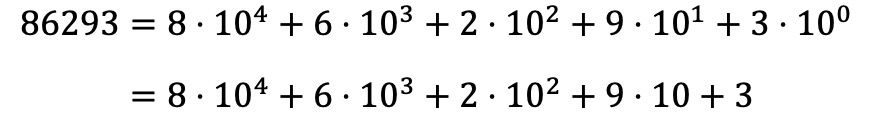
Beachten Sie, dass die Potenz 10 0 verschwindet, da gemäß den Potenzeigenschaften jede auf 0 erhöhte Zahl gleich 1 ist, also 10 0 =1.
Andererseits kann man die polynomiale Zerlegung einer Zahl auch aus ihrer multiplikativen Zerlegung ermitteln:
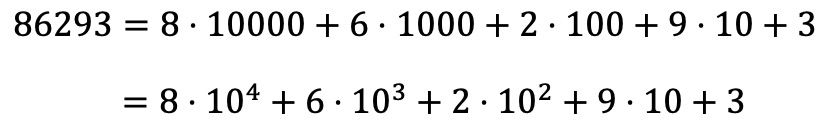
Beispiele für Polynomzerlegungen von Zahlen
Nachdem wir gesehen haben, wie die Polynomzerlegung einer Zahl durchgeführt wird, werden wir uns verschiedene Beispiele dieser Art von Operation ansehen, um das Konzept vollständig zu verstehen.
- Polynomzerlegung von 3641:
![]()
- Polynomzerlegung von 56912:
![]()
- Polynomzerlegung von 27084:
![Rendered by QuickLaTeX.com \begin{aligned} 27084 &= 2\cdot 10^4 +7\cdot 10^3 +0\cdot 10^2 + 8\cdot 10 + 4 \\[2ex] & = 2\cdot 10^4 +7\cdot 10^3 + 8\cdot 10 + 4 \end{aligned}](https://mathority.org/wp-content/ql-cache/quicklatex.com-f72230330ff9c9150dc9ab19a89a42d8_l3.png)
In diesem letzten Beispiel können wir die dritte Multiplikation vereinfachen, da sich jede mit Null multiplizierte Zahl aufhebt.
Polynomzerlegung von Dezimalzahlen
Wir haben gerade gesehen, wie man die Polynomzerlegung der natürlichen Zahlen durchführt. Aber … wie zerlegt man eine Dezimalzahl polynomisch?
Nun, die Polynomzerlegung mit Dezimalzahlen erfolgt auf die gleiche Weise wie mit ganzen Zahlen, aber zusätzlich addieren wir das Produkt jeder Dezimalziffer multipliziert mit einer Potenz zur Basis 10, deren Exponent die Dezimalstelle ist, die die Zahl mit einem negativen Wert einnimmt Zeichen.
Mit Worten erklärt kann dies sehr kompliziert erscheinen, aber Sie werden sehen, dass es anhand eines Beispiels besser verständlich ist:
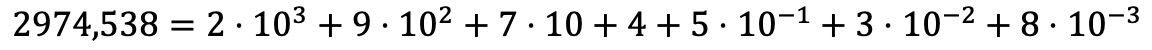
Übungen zur Polynomzerlegung gelöst
Damit Sie Polynomzerlegungen üben können, haben wir mehrere Übungen vorbereitet, die Schritt für Schritt gelöst werden.
Vergessen Sie nicht, dass Sie uns in den Kommentaren alle Fragen stellen können, die Sie haben! 🤔🤔🤔
Übung 1
Führen Sie die Polynomzerlegung der folgenden Zahlen durch:
![]()
![]()
![]()
![]()
Um die Polynomzerlegung einer beliebigen Zahl zu ermitteln, multiplizieren Sie jede Ziffer dieser Zahl mit 10 mit der Anzahl der Ziffern rechts und addieren Sie dann alle Multiplikationen. Noch:
![]()
![]()
![]()
![]()
Übung 2
Finden Sie die Polynomzerlegung der folgenden Zahlen:
![]()
![]()
![]()
![]()
Um eine Zahl polynomiell zu zerlegen, müssen Sie jede Ziffer dieser Zahl mit zehn mit der Anzahl der Ziffern rechts davon multiplizieren und dann alle Produkte addieren. Noch:
![]()
![Rendered by QuickLaTeX.com \text{B)} \ \begin{aligned} 3030 & = 3 \cdot 10^3+ 0\cdot 10^2 +3 \cdot 10 +0 \\[2ex] &= 3 \cdot 10^3+3 \cdot 10 \end{aligned}](https://mathority.org/wp-content/ql-cache/quicklatex.com-0e3500d6a94685566b267e8708e8b0d7_l3.png)
![]()
![]()
Übung 3
Berechnen Sie die Polynomzerlegung der folgenden Dezimalzahlen:
![]()
![]()
![]()
![]()
In diesem Problem sind alle Zahlen dezimal. Um sie zu zerlegen, müssen Sie also jede nichtdezimale Ziffer mit 10 multiplizieren, erhöht auf die Anzahl der Ziffern, die sie bis zum Dezimalpunkt hat, und jede Dezimalziffer mit 10 multiplizieren, die auf ihre Dezimalstelle erhöht ist ein negatives Vorzeichen.
![]()
![]()
![Rendered by QuickLaTeX.com \text{C)} \ \begin{aligned} 0,82694 & = 0 + 8 \cdot 10^{-1} +2 \cdot 10^{-2}+6\cdot 10^{-3}+9\cdot 10^{-4} +4\cdot 10^{-5}\\[2ex] & = 8 \cdot 10^{-1} +2 \cdot 10^{-2}+6\cdot 10^{-3}+9\cdot 10^{-4} +4\cdot 10^{-5}\end{aligned}](https://mathority.org/wp-content/ql-cache/quicklatex.com-deb6b85265df2e98bcb5e116e19c397f_l3.png)
![Rendered by QuickLaTeX.com \text{D)} \ \begin{aligned} 5,7201 & = 5 + 7 \cdot 10^{-1} +2 \cdot 10^{-2}+0\cdot 10^{-3}+1\cdot 10^{-4}\\[2ex] & = 5 + 7 \cdot 10^{-1} +2 \cdot 10^{-2}+1\cdot 10^{-4} \end{aligned}](https://mathority.org/wp-content/ql-cache/quicklatex.com-8e204c24ba4f9138f503cf2c2a0e379d_l3.png)