Algebraische Brüche: Vereinfachung, Operationen, gelöste Aufgaben usw. -

Auf dieser Seite erklären wir, was algebraische Brüche sind, wann sie äquivalent sind, wie man sie vereinfacht und wie man Operationen mit algebraischen Brüchen durchführt (Addition, Subtraktion, Multiplikation und Division). Darüber hinaus können Sie gelöste Schritt-für-Schritt-Übungen für algebraische Brüche sehen. Kurz gesagt, hier finden Sie alles über algebraische Brüche.

Was sind algebraische Brüche?

In der Mathematik ist ein algebraischer Bruch ein Bruch, der ein Polynom im Zähler und ein weiteres Polynom im Nenner hat.

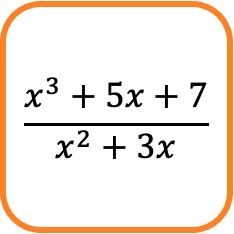
Der obige Bruchausdruck besteht beispielsweise aus einem algebraischen Bruch, da Zähler und Nenner aus Polynomen bestehen.

Algebraisches Bruchäquivalent

Sobald wir die Definition algebraischer Brüche kennen, wollen wir sehen, wann zwei solcher Brüche gleich sind.

Mathematisch sind zwei algebraische Brüche äquivalent , wenn die folgende Bedingung erfüllt ist:

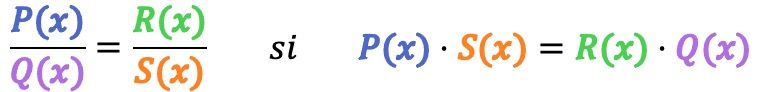
Als Beispiel prüfen wir, ob die folgenden zwei algebraischen Brüche äquivalent sind:

$\cfrac{x+3}{x^2+5x+6} \qquad \cfrac{1}{x+2}$

Um festzustellen, ob Brüche algebraisch gleich sind, multiplizieren wir ihre Terme transversal:

$(x+3)\cdot (x+2) = (x^2+5x+6)\cdot 1$

Berechnen wir nun die Multiplikationen von Polynomen:

$x^2+2x+3x+6 = x^2+5x+6$

$x^2+5x+6 = x^2+5x+6$

Wir haben auf beiden Seiten der Gleichung den gleichen Ausdruck, es handelt sich also praktisch um zwei äquivalente algebraische Brüche.

Vereinfachen Sie algebraische Brüche

Um einen algebraischen Bruch zu vereinfachen, müssen Sie zunächst die Polynome im Zähler und Nenner faktorisieren und dann die gemeinsamen Faktoren eliminieren.

Um algebraische Brüche zu vereinfachen, ist es natürlich wichtig, dass Sie wissen , was Polynomfaktorisierung ist und wie sie durchgeführt wird. Wenn Sie immer noch nicht wissen, wie Polynome faktorisiert werden, oder sich nicht vollständig daran erinnern können, empfehle ich Ihnen, die verlinkte Seite aufzurufen, bevor Sie fortfahren, sonst werden Sie die Vorgehensweise kaum verstehen. Es erklärt Schritt für Schritt, wie man Polynome faktorisiert, außerdem können Sie sich mehrere Beispiele ansehen und anhand gelöster Aufgaben üben.

Sehen wir uns nun anhand eines Beispiels an, wie ein algebraischer Bruch vereinfacht wird, indem die Methode der Faktorisierung von Polynomen angewendet wird:

Vereinfachen Sie den folgenden algebraischen Bruch:

$\cfrac{x^3+2x^2-x-2}{x^2-2x+1}$

Zuerst faktorisieren wir die Polynome des Zählers und Nenners des Bruchs:

$\cfrac{(x-1)(x+1)(x+2)}{(x-1)(x-1)}$

⬆(Wenn Sie nicht wissen, wie Polynome faktorisiert wurden, schauen Sie sich den Link oben an)⬆

Und sobald wir die Polynome faktorisiert haben, eliminieren wir die gemeinsamen Faktoren zwischen Zähler und Nenner, das heißt, wir entfernen alle Terme, die sich wiederholen:

$\cfrac{\cancel{(x-1)}(x+1)(x+2)}{\cancel{(x-1)}(x-1)}$

Der vereinfachte algebraische Bruch sieht daher wie folgt aus:

$\cfrac{(x+1)(x+2)}{x-1}$

In dieser Aufgabe wurden die Polynome des algebraischen Bruchs durch Finden ihrer Wurzeln faktorisiert; Manchmal kann ein Polynom jedoch direkt faktorisiert werden, indem der gemeinsame Faktor verwendet wird (viel schnellere Methode). In diesem Link erfahren Sie, was es bedeutet, aus einem Polynom einen gemeinsamen Faktor zu ziehen , und Sie erfahren , wie Sie einen algebraischen Bruch mithilfe eines gemeinsamen Faktors vereinfachen können .

Operationen mit algebraischen Brüchen

Wie jede Art von Brüchen können auch Operationen mit algebraischen Brüchen durchgeführt werden. Insbesondere können algebraische Brüche addiert, subtrahiert, multipliziert und dividiert werden. Im Folgenden erklären wir Schritt für Schritt anhand von Beispielen, wie die einzelnen Operationsarten berechnet werden.

Algebraische Brüche addieren und subtrahieren

Das Verfahren zum Addieren und Subtrahieren algebraischer Brüche ist praktisch identisch, daher werden wir sie gemeinsam analysieren. Zuerst sehen wir ein Beispiel für die Addition zweier algebraischer Brüche und im Folgenden untersuchen wir den Unterschied zwischen der Methode zum Subtrahieren algebraischer Brüche.

Algebraische Brüche addieren

Das Addieren algebraischer Brüche erfolgt auf die gleiche Weise wie bei normalen Brüchen: Reduzieren Sie zuerst die Brüche auf einen gemeinsamen Nenner und addieren Sie dann die Zähler.

Sehen wir uns anhand eines Beispiels an, wie algebraische Brüche addiert werden:

$\cfrac{x}{x^2+2x+1} + \cfrac{3x}{x^2+x}$

Wir faktorisieren zunächst die Nenner der Brüche:

$\cfrac{x}{(x+1)(x+1)} + \cfrac{3x}{x(x+1)}$

$\cfrac{x}{(x+1)^2} + \cfrac{3x}{x(x+1)}$

Wir müssen nun das lcm (kleinstes gemeinsames Vielfaches) der Nenner ermitteln, um die Brüche auf einen gemeinsamen Nenner zu reduzieren.

Tipp: Der lcm der Nenner wird immer aus dem Produkt der ihnen gemeinsamen Faktoren, erhöht zum größten Exponenten, multipliziert mit den nicht-gemeinsamen Faktoren gebildet.

Zum Beispiel in unserem Fall

$\cfrac{x}{(x+1)^2} + \cfrac{3x}{x(x+1)}$

Der gemeinsame Teiler zwischen den zum größten Exponenten erhobenen Nennern ist

$(x+1)^2.$

Und der nicht gemeinsame Faktor zwischen den Nennern ist

$x.$

Daher beträgt der lcm der Nenner in diesem Fall:

$(x+1)^2 \cdot x$

Der lcm der Nenner beträgt daher

$(x+1)^2 \cdot x,$

Dies wird daher der neue Nenner der beiden Brüche sein.

$\cfrac{x}{(x+1)^2} + \cfrac{3x}{x(x+1)} \ \longrightarrow \ \cfrac{}{x(x+1)^2} + \cfrac{}{x(x+1)^2}$

Sobald wir den gemeinsamen Nenner gefunden haben, müssen wir die Zähler ändern. Dazu gehen wir genauso vor wie bei der Addition normaler Brüche: Für jeden Bruch dividieren wir den lcm

$\bigl( \ x(x+1)^2 \ \bigr)$

zwischen dem ursprünglichen Nenner und multiplizieren Sie das Ergebnis mit dem Zähler:

$\cfrac{x(x+1)^2}{(x+1)^2} = \cfrac{x\cancel{(x+1)^2}}{\cancel{(x+1)^2}} = \color{red}\bm{x}$

$\cfrac{x(x+1)^2}{x(x+1)}= \cfrac{\cancel{x}(x+1)^\cancel{2}}{\cancel{x}\cancel{(x+1)}}=\color{blue} \bm{x+1}$

$\cfrac{x}{(x+1)^2} + \cfrac{3x}{x(x+1)} \ \longrightarrow \ \cfrac{x \cdot \color{red}\bm{x} \color{black} }{x(x+1)^2} + \cfrac{3x \cdot \color{blue} \bm{(x+1)} \color{black}}{x(x+1)^2}$

Jetzt können wir die beiden Brüche zusammenzählen, weil sie den gleichen Nenner haben:

$\cfrac{x^2+3x(x+1)}{x(x+1)^2}$

Schließlich operieren wir mit dem Zähler. Wir bilden zunächst das Produkt aus Monom und Polynom:

$\cfrac{x^2 +3x\cdot x+ 3x\cdot 1 }{x(x+1)^2}$

$\cfrac{x^2 +3x^2 + 3x }{x(x+1)^2}$

Als nächstes fügen wir die ähnlichen Terme zum Zähler hinzu:

$\cfrac{4x^2 + 3x }{x(x+1)^2}$

Normalerweise wären wir schon da, aber wenn wir uns dieses Problem genauer ansehen, können wir den algebraischen Bruch noch weiter vereinfachen, indem wir einen gemeinsamen Faktor aus dem Zähler entfernen. Noch:

$\cfrac{x(4x + 3)}{x(x+1)^2}$

$\cfrac{\cancel{x}(4x + 3)}{\cancel{x}(x+1)^2}$

$\cfrac{4x + 3}{(x+1)^2}$

Damit haben wir die Summe der beiden algebraischen Brüche bereits vervollständigt.

Subtraktion algebraischer Brüche

Um algebraische Brüche zu subtrahieren, müssen wir einem ähnlichen Verfahren wie beim Addieren algebraischer Brüche folgen: Zuerst die Brüche auf einen gemeinsamen Nenner reduzieren und dann die Zähler subtrahieren.

Sehen wir uns anhand eines Beispiels an, wie algebraische Brüche subtrahiert werden:

$\cfrac{2x}{x^2-x-6} - \cfrac{4x-3}{(x+2)^2}$

Zuerst müssen wir die Nenner der beiden Brüche faktorisieren:

$\cfrac{2x}{(x+2)(x-3)} - \cfrac{4x-3}{(x+2)^2}$

Wie bei der Subtraktion normaler Brüche müssen wir nun das lcm (kleinstes gemeinsames Vielfaches) der Nenner berechnen, um die Brüche auf einen gemeinsamen Nenner zu reduzieren. In diesem Fall beträgt der lcm der Nenner

$(x+2)^2(x-3) ,$

Dies wird daher der neue Nenner der beiden Brüche sein.

$\cfrac{2x}{(x+2)(x-3)} - \cfrac{4x-3}{(x+2)^2} \ \longrightarrow \ \cfrac{}{(x+2)^2(x-3)} + \cfrac{}{(x+2)^2(x-3)}$

Jetzt wenden wir das gleiche Verfahren wie beim Subtrahieren normaler Brüche an: Für jeden Bruch dividieren wir den lcm

$\bigl( \ x(x+1)^2 \ \bigr)$

zwischen dem ursprünglichen Nenner und multiplizieren Sie das Ergebnis mit dem Zähler:

$\cfrac{(x+2)^2(x-3)}{(x+2)(x-3)} = \cfrac{(x+2)^{\cancel{2}}\cancel{(x-3)}}{\canel{(x+2)}\cancel{(x-3)}} = \color{red}\bm{x+2}$

$\cfrac{(x+2)^2(x-3)}{(x+2)^2}= \cfrac{\cancel{(x+2)^2}(x-3)}{\cancel{(x+2)^2}}=\color{blue} \bm{x-3}$

$\cfrac{2x}{(x+2)(x-3)} - \cfrac{4x-3}{(x+2)^2} \ \longrightarrow \ \cfrac{2x\cdot \color{red}\bm{(x+2)} \color{black}}{(x+2)^2(x-3)} + \cfrac{(4x-3)\cdot \color{blue} \bm{(x-3)} \color{black}}{(x+2)^2(x-3)}$

Wir verbinden nun die beiden algebraischen Brüche, da sie den gleichen Nenner haben:

$\cfrac{2x(x+2)-(4x-3)(x-3)}{(x+2)^2(x-3)}$

Und wir operieren mit dem Zähler. Wir lösen zunächst die Polynommultiplikationen:

$\cfrac{2x^2+4x-\bigl[4x^2-12x-3x+9\bigr]}{(x+2)^2(x-3)}$

Ein sehr häufiger Fehler beim Subtrahieren algebraischer Brüche ist das Vergessen, nach der Multiplikation Klammern zu setzen. Dies wäre ein Fehler, da sich das negative Vorzeichen auf alle resultierenden Elemente des Produkts auswirkt, nicht nur auf den ersten Term.

Wir führen die Operationen in Klammern aus:

$\cfrac{2x^2+4x-\bigl[4x^2-15x+9\bigr]}{(x+2)^2(x-3)}$

Dank des negativen Vorzeichens ändern wir also das Vorzeichen aller Terme in Klammern:

$\cfrac{2x^2+4x-4x^2+15x-9}{(x+2)^2(x-3)}$

Und schließlich gruppieren wir ähnliche Monome:

$\cfrac{-2x^2+19x-9}{(x+2)^2(x-3)}$

Multiplikation algebraischer Brüche

Um algebraische Brüche zu multiplizieren, faktorisieren wir zunächst alle Polynome dieser Brüche, multiplizieren dann die Zähler miteinander und die Nenner miteinander und vereinfachen schließlich den erhaltenen Bruch.

Daher wird das Produkt algebraischer Brüche tatsächlich auf die gleiche Weise berechnet wie das Produkt normaler Brüche.

Sehen wir uns als Nächstes anhand eines Beispiels an, wie man zwei algebraische Brüche multipliziert:

$\cfrac{3x}{x^2+x-2} \cdot \cfrac{x^2-6x+5}{x+1}$

Zunächst müssen Sie alle Polynome der Brüche faktorisieren, sowohl die Zähler als auch die Nenner:

$\cfrac{3x}{(x-1)(x+2)} \cdot \cfrac{(x-1)(x-5)}{x+1}$

Jetzt multiplizieren wir Brüche. Dazu multiplizieren wir Zähler und Nenner miteinander:

$\cfrac{3x \cdot (x-1)(x-5)}{(x-1)(x+2)\cdot (x+1)}$

$\cfrac{3x(x-1)(x-5)}{(x-1)(x+2)(x+1)}$

Und schließlich vereinfachen wir die Faktoren, die sich im Nenner und Zähler wiederholen:

$\cfrac{3x\cancel{(x-1)}(x-5)}{\cancel{(x-1)}(x+2)(x+1)}$

Das Ergebnis der Multiplikation ist also:

$\cfrac{3x(x-5)}{(x+2)(x+1)}$

Der Bruch kann nicht weiter vereinfacht werden. Damit sind wir bereits mit der Multiplikation algebraischer Brüche fertig.

Division algebraischer Brüche

Um eine Division algebraischer Brüche zu berechnen, faktorisieren wir zunächst alle Polynome, multiplizieren dann die Brüche transversal (den ersten Zähler mit dem zweiten Nenner und den ersten Nenner mit dem zweiten Zähler) und vereinfachen schließlich den algebraischen Bruch.

Sehen wir uns also anhand eines Beispiels genauer an, wie zwei algebraische Brüche dividiert werden:

$\cfrac{x^3-7x-6}{2x^2-8} : \cfrac{x^2+2x+1}{6}$

Der erste Schritt bei der Division zweier algebraischer Brüche besteht darin, alle an der Operation beteiligten Polynome zu faktorisieren:

$\cfrac{(x+1)(x+2)(x-3)}{2(x-2)(x+2)} : \cfrac{(x+1)^2}{6}$

Jetzt müssen wir die Brüche dividieren. Dazu multiplizieren wir die Brüche quer, das heißt, der erste Zähler wird mit dem zweiten Nenner multipliziert und das Ergebnis ist der Zähler des neuen Bruchs, und auf die gleiche Weise wird der erste Nenner mit dem zweiten Zähler multipliziert und das Ergebnis wird der Nenner des neuen Bruchs sein:

$\cfrac{(x+1)(x+2)(x-3)\cdot 6}{2(x-2)(x+2)\cdot (x+1)^2}$

$\cfrac{6(x+1)(x+2)(x-3)}{2(x-2)(x+2)(x+1)^2}$

Wir vereinfachen die Faktoren, die sich im Nenner und Zähler wiederholen:

$\cfrac{6\cancel{(x+1)}\cancel{(x+2)}(x-3)}{2(x-2)\cancel{(x+2)}(x+1)^\cancel{2}}$

$\cfrac{6(x-3)}{2(x-2)(x+1)}$

Und wir können den Bruch noch weiter vereinfachen, denn

$6:2 = 3.$

$\cfrac{3(x-3)}{(x-2)(x+1)}$

Der Bruch kann nicht weiter vereinfacht werden. Daher haben wir bereits algebraische Brüche dividiert.

Gelöste Übungen zu algebraischen Brüchen

Im Folgenden bieten wir Ihnen einige Übungen an, die Schritt für Schritt zu algebraischen Brüchen gelöst werden, damit Sie üben und das Konzept so vollständig verstehen können. Vergessen Sie nicht, dass Sie uns unten in den Kommentaren alle Fragen stellen können, die Sie haben! 💬💬💬

Übung 1

Bestimmen Sie, ob die folgenden algebraischen Brüche äquivalent sind:

$\cfrac{x+3}{x^2-9} \qquad \cfrac{1}{x-3} \qquad \cfrac{x-3}{x^2+2x-3}$

Sehen Sie sich die Lösung an

Um zu überprüfen, ob zwei algebraische Brüche äquivalent sind, müssen Sie sie transversal multiplizieren und prüfen, ob Sie eine Gleichheit erhalten. Wir prüfen also zunächst den ersten und zweiten Bruch:

$\cfrac{x+3}{x^2-9}= \cfrac{1}{x-3} \quad ?$

$(x+3)\cdot (x-3)=(x^2-9)\cdot 1$

Wir lösen die bemerkenswerte Identität auf der linken Seite der Gleichung:

$x^2-9=x^2-9$

✅

In diesem Fall haben wir eine Gleichheit erhalten, sodass der erste und der zweite Bruch algebraisch gleich sind.

Das gleiche Verfahren wenden wir nun mit dem ersten und dritten algebraischen Bruch an:

$\cfrac{x+3}{x^2-9}= \cfrac{x-3}{x^2+2x-3} \quad ?$

$(x+3)\cdot (x^2+2x-3)=(x^2-9)\cdot(x-3)$

$x^3+2x^2-3x+3x^2+6x-9=x^3-3x^2-9x+27$

$x^3+5x^2+3x-9=x^3-3x^2-9x+27$

❌

Allerdings erfüllen die algebraischen Brüche dieses Mal die Gleichung nicht, sodass der erste und der dritte Bruch mathematisch unterschiedlich sind.

Zusammenfassend lässt sich sagen, dass sich der dritte Bruch vom ersten Bruch unterscheidet und daher auch ungleich dem zweiten Bruch ist, da der erste und der zweite Bruch gleichwertig sind.

$\cfrac{x+3}{x^2-9} = \cfrac{1}{x-3} \neq \cfrac{x-3}{x^2+2x-3}$

Übung 2

Vereinfachen Sie die folgenden algebraischen Brüche:

$\text{A)} \ \cfrac{5x^2+10x}{11x}$

$\text{B)} \ \cfrac{x^2-4}{x^2+2x-8}$

$\text{C)} \ \cfrac{x^3-2x^2-3x}{x^2-3x}$

$\text{D)} \ \cfrac{x^3-3x+2}{x^3+4x^2+x-6}$

Sehen Sie sich die Lösung an

Um einen algebraischen Bruch zu vereinfachen, müssen wir die Polynome im Zähler und Nenner faktorisieren und dann die wiederholten Faktoren eliminieren. Noch:

$\text{A)} \ \begin{array}{l} \cfrac{5x^2+10x}{11x} =\cfrac{5x(x+2)}{11x} = \\[4ex] =\cfrac{5\cancel{x}(x+2)}{11\cancel{x}}= \cfrac{\bm{5(x+2)}}{\bm{11}}\end{array}$

$\text{B)} \ \begin{array}{l} \cfrac{x^2-4}{x^2+2x-8} = \cfrac{(x-2)(x+2)}{(x-2)(x+4)}= \\[4ex] = \cfrac{\cancel{(x-2)}(x+2)}{\cancel{(x-2)}(x+4)}=\cfrac{\bm{x+2}}{\bm{x+4}}}\end{array}$

$\text{C)} \ \begin{array}{l} \cfrac{x^3-2x^2-3x}{x^2-3x} = \cfrac{x(x+1)(x-3)}{x(x-3)}}= \\[4ex] = \cfrac{\cancel{x} (x+1) \cancel{x-3}}{\cancel{x}\cancel{(x-3)}} = \cfrac{x+1}{1} = \\[4ex] = \bm{x+1}\end{array}$

$\text{D)} \ \begin{array}{l} \cfrac{x^3-3x+2}{x^3+4x^2+x-6}=\cfrac{(x-1)^2(x+2)}{(x-1)(x+3)(x+2)}= \\[4ex] = \cfrac{(x-1)^{\cancel{2}}\cancel{(x+2)}}{\cancel{(x-1)}(x+3)\cancel{(x+2)}}=\cfrac{\bm{x-1}}{\bm{x+3}}\end{array}$

Übung 3

Berechnen Sie die folgenden Additionen und Subtraktionen algebraischer Brüche:

$\text{A)} \ \cfrac{4}{x^2+2x} + \cfrac{3x-2}{x^2-x-6}$

$\text{B)} \ \cfrac{4x}{x^3+2x^2+x} - \cfrac{2}{x^2-3x-4}$

$\text{C)} \ \cfrac{7x}{x^2-4x+4} + \cfrac{-5}{x-2}$

$\text{D)} \ x +\cfrac{-3x}{x^2-4} - \cfrac{2x^3-1}{2x^2+6x+4}$

Sehen Sie sich die Lösung an

Um algebraische Brüche zu addieren (oder zu subtrahieren), müssen wir zunächst die Brüche auf einen gemeinsamen Nenner reduzieren und dann die Zähler addieren (oder subtrahieren). ALSO:

$\text{A)} \ \begin{array}{l} \cfrac{4}{x^2+2x} + \cfrac{3x-2}{x^2-x-6} = \cfrac{4}{x(x+2)} + \cfrac{3x-2}{(x+2)(x-3)} = \\[4ex] =\cfrac{4\cdot(x-3)}{x(x+2)\cdot (x-3)} + \cfrac{(3x-2)\cdot x}{(x+2)(x-3)\cdot x} = \cfrac{4\cdot(x-3) + (3x-2)\cdot x}{x(x+2)(x-3)} = \\[4ex] = \cfrac{4x-12 + 3x^2-2x}{x(x+2)(x-3)} = \cfrac{ \bm{3x^2+2x-12}}{\bm{x(x+2)(x-3)}} \end{array}$

$\text{B)} \ \begin{array}{l} \cfrac{4x}{x^3+2x^2+x} - \cfrac{2}{x^2-3x-4} = \cfrac{4x}{x(x+1)^2} - \cfrac{2}{(x+1)(x-4)}= \\[4ex] = \cfrac{4x \cdot (x-4)}{x(x+1)^2 \cdot (x-4)} - \cfrac{2 \cdot (x+1) \cdot x}{(x+1)^2(x-4)\cdot x}= \cfrac{4x \cdot (x-4) - 2 \cdot (x+1) \cdot x }{x(x+1)^2 (x-4) }= \\[4ex] = \cfrac{4x^2 -16x - 2 \cdot (x^2+x) }{x(x+1)^2 (x-4) }= \cfrac{4x^2 -16x - 2x^2 - 2x }{x(x+1)^2 (x-4) } =\\[4ex] =\cfrac{2x^2 -18x}{x(x+1)^2 (x-4)}=\cfrac{x(2x -18)}{x(x+1)^2 (x-4)}= \\[4ex] = \cfrac{\bm{2x -18}}{\bm{(x+1)^2 (x-4)}}\end{array}$

$\text{C)} \ \begin{array}{l}\cfrac{7x}{x^2-4x+4} + \cfrac{-5}{x-2}=\cfrac{7x}{(x-2)^2} + \cfrac{-5}{x-2}} = \\[4ex] = \cfrac{7x}{(x-2)^2} + \cfrac{-5\cdot (x-2)}{(x-2)\cdot (x-2)}=\cfrac{7x}{(x-2)^2} + \cfrac{-5\cdot (x-2)}{(x-2)^2}= \\[4ex] = \cfrac{7x + [-5\cdot (x-2)] }{(x-2)^2} =\cfrac{7x -5\cdot (x-2) }{(x-2)^2} = \\[4ex] = \cfrac{7x -5x+10 }{(x-2)^2} = \cfrac{ \bm{2x+10}}{\bm{(x-2)^2 } } \end{array}$

$\text{D)} \ \begin{array}{l} x +\cfrac{-3x}{x^2-4} - \cfrac{2x^3-1}{2x^2+6x+4}=\cfrac{x}{1} +\cfrac{-3x}{x^2-4} - \cfrac{2x^3-1}{2x^2+6x+4}= \\[4ex] =x +\cfrac{-3x}{(x-2)(x+2)} - \cfrac{2x^3-1}{2(x+1)(x+2)}= \\[4ex] = \cfrac{x\cdot 2(x-2)(x+2)(x+1)}{1\cdot 2(x-2)(x+2)(x+1)} \ + \ \cfrac{-3x\cdot 2(x+1)}{(x-2)(x+2)\cdot 2(x+1)} \ - \ \cfrac{(2x^3-1)\cdot(x-2)}{2(x+1)(x+2)\cdot (x+1)}= \\[4ex] = \cfrac{ 2x(x-2)(x+2)(x+1)}{2(x-2)(x+2)(x+1)} \ + \ \cfrac{-6x(x+1)}{2(x-2)(x+2)(x+1)} \ - \ \cfrac{(2x^3-1)\cdot(x-2)}{2(x-2)(x+2)(x+1)}= \\[4ex]= \cfrac{ 2x^4+2x^3-8x^2-8x}{2(x-2)(x+2)(x+1)} \ + \ \cfrac{-6x^2-6x}{2(x-2)(x+2)(x+1)} \ - \ \cfrac{2x^4-4x^3-x+2}{2(x-2)(x+2)(x+1)} = \\[4ex] = \cfrac{ 2x^4+2x^3-8x^2-8x -6x^2-6x - (2x^4-4x^3-x+2)}{2(x-2)(x+2)(x+1)} = \\[4ex] = \cfrac{ 2x^4+2x^3-8x^2-8x -6x^2-6x - 2x^4+4x^3+x-2}{2(x-2)(x+2)(x+1)} = \\[4ex] = \cfrac{ \bm{6x^3-14x^2-13x-2}}{\bm{2(x-2)(x+2)(x+1)}}\end{array}$

Übung 4

Lösen Sie die folgenden Multiplikationen und Divisionen algebraischer Brüche:

$\text{A)} \ \cfrac{x^2+5x+4}{7}\cdot \cfrac{x-1}{x^2-1}$

$\text{B)} \ \cfrac{3x^2+15x+18}{3x}\cdot \cfrac{x^2+x-2}{x^3+3x^2-x-3}$

$\text{C)} \ \cfrac{3x}{x^2+10x+25}:\cfrac{2x}{x^2-25}$

$\text{D)} \ \cfrac{x^2+8x+15}{4x}:\cfrac{x^2+4x-5}{2x^2}$

Sehen Sie sich die Lösung an

Um algebraische Brüche zu multiplizieren, müssen wir zunächst alle Polynome faktorisieren, dann die Zähler und Nenner miteinander multiplizieren und schließlich den resultierenden Bruch vereinfachen.

$\text{A)} \ \begin{array}{l} \cfrac{x^2+5x+4}{7}\cdot \cfrac{x-1}{x^2-1} = \cfrac{(x+1)(x+4)}{7}\cdot \cfrac{x-1}{(x-1)(x+1)}\\[4ex] =\cfrac{(x+1)(x+4)\cdot (x-1)}{7 \cdot (x-1)(x+1)}=\cfrac{(x+1)(x+4) (x-1)}{7(x-1)(x+1)} = \\[4ex] = \cfrac{\cancel{(x+1)}(x+4)\cancel{ (x-1)}}{7\cancel{(x-1)}\cancel{(x+1)}} = \cfrac{\bm{x+4}}{\bm{7}}\end{array}$

$\text{B)} \ \begin{array}{l}\cfrac{3x^2+15x+18}{3x}\cdot \cfrac{x^2+x-2}{x^3+3x^2-x-3} = \cfrac{3(x+2)(x+3)}{3x}\cdot \cfrac{(x-1)(x+2)}{(x-1)(x+1)(x+3)}= \\[4ex] =\cfrac{3(x+2)(x+3)\cdot (x-1)(x+2)}{3x\cdot (x-1)(x+1)(x+3)}=\cfrac{3(x+2)(x+3) (x-1)(x+2)}{3x (x-1)(x+1)(x+3)} = \\[4ex] = \cfrac{\cancel{3}(x+2)\cancel{(x+3)} \cancel{(x-1)}(x+2)}{\cancel{3}x \cancel{(x-1)}(x+1)\cancel{(x+3)}} = \cfrac{(x+2)(x+2)}{x (x+1)} = \\[4ex] = \cfrac{\bm{(x+2)^2}}{\bm{x (x+1)}}\end{array}$

Um hingegen algebraische Brüche zu dividieren, faktorisieren wir zunächst alle Polynome, multiplizieren dann die Brüche transversal (den ersten Zähler mit dem zweiten Nenner und den ersten Nenner mit dem zweiten Zähler) und vereinfachen schließlich den gefundenen algebraischen Bruch.

$\text{C)} \ \begin{array}{l} \cfrac{3x}{x^2+10x+25}:\cfrac{2x}{x^2-25}= \cfrac{3x}{(x+5)^2}:\cfrac{2x}{(x-5)(x+5)}=\\[4ex] = \cfrac{3x\cdot (x-5)(x+5)}{(x+5)^2\cdot 2x}=\cfrac{3x(x-5)(x+5)}{2x(x+5)^2 }= \\[4ex] =\cfrac{3\cancel{x}(x-5)\cancel{(x+5)}}{2\cancel{x}(x+5)^\cancel{2}} = \cfrac{\bm{3(x-5)}}{\bm{2(x+5)}}\end{array}$

$\text{D)} \ \begin{array}{l} \cfrac{x^2+8x+15}{4x}:\cfrac{x^2+4x-5}{2x^2} = \cfrac{(x+3)(x+5)}{4x}:\cfrac{(x-1)(x+5)}{2x^2}= \\[4ex] = \cfrac{(x+3)(x+5)\cdot 2x^2 }{4x \cdot (x-1)(x+5)} = \cfrac{2x^2 (x+3)(x+5)}{4x (x-1)(x+5)} = \\[4ex] = \cfrac{2x^{\cancel{2}}(x+3)\cancel{ (x+5)}}{4\cancel{x} (x-1)\cancel{ (x+5)}} =\cfrac{2x(x+3)}{4(x-1)} = \cfrac{\bm{x(x+3)}}{\bm{2(x-1)}}\end{array}$

Was halten Sie von der Erklärung? Hat es Ihnen gefallen? Oder habt ihr Vorschläge? 💬 Sagen Sie uns in den Kommentaren, was Sie von dieser Seite halten! Wir lesen euch alle! 👀 Und vergessen Sie nicht, dass Sie uns auch alle Ihre Fragen stellen können! ❔👇❔👇

Algebraische brüche: vereinfachung, operationen, gelöste aufgaben,…

Was sind algebraische Brüche?

Algebraisches Bruchäquivalent

Vereinfachen Sie algebraische Brüche

Operationen mit algebraischen Brüchen

Algebraische Brüche addieren und subtrahieren

Algebraische Brüche addieren

Subtraktion algebraischer Brüche

Multiplikation algebraischer Brüche

Division algebraischer Brüche

Gelöste Übungen zu algebraischen Brüchen

Übung 1

Übung 2

Übung 3

Übung 4

Kommentar verfassen Kommentieren abbrechen