Operationen mit monomen

Auf dieser Seite erklären wir, wie man alle Operationen mit Monomen (Addition, Subtraktion, Multiplikation, Division und Potenz) durchführt. Darüber hinaus können Sie Beispiele für jede Art von Operation mit Monomen sehen und anhand von Übungen üben, die Schritt für Schritt gelöst werden.

Addition und Subtraktion von Monomen

Zwei oder mehr Monome können nur dann addiert oder subtrahiert werden, wenn es sich um ähnliche Monome handelt, das heißt, wenn die beiden Monome einen identischen Literalteil haben (gleiche Buchstaben und gleiche Exponenten).

Dann ist die Summe (oder Subtraktion) zweier ähnlicher Monome gleich einem anderen Monom, das aus demselben Literalteil und der Summe (oder Subtraktion) der Koeffizienten dieser beiden Monome besteht.

Addition und Subtraktion von Monomen werden auch als Addition bzw. Subtraktion von Monomen bezeichnet.

Beispiele für Addition und Subtraktion von Monomen

Damit Sie klar verstehen, wie man zwei oder mehr Monome addiert und subtrahiert, hinterlassen wir Ihnen unten einige Beispiele:

• 

• 

• 

• 

• 

Die Monome im letzten Beispiel können nicht addiert oder subtrahiert werden, da sie nicht ähnlich sind oder, mit anderen Worten, unterschiedliche Unbekannte oder Exponenten haben.

Produkt einer Zahl mit einem Monom

Um das Produkt eines Monoms mit einer Zahl zu lösen, multiplizieren Sie einfach den Koeffizienten des Monoms mit dieser Zahl, wobei der Literalteil des Monoms gleich bleibt.

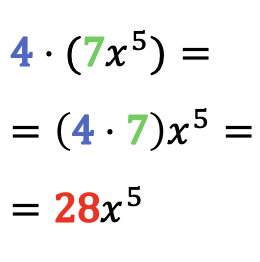
Beispiele für die Multiplikation von Zahlen mit Monomen

• 

• 

• 

• 

Multiplikation von Monomen

Das Ergebnis der Multiplikation zweier Monome ist ein weiteres Monom, dessen Koeffizient das Produkt der Koeffizienten der Monome ist und dessen Literalteil durch Multiplikation der Variablen mit derselben Basis, also durch Addition ihrer Exponenten, erhalten wird.

Um zwei verschiedene Monome zu multiplizieren, müssen wir daher die Koeffizienten zwischen ihnen multiplizieren und die Exponenten der Potenzen mit derselben Basis addieren.

Wenn wir jedoch zwei Monome mit unterschiedlichen Basispotenzen multiplizieren , müssen wir einfach ihre Koeffizienten miteinander multiplizieren und die Potenzen gleich lassen. Zum Beispiel:

Andererseits muss bei der Multiplikation von Monomen die Vorzeichenregel beachtet werden:

• Ein positives Monom multipliziert mit einem positiven Monom ergibt ein weiteres positives Monom.
• Ein positives Monom multipliziert mit einem negativen Monom (oder umgekehrt) ergibt ein negatives Monom.
• Zwei negative Monome miteinander multipliziert ergeben ein positives Monom.

Beispiele für Monommultiplikationen

Nachfolgend finden Sie einige Beispiele für die Multiplikation zwischen Monomen, damit Sie sehen können, wie sie durchgeführt wird:

• 

• 

• 

• 

• 

Wie Sie gesehen haben, ist die Lösung einer Multiplikation von Monomen relativ einfach. Sie sollten jedoch bedenken, dass Monome auch mit Polynomen multipliziert werden können, und sogar zwei oder mehr Polynome können miteinander multipliziert werden. Wenn Sie mehr Interesse haben, können Sie sehen, wie all diese Operationen funktionieren, indem Sie auf Polynommultiplikation klicken.

Division von Monomen

In der Mathematik ist das Ergebnis der Division von Monomen ein weiteres Monom, dessen Koeffizient dem Quotienten der Koeffizienten der Monome entspricht und dessen Literalteil durch Division der Variablen mit derselben Basis, also durch Subtraktion ihrer Exponenten, erhalten wird .

Natürlich kann jede Division von Monomen auch als Bruch ausgedrückt werden:

Wie bei der Multiplikation ist auch bei der Division von Monomen das Zeichengesetz anzuwenden:

• Ein positives Monom dividiert durch ein positives Monom ergibt ein weiteres positives Monom.
• Ein positives Monom dividiert durch ein negatives Monom (oder umgekehrt) ist äquivalent zu einem negativen Monom.
• Zwei durcheinander dividierte negative Monome ergeben ein positives Monom.

Beispiele für die Division von Monomen

Weitere Beispiele für die Division von zwei oder mehr Monomen finden Sie unten:

• 

• 

• 

• 

• 

Sicherlich haben Sie sich irgendwann, wenn Sie etwas Neues in Mathematik gelernt haben, gefragt: Wozu dient es ? Nun, die Monomdivision wird verwendet, um Polynome zu dividieren. Tatsächlich kommt es recht häufig vor, dass man bei der Division von Polynomen einen Fehler macht, weil zwei Monome falsch dividiert wurden. Aus diesem Grund empfehlen wir Ihnen, nachdem Sie mit der Division zwischen Monomen vertraut sind, zu sehen, wie die Division von Polynomen berechnet wird, da es Ihnen jetzt viel leichter fallen wird, das Verfahren zu erlernen (es ist ziemlich kompliziert).

Potenz eines Monoms

In der Mathematik wird zur Berechnung der Potenz eines Monoms jedes Element des Monoms auf den Exponenten der Potenz erhöht . Mit anderen Worten: Die Potenz eines Monoms besteht darin, seinen Koeffizienten und seine Variablen (Buchstaben) auf den Exponenten der Potenz zu erhöhen.

Bedenken Sie bei den Eigenschaften von Potenzen, dass sich die Exponenten vervielfachen, wenn beide einen bereits hohen Term erhöhen. Aus diesem Grund wird bei der Potenz eines Monoms der Exponent jedes Buchstabens immer mit dem Exponenten multipliziert, der die Potenz angibt .

Um diesen Vorgang korrekt durchzuführen, müssen Sie andererseits die folgende Eigenschaft der Kräfte beachten:

• Ein negatives Monom, das auf einen geraden Exponenten erhöht wird, entspricht einem positiven Monom.
• Stattdessen ergibt ein negatives Monom, das auf einen ungeraden Exponenten erhöht wird, ein negatives Monom.

Beispiele für Potenzen von Monomen

Wir überlassen Ihnen einige Beispiele, damit Sie klar verstehen, wie die Potenz eines Monoms berechnet wird:

• 

• 

• 

• 

• 

Operationen kombiniert mit Monomen

Nachdem Sie alle Operationen mit Monomen gesehen haben, wissen Sie, dass sie auch miteinander kombiniert werden können. Das heißt, wir können Übungen finden, in denen wir aufgefordert werden, Operationen mit Monomen zu lösen, an denen alle Arten beteiligt sind: Addition, Subtraktion, Multiplikation, Division und Potenzen.

Aber keine Sorge, sie sind nicht so schwierig, wie sie scheinen. Das Einzige, was Sie sich merken müssen, ist die Reihenfolge, in der die kombinierten Vorgänge gelöst werden:

1. Zunächst werden Operationen mit Monomen in Klammern gelöst.
2. Dann werden die Potenzen der Monome berechnet.
3. Drittens werden Multiplikationen und Divisionen von Monomen durchgeführt.
4. Und schließlich werden die Additionen und Subtraktionen von Monomen bestimmt.

Ich bin sicher, dass Sie es klarer sehen werden, wenn Sie ein Beispiel lösen:

Beispiel für die kombinierte Operation von Monomen

Zunächst müssen wir die Operationen mit Monomen in Klammern lösen:

In diesem Fall haben wir keine Macht. Berechnen wir nun die Multiplikationen und Divisionen von Monomen:

Und schließlich addieren und subtrahieren wir Monome:

Aufgaben zu Operationen mit Monomen gelöst

Für den Fall, dass Sie üben möchten, stellen wir Ihnen nachfolgend einige Schritt-für-Schritt-Übungen zur ESO-Schwierigkeitsstufe für Operationen mit Monomen vor.

Übung 1

Berechnen Sie die folgenden Additionen und Subtraktionen von Monomen:

Übung 2

Lösen Sie die folgenden Multiplikationen von Monomen: