In diesem Artikel erfahren Sie, wie Sie die Differenzierbarkeit einer Funktion untersuchen, also ob eine Funktion differenzierbar ist oder nicht. Darüber hinaus werden wir den Zusammenhang zwischen Differenzierbarkeit und Stetigkeit einer Funktion sehen. Und schließlich werden wir die Differenzierbarkeit einer stückweisen Funktion untersuchen.
Differenzierbarkeit und Stetigkeit einer Funktion
Die Stetigkeit und Differenzierbarkeit einer Funktion an einem Punkt hängen wie folgt zusammen:
- Wenn eine Funktion an einem Punkt differenzierbar ist, ist die Funktion an diesem Punkt stetig.
- Wenn eine Funktion an einem Punkt nicht stetig ist, ist sie an diesem Punkt auch nicht differenzierbar.
Die Umkehrung dieses Theorems ist jedoch falsch: Nur weil eine Funktion an einem Punkt stetig ist, heißt das nicht, dass sie an diesem Punkt immer differenzierbar ist.
Sie können auch anhand ihrer grafischen Darstellung erkennen, ob eine Funktion an einem Punkt differenzierbar ist oder nicht:
- Handelt es sich um einen glatten Punkt, ist die Funktion an diesem Punkt differenzierbar.
- Handelt es sich um einen Winkelpunkt, ist die Funktion an diesem Punkt stetig, aber nicht differenzierbar.

Glättungspunkt bei x=0:
kontinuierliche und differenzierbare Funktion in diesem Stadium.

Winkelpunkt bei x=2:
Funktion stetig, aber zu diesem Zeitpunkt nicht differenzierbar.
Differenzierbarkeit einer stückweisen Funktion
Sobald wir die Beziehung zwischen Stetigkeit und Differenzierbarkeit einer Funktion kennen, werden wir sehen, wie wir die Differenzierbarkeit einer stückweise definierten Funktion untersuchen können.
Sie können feststellen, ob eine stückweise Funktion an einem Punkt differenzierbar ist, indem Sie die lateralen Ableitungen an diesem Punkt berechnen:
- Wenn die lateralen Ableitungen an einem Punkt ungleich sind, ist die Funktion an diesem Punkt nicht differenzierbar:
![]()
Es ist nicht abzugsfähig
![]()
- Wenn die lateralen Ableitungen an einem Punkt zusammenfallen, ist die Funktion an diesem Punkt differenzierbar:
![]()
Ja, es ist differenzierbar in
![]()
Hinweis: Damit eine Funktion an einem Punkt differenzierbar ist, muss die Funktion an diesem Punkt stetig sein. Daher müssen wir vor der Berechnung der lateralen Ableitungen sicherstellen, dass die Funktion an diesem Punkt stetig ist. Wenn Sie nicht wissen, wie Kontinuität an einem Punkt untersucht wird, können Sie unter folgendem Link sehen, wie es gemacht wird:
Sehen wir uns nun ein Beispiel an, wie man die Ableitung einer Funktion berechnet, die stückweise an einem Punkt definiert ist:
- Untersuchen Sie die Stetigkeit und Differenzierbarkeit der folgenden Funktion, die stückweise am Punkt x=2 definiert ist:
![Rendered by QuickLaTeX.com \displaystyle f(x)= \left\{ \begin{array}{lcl} 3x^2-6x & \text{si} & x<2 \\[2ex] 6\ln (x-1) & \text{si} & x\geq 2 \end{array} \right.](https://mathority.org/wp-content/ql-cache/quicklatex.com-a98eee72521c68fd394eb6209a7d0a59_l3.png)
Die Funktionen der beiden Teile sind in ihren jeweiligen Intervallen stetig, es muss jedoch geprüft werden, ob die Funktion am kritischen Punkt x=2 stetig ist. Dazu lösen wir die seitlichen Grenzen der Funktion im Punkt:
![]()
![]()
Die seitlichen Grenzen am kritischen Punkt lieferten das gleiche Ergebnis, sodass die Funktion am Punkt x=2 stetig ist.
Sobald wir wissen, dass die Funktion bei x=2 stetig ist, werden wir die Differenzierbarkeit der Funktion an diesem Punkt untersuchen. Dazu berechnen wir die lateralen Ableitungen der in Stücken definierten Funktion:
![Rendered by QuickLaTeX.com \displaystyle f'(x)= \left\{ \begin{array}{lcl} 6x-6 & \text{si} & x<2 \\[2ex] \cfrac{6}{x-1} & \text{si} & x\geq 2 \end{array} \right.](https://mathority.org/wp-content/ql-cache/quicklatex.com-3709995609d0f69f382ff651e397c00a_l3.png)
Wir bewerten nun jede laterale Ableitung am kritischen Punkt:
![]()
![]()
Die beiden lateralen Ableitungen lieferten das gleiche Ergebnis, sodass die Funktion bei x=2 differenzierbar ist und der Wert der Ableitung 6 beträgt:
![]()
Hätten uns die lateralen Ableitungen andererseits ein anderes Ergebnis geliefert, würde dies bedeuten, dass die Funktion bei x=2 nicht differenzierbar ist. Mit anderen Worten: Die Ableitung würde zu diesem Zeitpunkt noch nicht existieren.
Denken Sie abschließend daran, dass dieses Verfahren auch für die Untersuchung der Differenzierbarkeit einer Absolutwertfunktion gilt, da Absolutwertfunktionen auch stückweise definiert werden können. Hier können Sie sehen, wie Sie eine Absolutwertfunktion in Chunks umwandeln:
➤ Siehe: So definieren Sie stückweise eine Funktion mit einem Absolutwert
Gelöste Übungen zur Differenzierbarkeit einer Funktion
Übung 1
Untersuchen Sie die Stetigkeit und Differenzierbarkeit der folgenden stückweisen Funktion:
![Rendered by QuickLaTeX.com \displaystyle f(x)= \left\{ \begin{array}{lcl} x^3-4x^2 + 5 & \text{si} & x<1 \\[2ex] -x^2+3x & \text{si} & x\geq 1 \end{array} \right.](https://mathority.org/wp-content/ql-cache/quicklatex.com-3656065bb8de98bd07da153f26fd326e_l3.png)
Die Funktionen der beiden Teile sind stetig, wir müssen jedoch prüfen, ob die Funktion am kritischen Punkt x=1 stetig ist. Dazu lösen wir die seitlichen Grenzen der Funktion im Punkt:
![]()
![]()
Die beiden seitlichen Grenzen am kritischen Punkt ergeben das gleiche Ergebnis, sodass die Funktion bei x=1 stetig ist.
Sobald wir wissen, dass die Funktion am kritischen Punkt stetig ist, werden wir untersuchen, ob sie am selben Punkt differenzierbar ist. Wir berechnen daher die lateralen Ableitungen:
![Rendered by QuickLaTeX.com \displaystyle f'(x)= \left\{ \begin{array}{lcl} 3x^2-8x & \text{si} & x<1 \\[2ex] -2x+3 & \text{si} & x\geq 1 \end{array} \right.](https://mathority.org/wp-content/ql-cache/quicklatex.com-42451fa799527167fe9a2e2259248870_l3.png)
Und wir werten die beiden lateralen Ableitungen bei x=1 aus;
![]()
![]()
Die lateralen Ableitungen fallen im Punkt x=1 nicht zusammen, sodass die Funktion an diesem Punkt nicht differenzierbar ist.
![]()
Übung 2
Analysieren Sie die Differenzierbarkeit und Stetigkeit der folgenden in Abschnitten definierten Funktion:
![\displaystyle f(x)= \left\{ \begin{array}{lcl} \sqrt{4x} & \text{si} & x\leq 1 \\[2ex] 2+\ln x & \text{si} & x> 1 \end{array} \right.“ title=“Rendered by QuickLaTeX.com“ height=“65″ width=“226″ style=“vertical-align: 0px;“></p>
</p>
<div class=](https://mathority.org/wp-content/ql-cache/quicklatex.com-0d118e3904c810abd15e427e9c7d0504_l3.png)
![Rendered by QuickLaTeX.com \displaystyle f'(x)= \left\{ \begin{array}{lcl} \cfrac{4}{2\sqrt{4x}} & \text{si} & x<1 \\[4ex] \cfrac{1}{x} & \text{si} & x\geq 1 \end{array} \right.](https://mathority.org/wp-content/ql-cache/quicklatex.com-8261f3d268b47d9171710997c8cc70bd_l3.png)
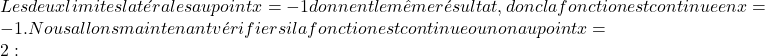
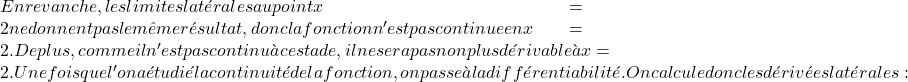
^2 & \text{si} & x\geq 3 \end{array} \right.](https://mathority.org/wp-content/ql-cache/quicklatex.com-ce34d5d8a949fb3a0b904e9bf7d32f5b_l3.png)
![Rendered by QuickLaTeX.com \displaystyle f'(x)= \left\{ \begin{array}{lcl} 2e^{x-3} & \text{si} & x< 3 \\[2ex]2(x-b) & \text{si} & x\geq 3 \end{array} \right.](https://mathority.org/wp-content/ql-cache/quicklatex.com-d542fc9488644f0c144059ae1403d961_l3.png)