Hier finden Sie die Formel für die Ableitung des Arkuskotangens und wir erklären anhand von Beispielen, wie Sie den Arkuskotangens einer Funktion ableiten.
Arkuskotangens-Ableitungsformel
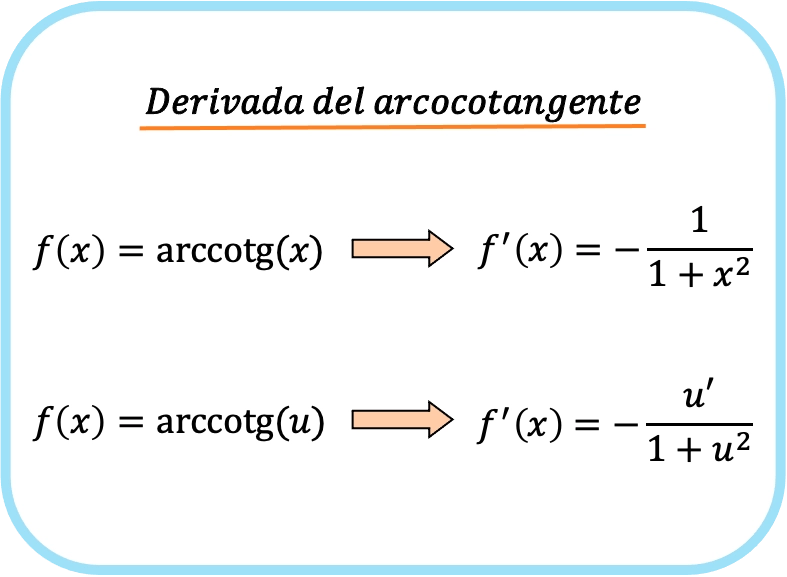
Die Ableitung des Arkustangens von x ist negativ eins dividiert durch eins plus x im Quadrat.
![]()
Daher ist die Ableitung des Arkuskotangens einer Funktion gleich minus der Ableitung dieser Funktion dividiert durch eins plus der quadrierten Funktion.
![]()
Beachten Sie, dass die erste und zweite Formel gleich sind. Der einzige Unterschied besteht darin, dass die Kettenregel auf den zweiten Ausdruck angewendet wird. Wenn Sie u durch ein x ersetzen, erhalten Sie tatsächlich die erste Formel, da die Ableitung der Funktion x 1 ist.
Obwohl der Arkuskotangens die Umkehrfunktion des Kotangens ist, sind ihre Ableitungen sehr unterschiedlich. Tatsächlich gibt es drei Möglichkeiten, den Kotangens einer Funktion abzuleiten. Sie können sie alle hier sehen:
➤ Siehe: Formel für die Ableitung des Kotangens
Beispiele für die Ableitung des Arkuskotangens
Nachdem wir gesehen haben, wie die Formel für die Ableitung des Arkuskotangens lautet, finden Sie hier zwei gelöste Übungen zu dieser Art trigonometrischer Ableitung. Denken Sie auch daran, dass Sie Ihre Frage unten in den Kommentaren hinterlassen können, wenn Sie Fragen haben.
Beispiel 1
In diesem Beispiel werden wir sehen, wie groß die Ableitung des Arkuskotangens der quadratischen Funktion x 2 ist.
![]()
Im Argument des Arkuskotangens haben wir eine andere Funktion als x, daher müssen wir die Formel für die Ableitung des Arkuskotangens mit der Kettenregel anwenden:
![]()
Die Ableitung von x erhöht auf zwei ist 2x, also müssen wir in den Zähler 2x und in den Nenner die Funktion des quadrierten Arguments setzen:
![]()
Beispiel 2
In diesem zweiten Beispiel werden wir den Arkuskotangens einer Polynomfunktion dritten Grades ableiten.
![]()
Zur Ableitung verwenden wir die Arkuskotangens-Ableitungsregel:
![]()
Die Ableitung des Arkuskotangens der Funktion ist also:
![]()