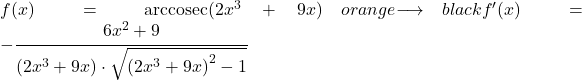Auf dieser Seite sehen Sie, wie die Formel für die Ableitung des Arkuskosekans lautet. Darüber hinaus können Sie gelöste Aufgaben zu Ableitungen des Arkuskosekans einer Funktion sehen.
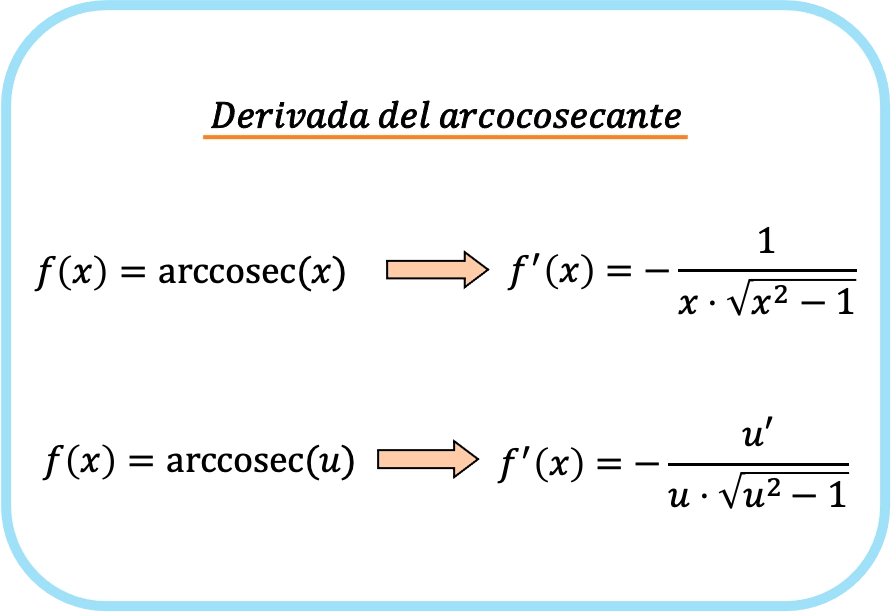
Arckosekant-Ableitungsformel
Die Ableitung des Arkuskosekans von x ist negativ eins über dem Produkt aus x mal der Wurzel von x zum Quadrat minus 1.
![]()
Daher ist die Ableitung des Arkuskosekants einer Funktion gleich minus dem Quotienten aus der Ableitung dieser Funktion dividiert durch die Funktion mal der Wurzel dieser Funktion zum Quadrat minus eins.
![]()
Tatsächlich sind die beiden vorherigen Formeln gleich, aber im zweiten Ausdruck wird die Kettenregel angewendet. Wenn Sie die Identitätsfunktion x in u einsetzen, erhalten Sie tatsächlich die Ableitung des Arkuskosekans von x, da die Ableitung von x eins ist.
Wie Sie wissen, ist der Arkuskosekans die umgekehrte trigonometrische Funktion des Kosekans, seine Ableitungen sind jedoch recht unterschiedlich. Die Formel für diese andere Art trigonometrischer Funktion finden Sie unter folgendem Link:
➤ Siehe: Ableitung des Kosekans
Beispiele für die Ableitung des Kosekansbogens
Nachdem wir gesehen haben, was die Arkuskosekans-Ableitungsregel ist, werden wir als Nächstes zwei Beispiele dieser Art von Ableitung lösen. Wenn Sie jedoch noch Fragen zur Ableitung des Kosekansbogens haben, können Sie uns diese in den Kommentaren stellen.
Beispiel 1
In diesem Beispiel werden wir sehen, wie groß die Ableitung des Arkuskosekans der quadratischen Funktion x 2 ist.
![]()
Um die Ableitung des Arkuskosekans von x im Quadrat zu berechnen, wenden wir die Formel an, die wir oben gesehen haben:
![]()
Die Ableitung von x hoch zwei ist 2x, daher ist die Ableitung der zusammengesetzten Funktion:
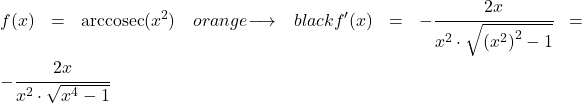
Beispiel 2
In diesem zweiten Beispiel werden wir den Arkuskosekans einer Potentialfunktion ableiten.
![]()
Wir müssen die Arcsecant-Ableitungsregel verwenden, um die Ableitung der gesamten Funktion zu finden.
![]()
Also schreiben wir in den Zähler die Ableitung des Arguments der Funktion, und in den Nenner schreiben wir die potentielle Funktion um und multiplizieren sie mit der Quadratwurzel der Funktion des Arguments zum Quadrat minus 1: