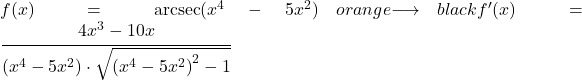Auf dieser Seite sehen Sie, was die Ableitung des Arcsecant (Formel) ist. Hier finden Sie gelöste Aufgaben zu Ableitungen des Arcussecans einer Funktion.
Arcsecant-Ableitungsformel
Die Ableitung des Arcsecans von x ist eins über das Produkt von x mal der Wurzel von x zum Quadrat minus 1.
![]()
Daher ist die Ableitung des Arcsecans einer Funktion gleich dem Quotienten aus der Ableitung dieser Funktion dividiert durch die Funktion mal der Wurzel dieser Funktion zum Quadrat minus eins.
![]()
Offensichtlich ähnelt die zweite Formel der ersten Formel. Der einzige Unterschied zwischen beiden besteht darin, dass in der zweiten Formel die Kettenregel angewendet wird.

Obwohl es seltsam erscheinen mag, weil es sich um Umkehrfunktionen handelt, hat die Ableitung des Arcsecans nichts mit der Ableitung des Sekantes zu tun. Sie können die Formel für die Ableitung der Sekante sehen, indem Sie hier klicken:
➤ Siehe:Ableitung der Sekante
Beispiele für Arcsecant-Derivate
Beispiel 1
In diesem Beispiel werden wir sehen, wie groß die Ableitung des Arcsecans der linearen Funktion 7x ist.
![]()
Um die Ableitung des Arcsecants zu finden, müssen Sie die entsprechende Formel anwenden, die wie folgt lautet:
![]()
Die Ableitung der 7x-Funktion ist 7, daher ist die Ableitung des Arcsecans der 7x-Funktion:
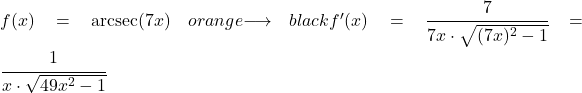
Beispiel 2
In diesem zweiten Beispiel werden wir den Arcsecans einer potentiellen Funktion ableiten.
![]()
Da das Argument der Arcsecant-Funktion einen anderen Term als x enthält, müssen wir die Arcsecant-Ableitungsregel mit der Kettenregel anwenden, um die gesamte Funktion abzuleiten.
![]()
Also schreiben wir in den Zähler die Ableitung des Arguments der Funktion, und in den Nenner schreiben wir die potentielle Funktion um und multiplizieren sie mit der Quadratwurzel der Funktion des Arguments hoch 2 minus 1: