In diesem Artikel erklären wir, wie man den Kosekans einer Funktion (Formel) ableitet. Außerdem finden Sie Schritt für Schritt gelöste Übungen zur Ableitung des Kosekans. Und schließlich können Sie die Demonstration der Formel für diese Art trigonometrischer Ableitung sehen.
Kosekansableitungsformel
Die Ableitung des Kosekans von x ist gleich minus dem Quotienten aus dem Kosinus von x geteilt durch den Quadratsinus von x.
![]()
Mithilfe trigonometrischer Formeln können wir die Ableitung des Kosekans von x auch als minus dem Produkt aus dem Kotangens von x mal dem Kosekans von x definieren.
![]()
Und wenn wir die Kettenregel anwenden, ist die Ableitung des Kosekans einer Funktion minus dem Produkt aus der Ableitung der Funktion mal dem Kosinus der Funktion geteilt durch den Quadratsinus der Funktion.
![]()
Die Formel zur Ableitung des Kosekans einer Funktion lautet daher wie folgt:
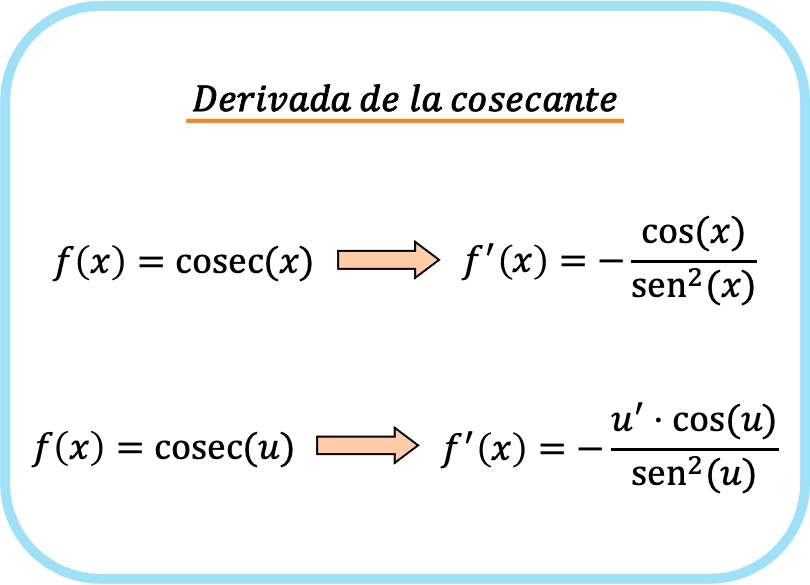
Beispiele für die Ableitung des Kosekans
Nachdem wir gesehen haben, wie die Formel für die Ableitung des Kosekans lautet, geben wir nun einige Beispiele. So können Sie genau sehen, wie der Kosekans einer Funktion abgeleitet wird.
Beispiel 1: Ableitung des Kosekans von 2x
In diesem Beispiel werden wir sehen, wie groß die Ableitung des Kosekans von 2x ist:
![]()
Die Kosekans-Argumentfunktion unterscheidet sich von x, daher müssen wir die Kosekans-Ableitungsregel mit der Kettenregel verwenden.
![]()
Um also die Ableitung dieser trigonometrischen Funktion zu finden, ersetzen Sie einfach die Werte in der vorherigen Formel: In das Kosinus- und Sinus-Argument setzen wir 2x, und u‘ entspricht der Ableitung von 2x, also 2:
![]()
Beispiel 2: Ableitung des Kosekans von x im Quadrat
In dieser Übung werden wir sehen, wie groß die Ableitung des Kosekans von x zum Quadrat ist:
![]()
Logischerweise wird die Ableitung dieser trigonometrischen Funktion mithilfe der Formel für die Ableitung des Kosekans gelöst:
![]()
Die Ableitung von x im Quadrat ergibt 2x, daher ist die Ableitung des Kosekans von x hoch zwei:
![]()
Beispiel 3: Ableitung des dritten Kosekans einer Exponentialfunktion
![]()
Was auch immer das Argument der Funktion ist, die Regel für die Ableitung des Kosekans einer Funktion lautet:
![]()
Aber in diesem Fall haben wir eine zusammengesetzte Funktion, weil der Kosekans auf drei erhöht wird und außerdem in seinem Argument eine Exponentialfunktion vorliegt. Um also die gesamte Funktion zu differenzieren, müssen wir die Kettenregel mehrmals anwenden:
![Rendered by QuickLaTeX.com \begin{aligned}\displaystyle f'(x)& = 3\text{cosec}^2(e^{5x})\cdot\left(-\frac{5e^{5x}\cdot \text{cos}(e^{5x})}{\text{sen}^2(e^{5x})}\right)\\[1.5ex]&=-\frac{-15\text{cosec}^2(e^{5x})\cdot e^{5x}\cdot \text{cos}(e^{5x})}{\text{sen}^2(e^{5x})}\end{aligned}](https://mathority.org/wp-content/ql-cache/quicklatex.com-9ac2ce49dfcba1b7f27696dba0a2decb_l3.png)
Probleme der Ableitung des Kosekans gelöst
Leiten Sie die folgenden Kosekansfunktionen her:
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![Rendered by QuickLaTeX.com \begin{aligned}\text{C) }f'(x)& =-\cfrac{\cfrac{3x^2+14x}{x^3+7x^2}\cdot \text{cos}\bigl(\ln(x^3+7x^2)\bigr)}{\text{sen}^2\bigl(\ln(x^3+7x^2)\bigr)}\\[1.5ex] &= -\cfrac{\cfrac{3x+14}{x^2+7x}\cdot \text{cos}\bigl(\ln(x^3+7x^2)\bigr)}{\text{sen}^2\bigl(\ln(x^3+7x^2)\bigr)}\\[1.5ex] &= -\cfrac{(3x+14)\cdot \text{cos}\bigl(\ln(x^3+7x^2)\bigr)}{(x^2+7x)\cdot \text{sen}^2\bigl(\ln(x^3+7x^2)\bigr)}\end{aligned}](https://mathority.org/wp-content/ql-cache/quicklatex.com-32dde68d2a11ef6a05d483b26f0a98ef_l3.png)
![Rendered by QuickLaTeX.com \begin{aligned}\text{D) }f'(x)& =-\cfrac{-\cfrac{7x^6}{\sqrt{1-\left(x^7\right)^2}}\cdot \text{cos}\bigl(\text{arccos}(x^7)\bigr)}{\text{sen}^2\bigl(\text{arccos}(x^7)\bigr)}\\[1.5ex] & =-\cfrac{(-7x^6)\cdot \text{cos}\bigl(\text{arccos}(x^7)\bigr)}{\left(\sqrt{1-x^{14}}\right)\cdot \text{sen}^2\bigl(\text{arccos}(x^7)\bigr)}\\[1.5ex] & =\cfrac{7x^6\cdot \text{cos}\bigl(\text{arccos}(x^7)\bigr)}{\left(\sqrt{1-x^{14}}\right)\cdot \text{sen}^2\bigl(\text{arccos}(x^7)\bigr)}\end{aligned}](https://mathority.org/wp-content/ql-cache/quicklatex.com-b2bea25dae467cefdcc1bd48e8d9bc88_l3.png)
![Rendered by QuickLaTeX.com \begin{aligned} \text{E) }f'(x)& =-\cfrac{\cfrac{18x-4}{2\cdot\sqrt{9x^2-4x}} \cdot \text{cos}\left(\sqrt{9x^2-4x}\right)}{\text{sen}^2\left(\sqrt{9x^2-4x}\right)}\\[1.5ex] &=-\cfrac{(18x-4)\cdot \text{cos}\left(\sqrt{9x^2-4x}\right)}{2\sqrt{9x^2-4x}\cdot \text{sen}^2\left(\sqrt{9x^2-4x}\right)} \end{aligned}](https://mathority.org/wp-content/ql-cache/quicklatex.com-eb70e1d7b6f2ce2636934b235904861f_l3.png)
Beweis der Formel für die Ableitung des Kosekans
Als nächstes demonstrieren wir die Formel für die Ableitung des Kosekans. Im Gegensatz zu anderen Demonstrationen verwenden wir in diesem Fall nicht den Grenzwert, der eine Ableitung definiert, sondern beginnen mit der mathematischen Definition des Kosekans.
Algebraisch gesehen ist die trigonometrische Kosekansfunktion die multiplikative Umkehrung des Sinus:
![]()
Wir können daher die Ableitung des Kosekans mithilfe der Quotientenregel bilden:
![]()
![]()
Wie Sie sehen, gelangen wir nur durch Anwendung der Regel für die Ableitung einer Division zur Formel für die Ableitung des Kosekans. Und da die Ableitung eines Quotienten bereits bewiesen ist (Sie können sie im folgenden Link sehen), ist auch die Kosekansableitungsregel bewiesen.