Hier erfahren Sie, wie Sie den hyperbolischen Arkustangens einer Funktion ableiten. Sie werden auch gelöste Beispiele dieser Art trigonometrischer Ableitungen sehen können und schließlich zeigen wir Ihnen die Formel für die Ableitung des hyperbolischen Arkustangens.
Formel für die Ableitung des hyperbolischen Arkustangens
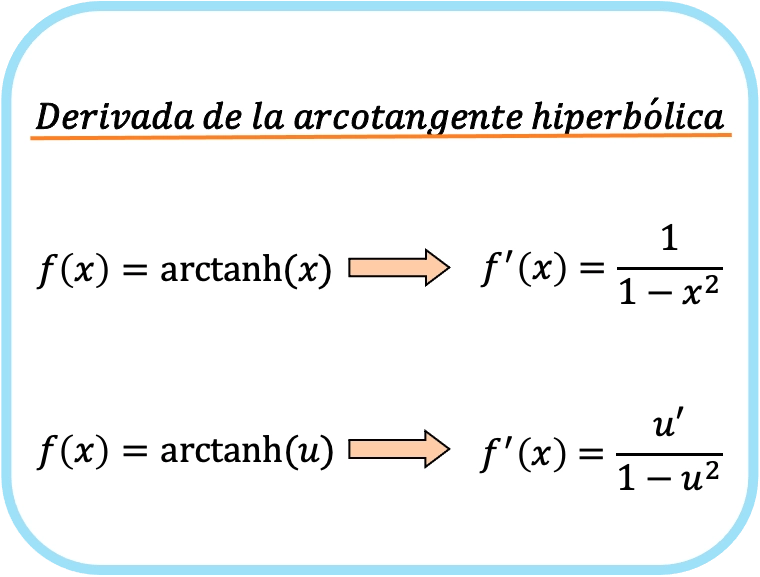
Die Ableitung des hyperbolischen Arkustangens von x ist eins über eins minus x zum Quadrat.
![]()
Daher ist die Ableitung des hyperbolischen Arkustangens einer Funktion gleich dem Quotienten der Ableitung dieser Funktion dividiert durch eins minus dem Quadrat der Funktion.
![]()
Tatsächlich sind beide Formeln gleich, bei der zweiten kommt jedoch die Kettenregel zur Anwendung. Wenn wir beispielsweise x durch u ersetzen, erhalten wir genau die erste Formel, da die Ableitung von x 1 ist.
So wie der Arkustangens die Umkehrfunktion des Tangens ist, ist der hyperbolische Arkustangens die Umkehrfunktion des hyperbolischen Tangens. Obwohl ihre Ableitungen sehr unterschiedlich sind, können Sie die Ableitung dieser trigonometrischen Funktion hier überprüfen:
➤ Siehe: Formel für die Ableitung des Tangens hyperbolicus
Beispiele für die Ableitung des hyperbolischen Arkustangens
Beispiel 1
![]()
Logischerweise müssen wir die Regel der Ableitung des hyperbolischen Arkustangens anwenden:
![]()
Die Ableitung von 2x ist 2, also setzen Sie eine Zwei in den Zähler des Bruchs und eins minus 2x zum Quadrat in den Nenner:
![]()
Beispiel 2
![]()
Um die Ableitung dieser Funktion zu ermitteln, müssen wir die Formel für die Ableitung des hyperbolischen Arkustangens verwenden.
![]()
Darüber hinaus ist die Argumentfunktion des hyperbolischen Arkustangens eine zusammengesetzte Funktion, daher müssen wir auch die Kettenregel anwenden:
![]()
Beweis der Ableitung des hyperbolischen Arkustangens
In diesem letzten Abschnitt werden wir die Formel für die Ableitung des hyperbolischen Arkustangens demonstrieren.
![]()
Da der Arcustangens hyperbolicus der umgekehrte Tangens hyperbolicus ist, können wir die vorherige Gleichheit auf andere Weise ausdrücken:
![]()
Nun unterscheiden wir beide Seiten der Gleichung:
![]()
Wir klären Sie:
![]()
Andererseits wissen wir, dass die Differenz der Quadrate des hyperbolischen Kosinus und des hyperbolischen Sinus 1 ergibt. Wir können daher den vorherigen Ausdruck in einen Bruch umwandeln:
![]()
![]()
Wir dividieren alle Terme des Bruchs durch das Quadrat des hyperbolischen Kosinus:
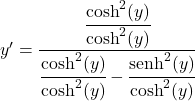
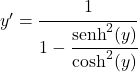
Der Quotient aus dem Sinus hyperbolicus und dem Cosinus hyperbolicus ist gleich dem Tangens hyperbolicus, daher:
![]()
![]()
Aber wie wir zu Beginn des Beweises gesehen haben, ist der Tangens hyperbolicus äquivalent zur Variablen x, daher können wir den Ausdruck ersetzen und so die Formel für die Ableitung des Tangens hyperbolicus erhalten:
![]()