Hier finden Sie die Ableitung des hyperbolischen Arkussinus (Formel). Darüber hinaus können Sie mehrere gelöste Übungen zu den Ableitungen des hyperbolischen Arkussinus einer Funktion sehen. Abschließend zeigen wir Ihnen die Formel für die Ableitung dieser Art trigonometrischer Funktion.
Ableitungsformel des hyperbolischen Arkussinus
Die Ableitung des hyperbolischen Arkussinus von x ist eins über die Quadratwurzel von x zum Quadrat plus 1.
![]()
Die Ableitung des Arkussinus hyperbolicus einer Funktion ist also gleich dem Quotienten der Ableitung dieser Funktion geteilt durch die Quadratwurzel dieser Funktion zum Quadrat plus eins.
![]()
Die zweite Formel ähnelt der ersten, wendet jedoch die Kettenregel an. Das heißt, mit der ersten Formel kann nur der hyperbolische Arkussinus von xy abgeleitet werden, während mit der zweiten Formel der hyperbolische Arkussinus jeder Funktion abgeleitet werden kann.

Bedenken Sie, dass der hyperbolische Arkussinus die Umkehrfunktion des hyperbolischen Sinus ist, dessen Ableitung Sie hier sehen können:
➤ Siehe: Formel für die Ableitung des hyperbolischen Sinus
Beispiele für die hyperbolische Arkussinus-Ableitung
Beispiel 1
![]()
Um die Ableitung der Arkussinusfunktion zu lösen, verwenden wir die oben gezeigte Formel:
![]()
Die Ableitung von 3x ist 3, also steht eine 3 im Zähler. Und in den Nenner müssen wir einfach die Quadratwurzel aus 3x zum Quadrat plus 1 setzen:
![]()
Beispiel 2
![]()
Um den hyperbolischen Arkussinus der Funktion x kubisch abzuleiten, müssen wir dieselbe Formel anwenden:
![]()
Die Ableitung von x quadriert ist 3x 2 , daher ist die Ableitung des hyperbolischen Arkussinus von x erhöht auf 3:
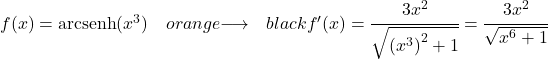
Beweis der hyperbolischen Arkussinus-Ableitung
Wir werden die Formel für die Ableitung des hyperbolischen Arkussinus demonstrieren:
![]()
Zuerst wandeln wir den hyperbolischen Arkussinus in einen hyperbolischen Sinus um:
![]()
Wir folgern aus beiden Seiten der Gleichheit:
![]()
Wir klären Sie:
![]()
Dann wenden wir die trigonometrische Identität an, die den hyperbolischen Sinus und den hyperbolischen Kosinus verbindet:
![]()
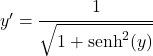
Aber oben haben wir abgeleitet, dass x dem hyperbolischen Sinus von y entspricht, also bleibt die Gleichung bestehen:
![]()
Wie Sie sehen, haben wir durch die Anwendung dieser Schritte die Formel für die Ableitung des hyperbolischen Arkussinus erhalten, weshalb sie bewiesen ist.