Hier erfahren Sie, was die Ableitung des hyperbolischen Tangens einer Funktion ist. Darüber hinaus können Sie mehrere gelöste Beispiele für Ableitungen hyperbolischer Tangenten sehen. Und zum Schluss zeigen wir Ihnen die Formel für die Ableitung des Tangens hyperbolicus.
Formel für die Ableitung des hyperbolischen Tangens
Die Ableitung des Tangens hyperbolicus von x ist gleich 1 dividiert durch das Quadrat des Cosinus hyperbolicus von x. Die Ableitung des Tangens von x entspricht auch dem Quadrat des hyperbolischen Sekanten von x und 1 minus dem Quadrat des hyperbolischen Tangens von x.
![Rendered by QuickLaTeX.com \begin{array}{c}f(x)=\text{tanh}(x)\\[1.5ex]\color{orange}\bm{\downarrow}\color{black}\\ f'(x)=\cfrac{1}{\text{cosh}^2(x)}=\text{sech}^2(x)=1-\text{tanh}^2(x)\end{array}](https://mathority.org/wp-content/ql-cache/quicklatex.com-9a7c392afdb3bbf504e167e15fb2fee6_l3.png)
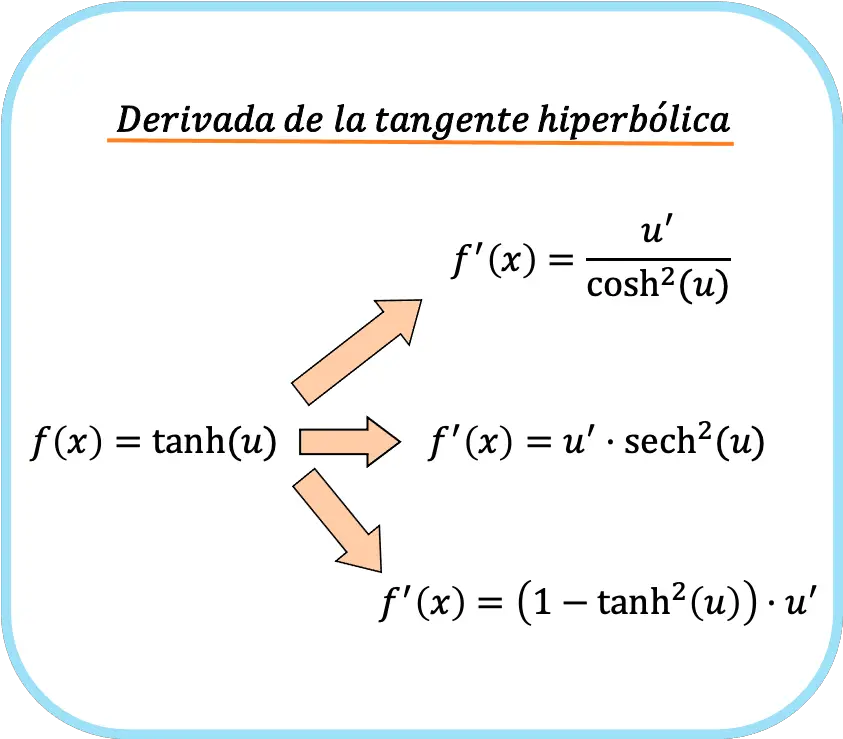
Wenn wir andererseits im Funktionsargument eine andere Funktion als x haben, müssen wir die Kettenregel anwenden. Und dann lauten die drei Formeln für die Ableitung des Tangens hyperbolicus:
![Rendered by QuickLaTeX.com \begin{array}{c}f(x)=\text{tanh}(u)\\[1.5ex]\color{orange}\bm{\downarrow}\color{black}\\ f'(x)=\cfrac{u'}{\text{cosh}^2(u)}=\text{sech}^2(u)\cdot u'=\left(1-\text{tanh}^2(u)\right)\cdot u'\end{array}](https://mathority.org/wp-content/ql-cache/quicklatex.com-b5ee01c6675067b20f71ea8ac4efcfe5_l3.png)
Das bedeutet nicht, dass wir jedes Mal, wenn wir den Tangens hyperbolicus ableiten, alle drei Formeln verwenden müssen, sondern vielmehr, dass wir jede davon verwenden können, um ihn abzuleiten. Abhängig von der Funktion des Tangens-Hyperbolicus-Arguments ist es also besser, die eine oder andere Formel zu verwenden. Nachfolgend finden Sie einige Beispiele, in denen Sie sehen können, wie der hyperbolische Tangens einer Funktion abgeleitet wird.
Die Ableitung des Tangens hyperbolicus ist fast identisch mit der Ableitung des Tangens, weist jedoch ein kleines Detail auf, das sie völlig unterschiedlich macht. Was der Unterschied ist, könnt ihr im folgenden Link sehen:
➤ Siehe:Tangentenableitungsformel
Beispiele für die Ableitung des Tangens hyperbolicus
Nachdem Sie die Formel für die Ableitung des Tangens hyperbolicus gesehen haben, finden Sie hier einige gelöste Beispiele für Ableitungen dieser Art von trigonometrischen Funktionen, damit Sie vollständig verstehen, wie der Tangens hyperbolicus abgeleitet wird.
Beispiel 1: Ableitung des hyperbolischen Tangens von 2x
![]()
Um den Tangens hyperbolicus in diesem Beispiel abzuleiten, verwenden wir die Formel des hyperbolischen Kosinus, obwohl Sie natürlich auch die Formel verwenden können, die Ihnen am besten gefällt.
![]()
Wir wissen, dass die Ableitung von 2x 2 ist, also ist die Ableitung der gesamten Funktion:
![]()
Beispiel 2: Ableitung des hyperbolischen Tangens von x im Quadrat
![]()
Die Regel für die Ableitung des Tangens hyperbolicus einer Funktion lautet:
![]()
Einerseits differenzieren wir die Funktion vom Argument x 2 , was 2x ergibt, und lösen dann die Ableitung der gesamten Funktion mithilfe der Formel auf:
![]()
Beispiel 3: Ableitung des hyperbolischen Tangens kubiert
![]()
In diesem Fall müssen wir den hyperbolischen Tangens einer Funktion ableiten, die noch dazu potenziert wird. Wir müssen also die Formel für die Ableitung einer Potentialfunktion, die Regel für die Ableitung des Tangens hyperbolicus und die Kettenregel verwenden:
![]()
Beweis der Ableitung der Tangente
In diesem Abschnitt zeigen wir die Formel für die Ableitung des Tangens hyperbolicus. Und dazu gehen wir von der trigonometrischen Identität aus, die die drei hyperbolischen trigonometrischen Verhältnisse verbindet:
![]()
➤ Hinweis: Um den Beweis zu verstehen, müssen Sie wissen, was die Ableitung des hyperbolischen Sinus und was die Ableitung des hyperbolischen Kosinus ist. Daher empfehlen wir Ihnen, die verlinkten Seiten zu besuchen, bevor Sie fortfahren.
Wenden wir nun die Formel für die Ableitung eines Quotienten an:
![]()
![]()
![]()
Wir reduzieren den Ausdruck des Zählers des Bruchs mit der folgenden Formel:
![]()
![]()
Wie Sie sehen, entspricht die vorherige Gleichung der ersten Formel für die Ableitung des Tangens hyperbolicus. Ebenso ist die hyperbolische Sekante die multiplikative Umkehrung des hyperbolischen Kosinus, daher wird auch die zweite Formel abgeleitet:
![]()
Schließlich können wir zur dritten Regel der Ableitung des Tangens hyperbolicus gelangen, indem wir den Bruch aus dem vorherigen Schritt in eine Subtraktion von Brüchen umwandeln:
![]()
![]()
![]()