Ableitung des Arkuskosinus

Hier erklären wir, wie man den Arkuskosinus einer Funktion ableitet. Darüber hinaus finden Sie Beispiele für Ableitungen des Arkuskosinus und können mit Schritt für Schritt gelösten Übungen üben. Abschließend zeigen wir Ihnen den Beweis der Arkuskosinus-Ableitungsformel.

Was ist die Ableitung des Arkuskosinus?

Die Ableitung des Arkuskosinus von x ist negativ eins über der Quadratwurzel von eins minus x im Quadrat.

$f(x)=\text{arccos}(x) \quad\color{orange}\bm{\longrightarrow}\quad\color{black} f'(x)=-\cfrac{1}{\sqrt{1-x^2}}$

Daher ist die Ableitung des Arkuskosinus einer Funktion gleich minus dem Quotienten der Ableitung dieser Funktion geteilt durch die Quadratwurzel von eins minus dem Quadrat dieser Funktion.

$f(x)=\text{arccos}(u) \quad\color{orange}\bm{\longrightarrow}\quad\color{black} f'(x)=-\cfrac{u'}{\sqrt{1-u^2}}$

Tatsächlich erhält man die erste Formel, indem man in der zweiten Formel x durch u ersetzt. Um es noch einmal zusammenzufassen: Die Formel für die Ableitung des Umkehrkosinus lautet:

Wie Sie sehen können, ähnelt die Formel für die Ableitung des Arkuskosinus der Ableitung des Arkussinus , fügt jedoch davor ein Negativ hinzu.

Beispiele für die Arcus-Cosinus-Ableitung

Angesichts der Formel für die Ableitung der Arkuskosinusfunktion werden wir nun mehrere Beispiele dieser Art trigonometrischer Ableitungen analysieren. Auf diese Weise können Sie leichter verstehen, wie der Arkuskosinus einer Funktion abgeleitet wird.

Beispiel 1: Ableitung des Arcuscosinus von 2x

$f(x)=\text{arccos}(2x)$

Um die Ableitung des Arkuskosinus zu lösen, verwenden wir seine Formel:

$f(x)=\text{arccos}(u) \quad\color{orange}\bm{\longrightarrow}\quad\color{black} f'(x)=-\cfrac{u'}{\sqrt{1-u^2}}$

Die Ableitung von 2x ist 2, also ist die Arcuskosinus-Ableitung von 2x negativ 2 über der Wurzel eins minus 2x im Quadrat:

$f(x)=\text{arccos}(2x) \quad\color{orange}\bm{\longrightarrow}\quad\color{black} f'(x)=-\cfrac{2}{\sqrt{1-(2x)^2}}=-\cfrac{2}{\sqrt{1-4x^2}}$

Beispiel 2: Ableitung des Arcuskosinus von x im Quadrat

$f(x)=\text{arccos}(x^2)$

Wir wenden die Arkuskosinus-Ableitungsformel mit der Kettenregel an, um die Ableitung zu berechnen:

$f(x)=\text{arccos}(u) \quad\color{orange}\bm{\longrightarrow}\quad\color{black} f'(x)=-\cfrac{u'}{\sqrt{1-u^2}}$

Da die Ableitung der Funktion x ² 2x ist, ist die Ableitung des Arkuskosinus von x hoch 2:

$f(x)=\text{arccos}(x^2) \quad\color{orange}\bm{\longrightarrow}\quad\color{black} f'(x)=-\cfrac{2x}{\sqrt{1-\left(x^2\right)^2}}=-\cfrac{2x}{\sqrt{1-x^4}}$

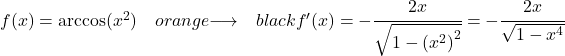
Beispiel 3: Ableitung des Arkuskosinus eines Logarithmus

$f(x)=\text{arccos}\bigl(\ln (x)\bigr)$

Die Funktion in diesem Beispiel besteht aus einem Arkuskosinus und einem natürlichen Logarithmus, daher müssen wir die Kettenregel verwenden, um sie abzuleiten.

$f(x)=\text{arccos}(u) \quad\color{orange}\bm{\longrightarrow}\quad\color{black} f'(x)=-\cfrac{u'}{\sqrt{1-u^2}}$

Die Ableitung des natürlichen Logarithmus ist eins dividiert durch x, daher ist die Ableitung der ganzzahligen Funktion:

$f(x)=\text{arccos}\bigl(\ln (x)\bigr) \quad\color{orange}\bm{\longrightarrow}\quad\color{black} f'(x)=-\cfrac{\cfrac{1}{x}}{\sqrt{1-\left(\ln(x)\right)^2}}=\cfrac{1}{x\sqrt{1-\ln^2(x)}}$

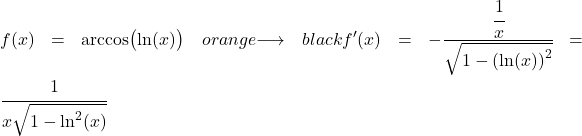
Die Arkuskosinus-Ableitung löste Probleme

Leiten Sie die folgenden Arkuskosinusfunktionen ab:

$\text{A) }f(x)=\text{arccos}(7x)$

$\text{B) }f(x)=\text{arccos}(x^3+6x)$

$\text{C) }f(x)=\text{arccos}^3\left(e^{3x}\right)$

$\text{D) }f(x)=\text{arccos}\left(\log_3(x^3)\right)$

$\text{E) }f(x)=\text{arccos}\left(\sqrt{4x}\right)$

siehe Lösung

$\text{A) }f'(x)=-\cfrac{7}{\sqrt{1-(7x)^2}}=-\cfrac{7}{\sqrt{1-49x^2}}$

$\text{B) }f'(x)=-\cfrac{3x^2+6}{\sqrt{1-(x^3+6x)^2}}$

$\begin{aligned}\text{C) }\displaystyle f'(x)&=3\text{arccos}^2\left(e^{3x}\right)\cdot \left(-\frac{3e^{3x}}{\sqrt{1-\left(e^{3x}\right)^2}}\right)\\[1.5ex] &=-\cfrac{9\text{arccos}^2\left(e^{3x}\right)\cdot e^{3x}}{\sqrt{1-e^{6x}}}\end{aligned}$

$\begin{aligned}\text{D) }f'(x)&=-\cfrac{1}{\sqrt{1-\left(\log_3(3x)\right)^2}}\cdot \cfrac{3}{3x\cdot \ln 3}\\[1.5ex] &=-\cfrac{1}{x\cdot \ln 3\cdot \sqrt{1-\log_3^2(3x)}} \end{aligned}$

$\begin{aligned}\text{E) } f'(x)& =-\cfrac{1}{\sqrt{1-\left(\sqrt{4x}\right)^2}}\cdot \cfrac{4}{2\sqrt{4x}}\\[1.5ex] &=-\cfrac{2}{\sqrt{1-4x}\cdot 2\sqrt{x}}\\[1.5ex] &=-\cfrac{1}{\sqrt{x-4x^2}} \end{aligned}$