In diesem Artikel erklären wir, wie man den Arkussinus einer Funktion ableitet. Sie finden Beispiele für Ableitungen des Arkussinus von Funktionen und können sogar mit Schritt für Schritt gelösten Übungen üben. Schließlich sehen Sie auch die Demonstration der Arkussinus-Ableitungsformel.
Was ist die Ableitung des Arkussinus?
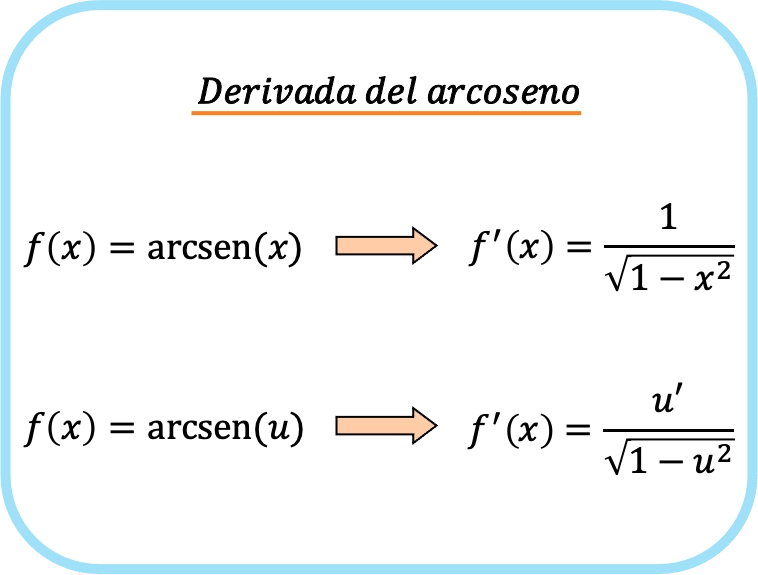
Die Arkussinusableitung von x ist eins über der Quadratwurzel von eins minus x im Quadrat.
![]()
Daher ist die Ableitung des Arkussinus einer Funktion gleich dem Quotienten aus der Ableitung dieser Funktion dividiert durch die Quadratwurzel aus eins minus der quadrierten Funktion.
![]()
Logischerweise erhält man die zweite Formel durch Anwendung der Kettenregel auf die erste Formel.
Denken Sie daran, dass der Arkussinus die Umkehrfunktion des Sinus ist, weshalb er auch Umkehrsinus genannt wird.
Beispiele für Arkussinusableitungen
Nachdem wir die Formel für die Arkussinus-Ableitung kennengelernt haben, erklären wir einige Beispiele dieser Art trigonometrischer Ableitungen. Auf diese Weise können Sie leichter verstehen, wie der Arkussinus einer Funktion abgeleitet wird.
Beispiel 1: Ableitung des Arkussinus von 2x
![]()
Um die Ableitung der Arkussinusfunktion zu finden, müssen wir die entsprechende Formel verwenden:
![]()
Die Ableitung von 2x ist also 2, also ist die Arkussinus-Ableitung von 2x 2 dividiert durch die Wurzel aus eins minus 2x im Quadrat:
![]()
Beispiel 2: Ableitung des Arkussinus von x im Quadrat
![]()
Zur Ableitung verwenden wir die Arkussinus-Ableitungsformel:
![]()
Die Funktion x 2 ist zweiten Grades, daher ist ihre Ableitung 2x. Somit ist die Ableitung des Arkussinus von x hoch 2:
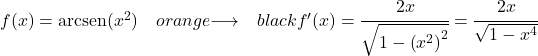
Beispiel 3: Ableitung des Arkussinus von e x
![]()
Die Funktion in diesem Beispiel ist eine zusammengesetzte Funktion, daher müssen wir die Kettenregel anwenden, um die Ableitung zu lösen:
![]()
Die Ableitung von e x ist sie selbst, also ist die Ableitung der gesamten Funktion:
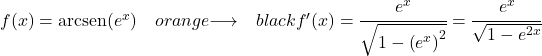
Probleme mit der Arcussinus-Ableitung gelöst
Leiten Sie die folgenden Arkussinusfunktionen ab:
![]()
![]()
![]()
![]()
![]()
![]()
![]()
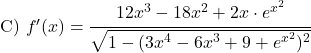
![Rendered by QuickLaTeX.com \begin{aligned}\text{E) } f'(x)& =\cfrac{1}{\sqrt{1-\left(\sqrt{4x}\right)^2}}\cdot \cfrac{4}{2\sqrt{4x}}\\[1.5ex] &=\cfrac{2}{\sqrt{1-4x}\cdot 2\sqrt{x}}\\[1.5ex] &=\cfrac{1}{\sqrt{x-4x^2}} \end{aligned}](https://mathority.org/wp-content/ql-cache/quicklatex.com-0a82c0fd18a8672100ed3b79525a1028_l3.png)
Beweis der Arkussinus-Ableitungsformel
Als nächstes fahren wir mit dem mathematischen Beweis der Formel für die Ableitung des Arkussinus fort.
![]()
Zuerst wandeln wir den Arkussinus in einen Sinus um:
![]()
Nun unterscheiden wir beide Seiten der Gleichung:
![]()
Wir klären Sie:
![]()
Als nächstes wenden wir die grundlegende trigonometrische Identität an:
![]()
![]()
Und da wir oben abgeleitet haben, dass x dem Sinus von y entspricht, bleibt die Gleichheit bestehen:
![]()
Wie Sie sehen können, haben wir durch die Anwendung dieses Verfahrens die Formel für die Ableitung der Arkussinusfunktion erhalten, es ist also gezeigt, dass die Formel erfüllt ist.