Hier erklären wir, wie man die Ableitung einer Wurzel (oder einer Wurzelfunktion) bildet. Sie finden die Formel zur Division von Wurzeln und Schritt für Schritt gelöste Übungen für Ableitungen von Wurzeln.
Formel für die Ableitung einer Wurzel
Die Ableitung einer Wurzel oder irrationalen Funktion ist gleich der Ableitung des Radikanden (Ausdruck unter der Wurzel), dividiert durch das Produkt aus dem Index der Wurzel und derselben Wurzel, wobei 1 vom Exponenten des Radikanden abgezogen wird.
![]()
Wenn der Wurzelradikand jedoch nur ein x ist, vereinfachen sich die Formeln. Die Wurzelableitung von x ist daher die folgende:
![]()
Kurz gesagt, es gibt zwei Formeln zum Ableiten einer Wurzel: die erste, die immer verwendet werden kann, und die zweite, die nur verwendet werden kann, wenn der Radikand x ist.
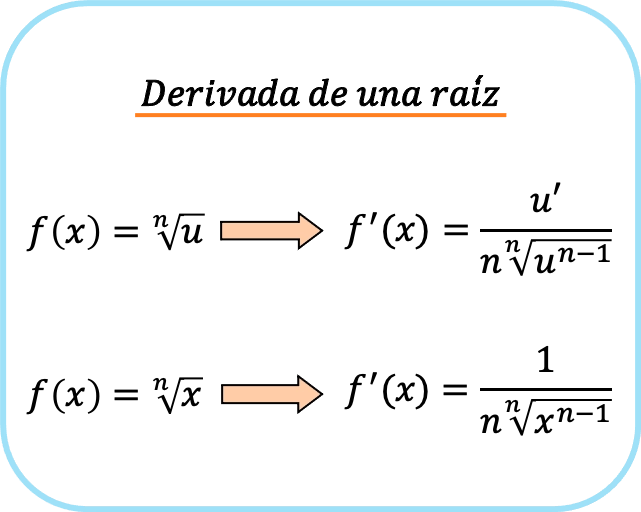
Wenn Sie genau hinschauen, ist der Term im Zähler des Bruchs derjenige, der sich aus der Anwendung der Kettenregel bei der Ableitung der Wurzel ergibt. Aus diesem Grund erscheint 1 im Nenner, wenn der Radikand x ist, da es sich um die Ableitung von x handelt.
Beispiele für Wurzelableitungen
Anhand der Formel für die Ableitung einer Wurzelfunktion erklären wir im Folgenden einige Beispiele dieser Art von Ableitung, damit Sie verstehen, wie man die Ableitung einer Wurzel bildet.
Beispiel 1: Ableitung einer Quadratwurzel
Wir werden dann sehen, was die Ableitung einer Quadratwurzel ist:
![]()
In diesem Fall ist der Ausdruck innerhalb der Wurzel nur ein x, sodass wir die folgende Formel verwenden können:
![]()
Die Ableitung einer Quadratwurzel ist also gleich 1 dividiert durch das Produkt aus 2 mal der Quadratwurzel von x:
![]()
Beispiel 2: Ableitung einer Kubikwurzel
![]()
In diesem Beispiel ist der Ausdruck unter der Wurzel ein x, sodass wir die folgende Formel anwenden können:
![]()
Die Ableitung einer Kubikwurzel ist also gleich 1 dividiert durch das Dreifache der Kubikwurzel von x zum Quadrat:
![]()
Beispiel 3: Ableitung einer vierten Wurzel
![]()
Jetzt haben wir kein x unter dem Wurzelzeichen, aber wir haben einen komplexeren algebraischen Ausdruck. Daher müssen wir die allgemeine Formel für die Ableitung einer Wurzel verwenden:
![]()
Der Ausdruck unter der Wurzel ist eine Funktion ersten Grades, daher ist ihre Ableitung 7. Somit ist die Ableitung der gesamten Funktion:
![]()
Beispiel 4: Ableitung von einer Wurzel zur anderen
![]()
Um die Ableitung dieser aus einer anderen Wurzel zusammengesetzten Wurzel zu lösen, müssen wir die folgende Formel anwenden:
![]()
In diesem Fall müssen Sie dieselbe Formel zweimal hintereinander verwenden, um die Ableitung zu berechnen:
![Rendered by QuickLaTeX.com \begin{aligned}f'(x)& =\cfrac{1}{2\sqrt{x^2+\sqrt[3]{x^4-5}}}\cdot\left(x^2+\sqrt[3]{x^4-5}\right)' \\[3ex]&\displaystyle =\cfrac{1}{2\sqrt{x^2+\sqrt[3]{x^4-5}}}\cdot \left(2x+\frac{1}{ 3\sqrt[3]{(x^4-5)^2}}\cdot (x^4-5)'\right)\\[3ex]&\displaystyle =\cfrac{1}{2\sqrt{x^2+\sqrt[3]{x^4-5}}}\cdot \left(2x+\frac{1}{ 3\sqrt[3]{(x^4-5)^2}}\cdot 4x^3\right)\end{aligned}](https://mathority.org/wp-content/ql-cache/quicklatex.com-c37131b50bda38022296c6401af727ce_l3.png)
Probleme der Ableitung einer Wurzel gelöst
Berechnen Sie die Ableitungen der folgenden Wurzeln:
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![Rendered by QuickLaTeX.com \text{B) } f'(x)=\cfrac{4x^3}{3\sqrt[3]{\left(x^4\right)^2}}= \cfrac{4x^3}{3\sqrt[3]{x^8}}](https://mathority.org/wp-content/ql-cache/quicklatex.com-3bacf51d3e3fd8fa192f982456f2a8d6_l3.png)
![]()
![Rendered by QuickLaTeX.com \text{D) } f'(x)=\cfrac{9x^8+20x^3-2}{4\sqrt[4]{\left(x^9+5x^4-2x\right)^3}}](https://mathority.org/wp-content/ql-cache/quicklatex.com-5169c93bdfa2522a3219563eee1bb354_l3.png)
![Rendered by QuickLaTeX.com \text{E) } f'(x)=\cfrac{3\cdot 4 \cdot (x^2-1)^3\cdot 2x}{5\sqrt[5]{\left(3\left(x^2-1\right)^4\right)^4}}=\cfrac{24x(x^2-1)^3}{5\sqrt[5]{81\left(x^2-1\right)^{16}}}](https://mathority.org/wp-content/ql-cache/quicklatex.com-f68dce6e62d98d10d99daf57e0128069_l3.png)
![Rendered by QuickLaTeX.com \text{F) } f'(x)=\cfrac{2x+2\cdot 4(5x^3-8x)\cdot (15x^2-8)}{6\sqrt[6]{\left(x^2+4(5x^3-8x)^2\right)^5}}=\cfrac{2x+8(5x^3-8x)(15x^2-8)}{6\sqrt[6]{\left(x^2+4(5x^3-8x)^2\right)^5}}](https://mathority.org/wp-content/ql-cache/quicklatex.com-dd1d3bbced66caaed0ac254363e5f2f1_l3.png)