Ableitung einer linearen Funktion

In diesem Artikel zeigen wir Ihnen, wie groß die Ableitung einer linearen Funktion ist. Darüber hinaus lösen wir mehrere Beispiele für Ableitungen linearer Funktionen und demonstrieren die Formel für diese Art von Ableitung. Sie finden dort sogar gelöste Übungen zu den Ableitungen linearer Funktionen.

Was ist die Ableitung einer linearen Funktion?

Die Ableitung einer linearen Funktion ist der Koeffizient des ersten Grades , das heißt, die Ableitung einer linearen Funktion f(x)=Ax+B ist gleich A.

$f(x)=Ax+B\quad\color{orange}\bm{\longrightarrow}\color{black}\quad f'(x)=A$

Der unabhängige Term wird aus der Ableitung entfernt, da die Ableitung einer Konstante Null ist. Und andererseits ist die Ableitung eines Termes ersten Grades der Koeffizient dieses Termes. Daher ist die Ableitung der Summe dieser beiden Arten von Funktionen der Koeffizient des linearen Termes.

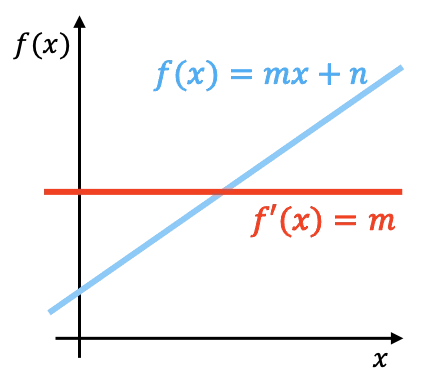
Geometrisch gesehen ist die Ableitung einer linearen Funktion die Steigung dieser Funktion. In der obigen Grafik sehen Sie eine lineare Funktion mit ihrer Ableitung dargestellt.

Beispiele für Ableitungen linearer Funktionen

Angesichts der Definition der Ableitung einer linearen Funktion berechnen wir mehrere Beispiele linearer Funktionen, um das Konzept vollständig zu verstehen:

$\begin{array}{c}f(x)=3x+1\quad\longrightarrow\quad f'(x)=3\\[3ex]f(x)=5x-4\quad\longrightarrow\quad f'(x)=5\\[3ex] f(x)=-2x+9\quad\longrightarrow\quad f'(x)=-2\end{array}$

Beachten Sie, dass die Ableitung der linearen Funktion immer die Zahl ist, die die Variable x begleitet, wenn die Funktion keinen unabhängigen Term hat, oder mit anderen Worten, wenn sie nur einen Term ersten Grades hat. Zum Beispiel:

$f(x)=8x\quad\longrightarrow\quad f'(x)=8$

Daher ist die Ableitung einer linearen Funktion eine Funktion ohne unabhängige Variable, eine einfache Zahl.

Beweis der Ableitung einer linearen Funktion

Als nächstes demonstrieren wir die Formel für die Ableitung einer linearen Funktion.

Sei f eine beliebige lineare Funktion:

$f(x)=Ax+B$

Die Formel zur Berechnung der Ableitung einer Funktion an einem Punkt lautet:

$\displaystyle f'(a)=\lim_{h\to 0}\frac{f(a+h)-f(a)}{h}$

Wenn wir also den vorherigen Grenzwert für eine lineare Funktion berechnen, erhalten wir:

$\displaystyle f'(a)=\lim_{h\to 0}\frac{f(a+h)-f(a)}{h}=\frac{A(a+h)+B-(A\cdot a+B)}{h}$

Wir lösen die Klammern auf:

$\displaystyle f'(a)=\frac{Aa+Ah+B-Aa-B}{h}$

Wir operieren im Zähler:

$\displaystyle f'(a)=\frac{Ah}{h}$

Und schließlich vereinfachen wir den Bruch:

$\displaystyle f'(a)=A$

Zusammenfassend lässt sich sagen, dass die Ableitung einer linearen Funktion an jedem Punkt gleich dem Koeffizienten des Termes ersten Grades ist. Somit wird die Formel für die Ableitung einer linearen Funktion abgeleitet.

Probleme der Ableitungen linearer Funktionen gelöst

Berechnen Sie die Ableitungen der folgenden linearen Funktionen:

$\text{A)}\ f(x)=2x-25$

$\text{B)}\ f(x)=x+3$

$\text{C)}\ f(x)=-9x-1$

$\text{D)}\ f(x)=\cfrac{1}{2}x+7$

$\text{E)}\ f(x)=5x$

$\text{F)}\ f(x)=\sqrt{7}x+\frac{3}{4}$

siehe Lösung

Um eine lineare Funktion abzuleiten, eliminieren Sie einfach den konstanten Term und die Variable aus der Funktion, sodass nur der Koeffizient des linearen Termes übrig bleibt. Noch:

$\text{A)}\ f'(x)=2$