Unendliche unbestimmtheit zwischen unendlichkeit (∞/∞)

In diesem Artikel erklären wir, wie man die Unendlichkeit der Unbestimmtheit zwischen Unendlichkeit (∞/∞) berechnet. Beispiele für diese Unbestimmtheit finden Sie bei allen Arten von Funktionen: Polynom-, Wurzel-, Exponentialfunktionen usw. Darüber hinaus können Sie mit Schritt für Schritt gelösten Übungen zu Grenzwerten trainieren, die unendliche Unbestimmtheiten zwischen Unendlichkeiten ergeben.

So lösen Sie die unendliche Unbestimmtheit zwischen unendlich

Wenn der Grenzwert einer Funktion Unendlich geteilt durch Unendlich ergibt, bedeutet dies, dass es sich um eine Unbestimmtheit (oder unbestimmte Form) handelt. Um den Grenzwert einer Funktion zu lösen, die eine Unendlichkeit der Unbestimmtheit zwischen Unendlichkeiten ergibt, muss der Grad des Zählerpolynoms mit dem Grad des Nennerpolynoms verglichen werden.

\displaystyle\lim_{x\to +\infty}\frac{a_nx^r+a_{n-1}x^{r-1}+a_{n-2}x^{r-2}+\dots}{b_nx^s+b_{n-1}x^{s-1}+b_{n-2}x^{s-2}+\dots}=\frac{+\infty}{+\infty}

Das Ergebnis der Unbestimmtheit Unendlichkeit geteilt durch Unendlich hängt vom Grad des Zählers und vom Grad des Nenners des Bruchs ab:

  1. Wenn der Grad des Zählerpolynoms kleiner ist als der Grad des Nennerpolynoms, ist die Unendlichkeit der Unbestimmtheit geteilt durch Unendlich gleich Null.
  2. Wenn der Grad des Zählerpolynoms dem Grad des Nennerpolynoms entspricht, ist die unendliche Unbestimmtheit über Unendlich der Quotient der führenden Koeffizienten der beiden Polynome.
  3. Wenn der Grad des Zählerpolynoms größer ist als der Grad des Nennerpolynoms, ergibt die Unendlichkeit der Unbestimmtheit zwischen Unendlichkeit mehr oder weniger Unendlichkeit (das Vorzeichen hängt von den Haupttermen der beiden Polynome ab).

\displaystyle \lim_{x \to \pm \infty}}\frac{a_nx^r+a_{n-1}x^{r-1}+a_{n-2}x^{r-2}+\dots}{b_nx^s+b_{n-1}x^{s-1}+b_{n-2}x^{s-2}+\dots}=\left\{ \begin{array}{lcl} 0 & \text{si} & r<s \\[3ex]="" \cfrac{a_n}{b_n}="" &="" \text{si}="" r="s" \\[5ex]="" \pm="" \infty="">s \end{array}\right.“ title=“Rendered by QuickLaTeX.com“ height=“139″ width=“767″ style=“vertical-align: 0px;“></p> </p> <h2 class= Beispiele für unendliche Unbestimmtheiten zwischen Unendlichkeit

Sehen wir uns an, wie die unbestimmte Form Unendlichkeit zwischen Unendlichkeit gelöst wird, indem wir uns für jeden Fall mehrere Beispiele ansehen:

Grad des Zählers kleiner als der Grad des Nenners

Wie wir oben gesehen haben, ergibt die unendliche unbestimmte Grenze zwischen Unendlichkeit immer 0, wenn der Grad des Zählerpolynoms kleiner als der Grad des Nennerpolynoms ist.

Beispiel 1:

\displaystyle \lim_{x \to +\infty} \cfrac{6x^2-5}{x^3+1} = \cfrac{6(+\infty)^2}{(+\infty)^3} = \cfrac{+\infty}{+\infty}= \bm{0}

Das Polynom des Zählers ist vom zweiten Grad, das des Nenners vom dritten Grad, sodass die Lösung des Grenzwerts 0 ist.

Beispiel 2:

\displaystyle \lim_{x \to -\infty} \frac{-7x}{2x^4+3x^2}=\frac{-7\cdot (-\infty)}{2(-\infty)^4}=\frac{+\infty}{+\infty}= \bm{0}

Die Polynomfunktion des Zählers ist vom ersten Grad, aber die Funktion des Nenners ist vom vierten Grad, sodass die Grenze zur negativen Unendlichkeit 0 ist.

Grad des Zählers gleich dem Grad des Nenners

Wenn der Grad des Zählerpolynoms gleich dem Grad des Nennerpolynoms ist, wird der unbestimmte Grenzwert Unendlich durch Unendlich berechnet, indem die führenden Koeffizienten (Koeffizient des Termes höheren Grades) der beiden Polynome dividiert werden.

Beispiel 3:

\displaystyle \lim_{x \to +\infty} \cfrac{4x^2+1}{2x^2-5} = \cfrac{4(+\infty)^2}{2(+\infty)^2}= \cfrac{+\infty}{+\infty} =\cfrac{4}{2} = \bm{2}

In diesem Fall sind die beiden Polynome zweiten Grades, daher ist es notwendig, die Koeffizienten der Terme höheren Grades zu dividieren, um den Grenzwert im positiven Unendlichen zu finden.

Beispiel 4:

\displaystyle \lim_{x \to -\infty} \cfrac{2x+1}{5x+3} = \cfrac{2(-\infty)}{5(-\infty)}= \cfrac{-\infty}{-\infty} =\cfrac{\bm{2}}{\bm{5}}

Obwohl die Grenze liegt, wenn x gegen minus Unendlich tendiert, löst sich die unendliche Unbestimmtheit zwischen Unendlichkeit auf die gleiche Weise auf.

Grad des Zählers größer als der Grad des Nenners

Wenn der Grad des Zählerpolynoms größer ist als der Grad des Nennerpolynoms, ergibt die unbestimmte Form der Unendlichkeit zwischen Unendlichkeit immer Unendlichkeit, und das Vorzeichen der Unendlichkeit wird durch die Terme höherer Ordnung der beiden Polynome bestimmt.

Beispiel 5:

\displaystyle \lim_{x \to +\infty} \cfrac{x^2+7}{x-2} = \cfrac{(+\infty)^2}{+\infty} = \cfrac{+\infty}{+\infty} = \bm{+\infty}

Die Funktion des Zählers hat einen höheren Grad als die des Nenners, daher ergibt die Unbestimmtheit Unendlich über Unendlich Unendlich. Außerdem erhalten in diesem Fall sowohl der Zähler als auch der Nenner eine positive Unendlichkeit, sodass das Ergebnis des Grenzwerts ebenfalls positiv sein muss.

Beispiel 6:

\displaystyle \lim_{x \to -\infty} \cfrac{3x^2+2x-5}{7x+1} = \cfrac{3(-\infty)^2}{7(-\infty)}=\cfrac{3(+\infty)}{-\infty}}= \cfrac{+\infty}{-\infty}= \bm{-\infty}

Bei diesem Problem ergibt sich aus dem Zähler eine positive Unendlichkeit, da jeder quadrierte Term positiv ist. Andererseits ergibt sich aus dem Nenner eine negative Unendlichkeit. Daher ist der resultierende Grenzwert negativ, da das Positive geteilt durch das Negative gleich dem Negativen ist.

Unendliche Unbestimmtheit zwischen Unendlichkeit und Wurzeln

Wir haben gerade gesehen, wie man die unendliche Unbestimmtheit zwischen Unendlichkeit berechnet, wenn wir Polynomfunktionen haben. Aber… wie viel ist Unendlich durch Unendlich geteilt, wenn wir Wurzeln haben?

Der Grad einer irrationalen Funktion (Funktion mit Wurzeln) ist der Quotient zwischen dem Grad des Hauptterms und dem Index der Wurzel.

\sqrt[\color{red}\bm{m}\color{black}]{a_nx^{\color{blue}\bm{n}\color{black}}+a_{n-1}x^{n-1}+a_{n-2}x^{n-2}+\dots} \ \longrightarrow \ \text{grado}=\cfrac{\color{blue}\bm{n}\color{black}}{\color{red}\bm{m}\color{black}}

Wenn also der Grenzwert einer Funktion mit Wurzeln die Unbestimmtheit zwischen Unendlichkeit angibt , müssen wir dieselben oben erläuterten Regeln für die Grade des Zählers und des Nenners anwenden, wobei jedoch zu berücksichtigen ist, dass der Grad eines Polynoms mit Wurzeln unterschiedlich berechnet wird.

Schauen Sie sich das folgende Beispiel für den Grenzwert einer Funktion mit Radikalen ins Unendliche an:

\displaystyle\lim_{x\to +\infty}\frac{4x^2+11}{\sqrt{x^8-3x^2-5}}=\frac{4(+\infty)^2}{\sqrt{(+\infty)^8}}=\frac{+\infty}{+\infty}=\bm{0}

Der Grad des Zählers ist 2 und der Grad des Nenners ist 4 (8/2=4), daher ist die Grenze 0, da der Grad des Zählers kleiner als der Grad des Nenners ist.

Wenn andererseits der Grad des Zählers und des Nenners gleich sind, müssen wir zur Berechnung des unbestimmten Grenzwerts den Hauptkoeffizienten mit der Wurzel nehmen:

\displaystyle\lim_{x\to +\infty}\frac{6x-5}{\sqrt{9x^2+2x}}=\frac{6(+\infty)}{\sqrt{9(+\infty)^2}}=\frac{+\infty}{+\infty}=\frac{6}{\sqrt{9}}=\frac{6}{3}=\bm{2}

Unendliche Unbestimmtheit zwischen Unendlichkeit und Exponentialfunktionen

Schließlich müssen wir nur noch einen Fall des Unbestimmtheitsquotienten von Unendlichkeiten untersuchen: Wie groß ist die unendliche Unbestimmtheit zwischen Unendlichkeit und Exponentialfunktionen?

Das Wachstum einer Exponentialfunktion ist viel größer als das Wachstum einer Polynomfunktion, daher müssen wir berücksichtigen, dass der Grad einer Exponentialfunktion größer ist als der Grad einer Polynomfunktion.

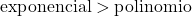
\text{exponencial}>\text{polinomio}“ title=“Rendered by QuickLaTeX.com“ height=“16″ width=“192″ style=“vertical-align: -4px;“></p> </p> <p> Wenn sich also aus einem Grenzwert mit Exponentialfunktionen eine unendliche Unbestimmtheit dividiert durch Unendlich ergibt, reicht es aus, die gleichen Regeln anzuwenden, die für die Grade des Zählers und des Nenners erläutert wurden, wobei jedoch zu berücksichtigen ist, dass eine Exponentialfunktion von höherer Ordnung als ein Polynom ist. .</p> <p> Wenn wir außerdem Exponentialfunktionen im Zähler und Nenner der Division haben, ist die Exponentialfunktion mit der größeren Basis von höherer Ordnung.</p> </p> <p class=\displaystyle\lim_{x\to +\infty}\frac{7x^5+6x^3-4x}{4^x}=\frac{7(+\infty)^5}{4^{+\infty}}=\frac{+\infty}{+\infty}=\bm{0}

In diesem Fall wird der Nenner durch eine Exponentialfunktion gebildet, ist also von höherer Ordnung als der Zähler. Daher verschwindet die unbestimmte Form Unendlichkeit zwischen Unendlichkeit.

Gelöste Übungen zur unendlichen Unbestimmtheit zwischen Unendlichkeit

Übung 1

Berechnen Sie den Grenzwert der folgenden rationalen Funktion:

\displaystyle\lim_{x \to +\infty} \cfrac{6x-5}{x^2-1}

Bei der Berechnung der Grenze erhalten wir die unendliche Unbestimmtheit zwischen Unendlichkeit, aber da der Grad des Zählers kleiner ist als der Grad des Nenners, ist die unbestimmte Grenze gleich Null.

\displaystyle \lim_{x \to +\infty} \cfrac{6x-5}{x^2-1} = \cfrac{6(+\infty)}{(+\infty)^2} = \cfrac{+\infty}{+\infty}= \bm{0}

Übung 2

Lösen Sie den folgenden unbestimmten Grenzwert:

\displaystyle\lim_{x \to +\infty} \cfrac{x^3+4x-1}{5x^2-3x+4}

Beim Versuch, den Grenzwert zu berechnen, erhält man die Unbestimmtheit ∞/∞. In diesem Fall ist der Grad des Zählerpolynoms größer als der Grad des Nennerpolynoms, sodass der unbestimmte Grenzwert gleich plus Unendlich ist.

\displaystyle \lim_{x \to +\infty} \cfrac{x^3+4x-1}{5x^2-3x+4} = \cfrac{(+\infty)^3}{5(+\infty)^2} = \cfrac{+\infty}{+\infty}= \bm{+\infty}

Übung 3

Lösen Sie den folgenden Grenzwert im Unendlichen:

\displaystyle \lim_{x \to +\infty} \cfrac{-4x^2+3}{3x+1}

Der Grenzwert ergibt Unbestimmtheit minus Unendlichkeit zwischen plus Unendlichkeit. Der Grad des Zählers ist größer als der Grad des Nenners, daher ist die unbestimmte Grenze gleich plus Unendlich. Da die Division jedoch negativ Unendlich durch positiv Unendlich ist, ist das Ergebnis minus Unendlich.

\displaystyle \lim_{x \to +\infty} \cfrac{-4x^2+3}{3x+1} = \cfrac{-4(+\infty)^2}{3(+\infty)} =\cfrac{-4(+\infty)}{+\infty}= \cfrac{-\infty}{+\infty}= \bm{-\infty}

Übung 4

Lösen Sie den folgenden unbestimmten Grenzwert:

\displaystyle \lim_{x \to +\infty} \cfrac{5x+8}{-5x+2}

In diesem Problem wird die unendliche unbestimmte Form über Unendlich aus dem Quotienten zweier Polynome gleichen Grades erhalten, daher ist das Ergebnis der unbestimmten Grenze die Division ihrer Hauptkoeffizienten:

\displaystyle \lim_{x \to +\infty} \cfrac{5x+8}{-5x+2} = \cfrac{5(+\infty)}{-5(+\infty)} = \cfrac{+\infty}{-\infty}=\cfrac{5}{-5}= \bm{-1}

Übung 5

Berechnen Sie den folgenden Grenzwert mindestens bis ins Unendliche:

\displaystyle \lim_{x \to -\infty} \cfrac{x^2+3x+5}{x^4-x-6}

Der Grad des algebraischen Ausdrucks des Zählers ist kleiner als der Grad des Ausdrucks des Nenners, daher ergibt die Unbestimmtheit +∞/+∞ 0:

\displaystyle \lim_{x \to -\infty} \cfrac{x^2+3x+5}{x^4-x-6} = \cfrac{(-\infty)^2}{(-\infty)^4} = \cfrac{+\infty}{+\infty}= \bm{0}

Übung 6

Lösen Sie den folgenden unbestimmten Grenzwert einer Funktion mit Wurzeln:

\displaystyle\lim_{x\to +\infty}\frac{\sqrt[3]{x^7-4x^3}}{x^2+5x}

Der Ausdruck für den Zähler steht unter einer Wurzel, daher ist sein Grad 7/3. Andererseits ist das Polynom im Nenner quadratisch. Und da 7/3>2, ergibt der Grenzwert plus Unendlich:

\displaystyle \lim_{x \to +\infty}\frac{\sqrt[3]{x^7-4x^3}}{x^2+5x}=\frac{\sqrt[3]{(+\infty)^7}}{(+\infty)^2}=\frac{+\infty}{+\infty}=+\infty

Übung 7

Bestimmen Sie den Grenzwert bis Unendlich der folgenden Funktion mit Brüchen:

\displaystyle\lim_{x \to +\infty} \cfrac{-2x^2}{5-4x}

In dieser Übung erhält man die Unbestimmtheit minus Unendlich dividiert durch minus Unendlich, wobei der Grad des Zählers größer als der Grad des Nenners ist, also:

\displaystyle \lim_{x \to +\infty} \cfrac{-2x^2}{5-4x} = \cfrac{-2(+\infty)^2}{-4(+\infty)} = \cfrac{-2(+\infty)}{-\infty}= \cfrac{-\infty}{-\infty} =\bm{+\infty}

Übung 8

Finden Sie den Grenzwert mindestens ins Unendliche der folgenden Funktion:

\displaystyle \lim_{x \to -\infty} \cfrac{9x}{4-x^2}

Das Nennerpolynom ist quadratisch, während das Zählerpolynom linear ist. Daher ergibt die Unendlichkeit der Unbestimmtheit dividiert durch die Unendlichkeit 0.

\displaystyle \lim_{x \to -\infty} \cfrac{9x}{4-x^2} = \cfrac{9(-\infty)}{-(-\infty)^2} = \cfrac{-\infty}{-(+\infty)}=\cfrac{-\infty}{-\infty}= \bm{0}

Übung 9

Lösen Sie den mindestens unendlichen Grenzwert der folgenden Funktion:

\displaystyle \lim_{x \to -\infty} \cfrac{-2x^3-3x}{-3x^2+4x-1}

Der Zähler hat einen größeren Grad als der Nenner, daher ist das Ergebnis der unbestimmten Form ∞/∞ unendlich. Darüber hinaus ist das Unendlichkeitszeichen negativ, da das Positive geteilt durch das Negative das Negative ergibt:

\displaystyle \lim_{x \to -\infty} \cfrac{-2x^3-3x}{-3x^2+4x-1} = \cfrac{-2(-\infty)^3}{-3(-\infty)^2} =\cfrac{-2(-\infty)}{-3(+\infty)}= \cfrac{+\infty}{-\infty}= \bm{-\infty}

Übung 10

Lösen Sie den folgenden Grenzwert mit unendlicher Unbestimmtheit zwischen Unendlichkeit:

\displaystyle\lim_{x \to +\infty}\cfrac{2^x-4}{-2x^6+x^4}

Die Exponentialfunktion ist von höherer Ordnung als die Polynomfunktion, daher ergibt der Grenzwert Unendlich. Wenn man jedoch das Positive durch das Negative dividiert, erhält man ein negatives Unendlichkeitszeichen:

\displaystyle\lim_{x \to +\infty}\frac{2^x-4}{-2x^6+x^4}=\frac{2^{+\infty}}{-2(+\infty)^6}=\frac{+\infty}{-\infty}=\bm{-\infty}

Übung 11

Berechnen Sie den folgenden Grenzwert:

\displaystyle \lim_{x \to -\infty} \cfrac{x^3-5x}{-x^3-5x^2}

In diesem Problem wird die Unbestimmtheit unendlich auf Unendlich gelöst, indem die dominanten Koeffizienten der beiden Polynome dividiert werden, da sie den gleichen Grad haben:

\displaystyle \lim_{x \to -\infty} \cfrac{x^3-5x}{-x^3-5x^2} = \cfrac{(-\infty)^3}{-(-\infty)^3} = \cfrac{-\infty}{-(-\infty)}= \cfrac{-\infty}{+\infty}=\cfrac{1}{-1}=\bm{-1}

Übung 12

Lösen Sie den Grenzwert der folgenden Funktion, wenn x gegen Unendlich geht:

\displaystyle \lim_{x \to +\infty} \cfrac{(x+3)^2}{x}

Obwohl die Unbekannte im Zähler nicht direkt quadriert wird, können wir bei der Lösung nach der bemerkenswerten Identität deutlich erkennen, dass der Grad des Zählers größer ist als der Grad des Nenners. Noch:

\displaystyle \lim_{x \to +\infty} \cfrac{(x+3)^2}{x}=\lim_{x \to +\infty} \cfrac{x^2+9+6x}{x} = \cfrac{(+\infty)^2}{+\infty} = \cfrac{+\infty}{+\infty} = \bm{+\infty}

Übung 13

Berechnen Sie den Grenzwert der folgenden Funktion mit einer Kubikwurzel ins Unendliche:

\displaystyle \lim_{x \to +\infty} \cfrac{\sqrt[3]{8x^3+1}}{-4x}

Der Zähler besteht aus einer Kubikwurzel, sein Grad ist also 3/3=1. Dann ist der Grad des Zählers gleich dem des Nenners, sodass die unendliche Unbestimmtheit zwischen Unendlichkeit wie folgt aufgelöst wird:

\displaystyle \lim_{x \to +\infty} \cfrac{\sqrt[3]{8x^3+1}}{-4x}= \cfrac{\sqrt[3]{8(+\infty)^3}}{-4(\infty)}= \cfrac{+\infty}{-\infty} = \cfrac{\sqrt[3]{8}}{-4}=\cfrac{2}{-4}=\bm{-}\mathbf{\cfrac{1}{2}}

Übung 14

Lösen Sie den Grenzwert der folgenden Funktion ins Unendliche mit zwei Radikalen:

\displaystyle \lim_{x \to +\infty} \cfrac{\sqrt[3]{6x^7+2x^3}}{\sqrt{x^5-3x^4+2x}}

Der Grad des Zählers ist 7/3 = 2,33 und der Grad des Nenners ist 5/2 = 2,5. Da der Grad des Zählers kleiner ist als der Grad des Nenners, ist die unbestimmte Unendlichkeitsgrenze zwischen Unendlich 0:

\displaystyle \lim_{x \to +\infty} \cfrac{\sqrt[3]{6x^7+2x^3}}{\sqrt{x^5-3x^4+2x}}=\cfrac{\sqrt[3]{6(+\infty)^7}}{\sqrt{(+\infty)^5}}=\cfrac{+\infty}{+\infty}=\bm{0}

Übung 15

Berechnen Sie den folgenden Grenzwert:

\displaystyle \lim_{x \to +\infty} \cfrac{\sqrt[5]{x^7-2x^5-1}}{4^{x-2}+3x}

Unabhängig vom Grad des Zählers ist das Ergebnis der unbestimmten Form Unendlich über Unendlich 0, da wir im Nenner eine Exponentialfunktion haben:

\displaystyle \lim_{x \to +\infty} \cfrac{\sqrt[5]{x^7-2x^5-1}}{4^{x-2}+3x}=\cfrac{\sqrt[5]{(+\infty)^7}}{4^{+\infty-2}}=\cfrac{+\infty}{+\infty}=\bm{0}

Kommentar verfassen

Deine E-Mail-Adresse wird nicht veröffentlicht. Erforderliche Felder sind mit * markiert

Nach oben scrollen