Hier erfahren Sie, was Polynomfunktionen sind und welche Arten von Polynomfunktionen es gibt. Darüber hinaus erklären wir auch die Eigenschaften von Polynomfunktionen.
Was ist eine Polynomfunktion?
Eine Polynomfunktion ist eine Funktion, deren algebraischer Ausdruck ein Polynom ist , d. h. eine Polynomfunktion wird durch die Addition oder Subtraktion einer endlichen Anzahl von Termen unterschiedlichen Grades definiert.
Daher wird eine Polynomfunktion mathematisch durch den folgenden Ausdruck beschrieben:
![]()
Andererseits können Polynomfunktionen auch mit der folgenden Formel definiert werden:
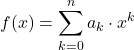
wo die Bedingungen
![]()
Und
![]()
sind jeweils der Koeffizient und die Variable jedes Monoms, das die Polynomfunktion bildet.
Der Begriff
![]()
, Hauptterm genannt, gibt den Grad der Polynomfunktion an, da es sich um das Monom höchsten Grades der Funktion handelt. Mit anderen Worten: Der Exponent mit dem größten Wert ist derjenige, der den Grad der Polynomfunktion angibt.
Obwohl wir weiter unten weitere Merkmale von Polynomfunktionen sehen werden, besteht der Definitionsbereich jeder Polynomfunktion ausschließlich aus reellen Zahlen.
Arten von Polynomfunktionen
Angesichts der Definition der Polynomfunktion werden wir nun sehen, welche Arten von Polynomfunktionen es gibt.
konstante Funktion
Die konstante Funktion ist eine Polynomfunktion vom Grad 0, also ein Funktionstyp, der für jeden Wert der unabhängigen Variablen (x) immer das gleiche Bild annimmt.
Der allgemeine Ausdruck für die konstante Funktion lautet wie folgt:
![]()
Beispielsweise sind die folgenden drei Funktionen Konstanten oder Polynomfunktionen vom Grad Null:
![]()
Die grafische Darstellung einer konstanten Funktion ist eine horizontale Linie (parallel zur x-Achse) mit einem Wert gleich der Konstante.

Weitere Funktionen zu diesem Funktionstyp finden Sie unter folgendem Link:
➤ Siehe: Eigenschaften der konstanten Funktion
Lineare Funktion
Eine lineare Funktion , auch affine Funktion genannt, ist eine Polynomfunktion ersten Grades. Somit kann eine Polynomfunktion dieser Art nur aus einem linearen Term und einem unabhängigen Term bestehen:
![]()
Gold
![]()
ist die Steigung der Geraden und
![]()
ist der y-Achsenabschnitt, also dort, wo die Funktion die Y-Achse schneidet.
Beispiele für lineare Funktionen oder Polynomfunktionen ersten Grades:
![]()
Einige unterscheiden die lineare Funktion von der affinen Funktion, je nachdem, ob die Funktion ihren Term hat
![]()
oder nicht, da es sich um die affine Funktion mit dem Achsenabschnitt und die lineare Funktion ohne handelt.
Bei der grafischen Darstellung linearer Funktionen handelt es sich immer um Linien, deren Neigungsgrad vom Wert der Steigung der Funktion abhängt.
Unten sehen Sie grafisch die Polynomfunktion ersten Grades
![]()

Um jedoch eine lineare Funktion grafisch darzustellen, müssen Sie sich über mehrere Konzepte im Klaren sein. Im folgenden Link finden Sie die Schritt-für-Schritt-Erklärung, wie Sie eine Polynomfunktion dieses Typs grafisch darstellen:
➤ Siehe: Grafische Darstellung einer linearen Funktion
Quadratische Funktion
Eine quadratische Funktion ist eine Polynomfunktion vom Grad 2, also eine Funktion, deren Term höheren Grades zweiten Grades ist.
Daher lautet die Formel für eine quadratische Funktion:
![]()
Gold
![]()
ist der quadratische Term,
![]()
der lineare Term und
![]()
der unabhängige Term der Polynomfunktion.
Beispiele für quadratische Funktionen oder quadratische Polynomfunktionen:
![]()
Der Graph einer quadratischen Funktion ist immer eine Parabel und seine Form hängt vom Vorzeichen des führenden Koeffizienten ab.
![]()
- Wenn der Koeffizient

positiv ist, ist die quadratische Funktion konvex (geformt wie

).
- Stattdessen, wenn der Koeffizient

negativ ist, ist die quadratische Funktion konkav (geformt wie

).


Mit dem Vorzeichen des Hauptkoeffizienten der quadratischen Polynomfunktion können wir also die Form kennen, die ihr Graph annehmen wird, aber um seine genaue grafische Darstellung zu erstellen, muss ein bestimmtes Verfahren befolgt werden. Diese Vorgehensweise können Sie unter folgendem Link einsehen:
➤ Siehe: Grafische Darstellung einer quadratischen Funktion
kubische Funktion
Eine kubische Funktion ist eine Polynomfunktion dritten Grades. Daher wird diese Art von Polynomfunktionen algebraisch wie folgt ausgedrückt:
![]()
Beispiele für kubische Funktionen oder Polynomfunktionen dritten Grades:
![]()
![]()
Grafische Darstellungen kubischer Funktionen entsprechen kubischen Kurven. Um diese Art von Funktionen in einem Diagramm darzustellen, muss jedoch ein kompliziertes Verfahren befolgt werden (es umfasst auch Ableitungen). Wie es geht, können Sie hier sehen:
➤ Siehe: So stellen Sie eine Funktion dar
Wie Sie sehen, gibt es tatsächlich unendlich viele Arten von Polynomfunktionen, da ein Polynom unendlich viele Terme haben kann. So ähnelt beispielsweise eine quartische Funktion einer kubischen Funktion, jedoch mit dem Zusatz eines quadratischen Termes. Wichtig ist, dass Sie verstehen, dass der Typ einer Polynomfunktion durch den Grad der Funktion gekennzeichnet ist.
Eigenschaften von Polynomfunktionen
Polynomfunktionen haben die folgenden Eigenschaften:
- Der Definitionsbereich jeder Polynomfunktion ist die Menge der reellen Zahlen.
![]()
- Alle Polynomfunktionen sind stetig.
- Polynomfunktionen mit einem Grad größer als 1 haben keine Asymptoten.
- Unabhängig von der Art der Polynomfunktion liegt der einzige Schnittpunkt mit der Ordinatenachse (Y-Achse) auf der Höhe ihres unabhängigen Termes, also an folgendem Punkt:
![]()
- Andererseits schneidet eine Polynomfunktion die Abszissenachse (X-Achse) höchstens so oft wie der Grad der Funktion.
- Wenn eine Polynomfunktion nur Terme geraden Grades hat, bedeutet dies, dass sie symmetrisch zur OY-Achse ist. Wenn eine Polynomfunktion hingegen nur Terme ungeraden Grades aufweist, bedeutet dies, dass die Funktion symmetrisch zum Koordinatenursprung ist.
- Die Anzahl der relativen Extrema (Maximum oder Minimum) einer Polynomfunktion beträgt höchstens den Grad des Polynoms der Funktion minus 1.
- Die Anzahl der Wendepunkte einer Polynomfunktion ist höchstens gleich dem Grad des Polynoms der Funktion minus 2.
- Operationen können mit Polynomfunktionen durchgeführt werden:
- Die Summe zweier Polynomfunktionen ergibt eine weitere Polynomfunktion.
- Das Produkt zweier Polynomfunktionen führt zu einer weiteren Polynomfunktion.
- Die Multiplikation einer Polynomfunktion mit einem Skalar (reelle Zahl) führt zu einer ähnlichen Polynomfunktion, deren Graph jedoch reduziert oder erweitert ist.
- Die Zusammensetzung zweier Polynomfunktionen ist gleich einer anderen Polynomfunktion.