In diesem Artikel erklären wir, was symmetrische Funktionen sind (gerade und ungerade Funktionen) und wie man die Symmetrie einer Funktion untersucht. Sie werden auch in der Lage sein, die Eigenschaften dieser Art von Funktionen zu sehen und schließlich können Sie mit Übungen üben, die Schritt für Schritt zu symmetrischen Funktionen gelöst werden.
Was ist eine symmetrische Funktion?
Eine symmetrische Funktion ist eine Funktion, in deren grafischer Darstellung eine Symmetrieachse zu finden ist. Es gibt zwei Arten von symmetrischen Funktionen: gerade Funktionen, symmetrisch zur Y-Achse, und ungerade Funktionen, symmetrisch zum Koordinatenursprung.
Denken Sie daran, dass eine Symmetrieachse eine imaginäre Linie ist, die alles in zwei Teile teilt, sodass ihre gegenüberliegenden Punkte den gleichen Abstand voneinander haben.
sogar Funktionen
Gerade Funktionen sind Funktionen, die symmetrisch zur y-Achse sind, das heißt, die Y-Achse ist eine Symmetrieachse der Funktion.
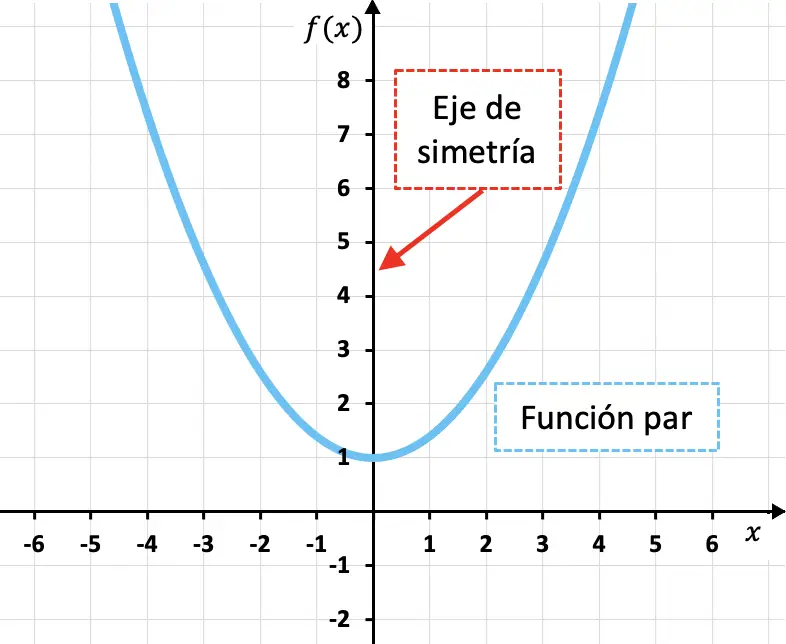
Wie Sie in der oben gezeigten quadratischen Funktion sehen können, ist das Bild einer geraden Funktion für jeden Wert der unabhängigen Variablen (x) äquivalent zum Bild der Funktion für den entgegengesetzten Wert (-x). Mit anderen Worten: Mathematisch gesehen ist eine Funktion gerade, wenn sie die folgende Bedingung erfüllt:
![]()
Gerade Funktionen sind eine Art symmetrischer Funktionen. Sehen wir uns nun an, wie ungerade Funktionen aussehen.
seltsame Funktionen
Ungerade Funktionen sind Funktionen, die bezüglich des Koordinatenursprungs, also bezüglich des Punktes (0,0), symmetrisch sind.
Unten sehen Sie eine seltsame Funktion grafisch dargestellt:
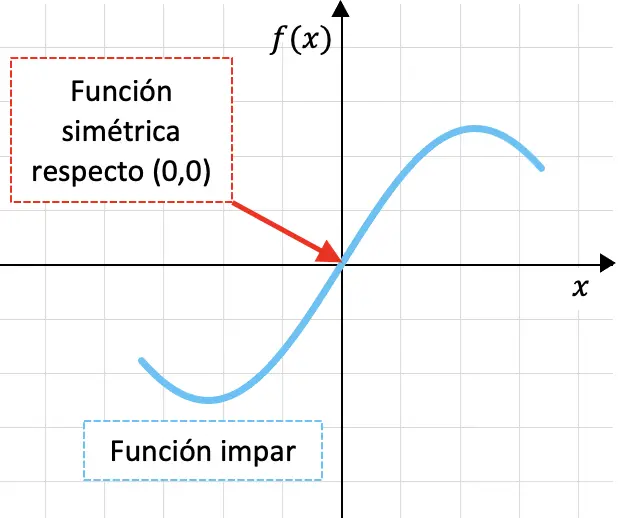
Die Tatsache, dass eine Funktion symmetrisch zum Koordinatenursprung ist, bedeutet, dass sich der Graph der Funktion überlappen würde, wenn wir den Graphen der Funktion zuerst durch die OY-Achse und dann durch die OX-Achse falten würden.
Algebraisch gesehen ist eine Funktion ungerade, wenn die folgende Beziehung zwischen ihren Bildern erfüllt ist:
![]()
Die Kenntnis der Symmetrie einer Funktion ist für deren Darstellung sehr nützlich, denn wenn wir nur eine Hälfte des Graphen kennen, können wir schnell den anderen Teil zeichnen.
So finden Sie die Symmetrie einer Funktion
Um die Symmetrie einer Funktion zu untersuchen, müssen wir das Bild von berechnen
![]()
, das heißt, es ist notwendig zu berechnen
![]()
Abhängig vom Ergebnis des Bildes ist die Symmetrie der Funktion also:
- wenn es gefüllt ist
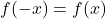
, die Funktion ist gerade und daher symmetrisch bezüglich der Y-Achse.
- wenn es gefüllt ist
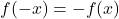
, die Funktion ist ungerade und daher symmetrisch in Bezug auf den Koordinatenursprung.
- Wenn keine der oben genannten Bedingungen erfüllt ist, handelt es sich um eine asymmetrische Funktion (sie hat keine Symmetrieachse).
Lassen Sie uns zum Beispiel die Symmetrie der folgenden kubischen Funktion analysieren:
![]()
Um die Symmetrie der Funktion zu untersuchen, berechnen wir
![]()
![]()
Der resultierende algebraische Ausdruck entspricht dem ursprünglichen Funktionsausdruck, hat jedoch das Vorzeichen geändert, oder mit anderen Worten, die folgende Gleichheit ist erfüllt:
![]()
Die Funktion ist daher ungerade und daher symmetrisch bezüglich des Koordinatenursprungs (0,0).
Eigenschaften symmetrischer Funktionen
Symmetrische Funktionen haben die folgenden Eigenschaften:
- Die Summe zweier gerader/ungerade Funktionen ist gleich einer anderen geraden/ungerade Funktion.
- Das Produkt zweier gerader oder zweier ungerader Funktionen ergibt eine gerade Funktion.
- Die Ableitung einer geraden/ungerade Funktion ist eine gerade/ungerade Funktion.
- Die Zusammensetzung zwischen zwei geraden/ungerade Funktionen entspricht einer geraden/ungerade Funktion.
- Die einzige Funktion, die sowohl gerade als auch ungerade, also symmetrisch zur OY-Achse und zum Ursprung ist, ist die Funktion
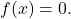
Probleme der Symmetrie einer Funktion gelöst
Übung 1
Finden Sie die Symmetrie der folgenden Funktion:
![]()
Um die Symmetrie der Funktion zu berechnen, müssen wir sie auswerten
![]()
![]()
Jede Potenz einer negativen Zahl, erhöht auf einen Exponenten, ergibt eine positive Zahl, daher gilt in diesem Fall die folgende Gleichung:
![]()
Die Funktion ist daher gerade und daher symmetrisch um die y-Achse (Y-Achse).
Übung 2
Studieren Sie die Symmetrie der folgenden rationalen Funktion:
![]()
Um die Symmetrie der Funktion zu bestimmen, tun wir dies
![]()
![]()
Bei diesem Problem ist keine Symmetriebedingung erfüllt, da das Bild von
![]()
ist ungleich zu
![]()
noch zu
![]()
![]()
Die Funktion hat also keine Symmetrieachse, sondern ist eine asymmetrische Funktion.
Übung 3
Berechnen Sie die Symmetrie der folgenden Funktion:
![]()
Um die Symmetrie der Funktion zu analysieren, müssen wir berechnen
![]()
![Rendered by QuickLaTeX.com \begin{aligned}f(-x)&=2(-x)|(-x)|\\[2ex]&=-2x|-x|\\[2ex]&=-2x|x|\\[2ex]&=-(2x|x|)\\[2ex]&=-f(x)\end{aligned}](https://mathority.org/wp-content/ql-cache/quicklatex.com-d939238f353c0ab70492a66466dd0569_l3.png)
In diesem Fall ist der resultierende Ausdruck wie der ursprüngliche Ausdruck, jedoch mit einem Vorzeichenwechsel, sodass die folgende Gleichung erfüllt ist:
![]()
Die Funktion ist daher ungerade und daher symmetrisch bezüglich des Koordinatenursprungs (0,0).