Begrenzte Funktionen

In diesem Artikel erklären wir, was begrenzte (obere und untere) Funktionen sind. Darüber hinaus zeigen wir Ihnen, was es bedeutet, dass eine Funktion auf einen Punkt beschränkt ist, und schließlich erfahren Sie, welche Eigenschaften diese Art von Funktion hat.

Was ist eine beschränkte Funktion?

Eine begrenzte Funktion ist eine Funktion, deren Graph innerhalb von Grenzen liegt. Das heißt, eine Funktion ist nach oben beschränkt, wenn es eine Zahl K gibt, so dass es keinen Wert der Funktion größer als K (f(x)≤K) gibt, und eine Funktion ist nach unten beschränkt, wenn es eine Zahl K gibt, so dass es keinen Wert der Funktion gibt, der größer als K ist (f(x)≤K). ist kleiner als alle Werte der Funktion (f(x)≥K). Daher ist eine beschränkte Funktion eine Funktion, die nach oben und unten beschränkt ist.

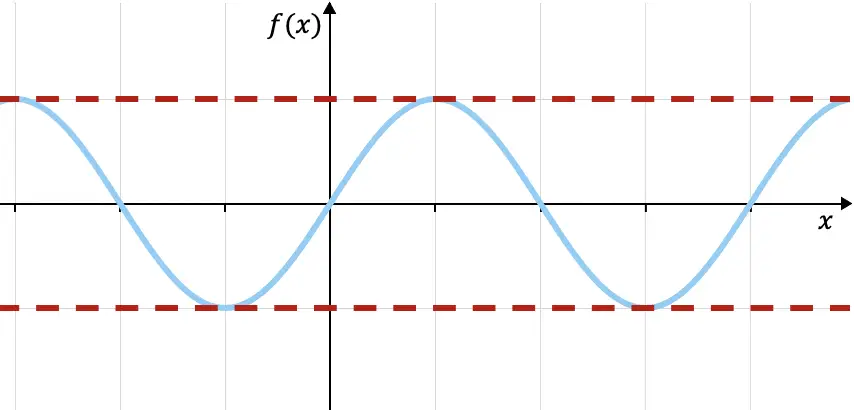
Beispielsweise ist die oben dargestellte trigonometrische Sinusfunktion oben durch f(x)=1 und unten durch f(x)=-1 (rot gepunktete Linien) begrenzt, da alle Werte der Die Funktion liegt innerhalb dieser beiden Grenzen. Weitere Eigenschaften dieser Funktion finden Sie unter folgendem Link:

➤ Siehe: Eigenschaften der Sinusfunktion

Funktion nach oben beschränkt

Allerdings sind nicht alle Funktionen nach oben und unten beschränkt, eine Funktion kann nur nach oben oder unten beschränkt sein.

Bei den oben beschriebenen begrenzten Funktionen handelt es sich um solche, die einen bestimmten Wert nicht überschreiten, d. h. die folgende Bedingung ist erfüllt:

$f(x)\leq K$

wobei der Wert K die Obergrenze der Funktion ist.

Beispielsweise ist die folgende Parabel oben durch K=7 begrenzt, die Funktion ist jedoch unten nicht begrenzt, da ihre Zweige bis ins Unendliche reichen.

Wenn die Funktion durch K=7 begrenzt ist, ist sie logischerweise auch durch K=8 und höhere Werte begrenzt.

Die kleinste Obergrenze wird Obergrenze genannt und durch sup(f) dargestellt. Wenn die Funktion außerdem die Obergrenze in ihrem Bereich erreicht, sagen wir, dass dieser Punkt das absolute Maximum der Funktion ist.

➤ Siehe: Was sind die Maxima und Minima einer Funktion?

In unserem Fall ist die Funktion geometrisch durch K=7 begrenzt, sie ist also das obere Extrem und das absolute Maximum der Funktion.

Funktion unten abgegrenzt

Die unten abgegrenzten Funktionen sind diejenigen, deren Wert nicht kleiner als eine bestimmte Zahl ist, d. h. sie erfüllen den folgenden mathematischen Ausdruck:

$f(x)\geq K$

Wobei der K-Wert die untere Grenze der Funktion ist.

Unten sehen Sie die grafische Darstellung einer Exponentialfunktion, die unten durch K=3 begrenzt ist:

Offensichtlich ist die Funktion auch durch Werte kleiner als K=3 begrenzt.

Wie zuvor wird die größte Untergrenze als Untergrenze bezeichnet und durch inf(f) dargestellt. Wenn die Funktion außerdem das untere Extrem in ihrem Bereich erreicht, sagen wir, dass dieser Punkt das absolute Minimum der Funktion ist.

In diesem Fall ist K=3 nicht das absolute Minimum der Funktion, da die Funktion diesen Wert im Unendlichen erreicht und sich daher außerhalb ihres Definitionsbereichs befindet. Mit anderen Worten, f(x)=3 ist einehorizontale Asymptote der Funktion .

Es gibt einen Satz, mit dem Sie ohne ihre grafische Darstellung feststellen können, ob eine Funktion oben und unten beschränkt ist. Klicken Sie hier, um zu sehen, was der Satz von Weierstrass ist.

➤ Siehe: Satz von Weierstraß

An einem Punkt begrenzte Funktion

Wir haben gerade den Begriff der Beschränkung einer Funktion im Allgemeinen untersucht, aber es ist auch möglich zu analysieren, ob eine Funktion in einer kleineren Umgebung, also in einem Teil der Funktion, beschränkt ist oder nicht.

$a$

ist ein Punkt im Bereich der Funktion und

$r$

Wenn wir einen beliebigen Wert angeben, sagen wir, dass die Funktion an dem Punkt nach oben/unten beschränkt ist

$a$

wenn es eine Umgebung gibt

$V(a,r)$

wobei die Funktion nach oben/unten beschränkt ist.

Daher ist eine Funktion im Punkt beschränkt

$a$

wenn es in einer Nachbarschaft oben und unten abgegrenzt ist

$V(a,r).$

Wenn eine Funktion allgemein beschränkt ist, ist sie natürlich auch an jedem ihrer Punkte beschränkt. Das Gegenteil ist jedoch falsch, das heißt, dass eine Funktion an jedem ihrer Punkte beschränkt sein kann, nicht aber über ihren gesamten Definitionsbereich.

Beispielsweise ist die folgende affine Funktion an jedem ihrer Punkte teilweise beschränkt, es handelt sich jedoch nicht um eine beschränkte Funktion.

Eigenschaften beschränkter Funktionen

Begrenzte Funktionen haben die folgenden Eigenschaften:

Ja
$f(x)$

Und

$g(x)$

sind zwei beschränkte Funktionen, die Addition (oder Subtraktion) der beiden Funktionen

$f(x)\pm g(x)$

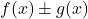
ist ebenfalls eine beschränkte Funktion.
Ja
$f(x)$

Und

$g(x)$

sind zwei beschränkte Funktionen, das Produkt der beiden Funktionen

$f(x)\cdot g(x)$

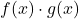
ist zufällig auch eine beschränkte Funktion.
Wenn eine Funktion eine vertikale Asymptote hat, kann sie nicht vollständig beschränkt werden. Andererseits kann die Funktion nach oben oder unten beschränkt sein.
Jede stetige und beschränkte Funktion auf einem Intervall ist integrierbar.