Auf dieser Seite finden Sie alles über den Tangens hyperbolicus: seine Formel, seine grafische Darstellung, alle seine Eigenschaften, …
Hyperbolische Tangensformel
Die hyperbolische Tangensfunktion ist eine der wichtigsten hyperbolischen Funktionen und wird durch das Symbol tanh(x) dargestellt. Mathematisch gesehen ist der hyperbolische Tangens gleich dem hyperbolischen Sinus dividiert durch den hyperbolischen Kosinus.
![]()
Aus der hyperbolischen Sinusformel und der hyperbolischen Kosinusformel können wir zu folgendem Ausdruck gelangen:
![]()
Daher hängt die hyperbolische Tangensfunktion mit der Exponentialfunktion zusammen. Unter dem folgenden Link können Sie alle Merkmale dieser Funktionstypen sehen:
➤ Siehe: Eigenschaften von Exponentialfunktionen
Grafische Darstellung des hyperbolischen Tangens
Aus seiner Formel können wir die hyperbolische Tangensfunktion grafisch darstellen:
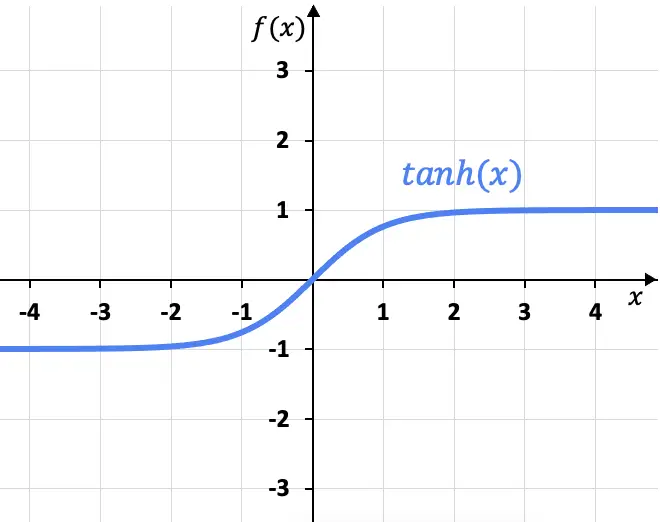
Wie Sie aus der Grafik ersehen können, hat die hyperbolische Tangensfunktion zwei horizontale Asymptoten bei x=+1 und x=-1, da der Grenzwert der Funktion bei Annäherung von x an Plus-Unendlich x=+1 ergibt und der Grenzwert bei Minus-Unendlich liegt ergibt x=-1.
Andererseits hat der Graph des Tangens hyperbolicus nichts mit dem Graphen des Tangens (trigonometrische Funktion) zu tun, der eine periodische Funktion ist. Die grafische Darstellung des Tangens und wie er sich vom hyperbolischen Tangens unterscheidet, können Sie im folgenden Link sehen:
➤ Siehe: Grafische Darstellung der Tangensfunktion
Eigenschaften des hyperbolischen Tangens
Die hyperbolische Tangensfunktion hat die folgenden Eigenschaften:
- Der Definitionsbereich der hyperbolischen Tangensfunktion sind alle reellen Zahlen.
![]()
- Im Gegensatz dazu ist der Pfad bzw. Bereich der hyperbolischen Tangensfunktion auf Werte zwischen -1 und +1 (nicht inklusive) beschränkt.
![]()
- Der hyperbolische Tangens ist eine stetige, bijektive und ungerade Funktion (symmetrisch zum Koordinatenursprung).
![]()
- Die Funktion schneidet die X-Achse und die Y-Achse im Koordinatenursprung.
![]()
- Die Grenzen der hyperbolischen Tangensfunktion auf plus/minus unendlich ergeben +1/-1. Daher hat die Funktion eine horizontale Asymptote bei x=+1 und eine weitere horizontale Asymptote bei x=-1.
![]()
![]()
- Der Tangens hyperbolicus ist über seinen gesamten Bereich streng steigend, hat also keine relativen Extrema (weder Maximum noch Minimum).
- Allerdings ändert sich die Funktion am Punkt x = 0 von konvex zu konkav, sodass x = 0 ein Wendepunkt der Funktion ist.
- Die Umkehrung der hyperbolischen Tangensfunktion wird als Argument des hyperbolischen Tangens (oder hyperbolischen Arkustangens) bezeichnet und ihre Formel lautet wie folgt:
![]()
- Die Ableitung der hyperbolischen Tangensfunktion ist 1 dividiert durch das Quadrat des hyperbolischen Kosinus:
![]()
- Das Integral der hyperbolischen Tangensfunktion ist der natürliche Logarithmus des hyperbolischen Kosinus:
![]()
- Der hyperbolische Tangens der Summe zweier verschiedener Zahlen kann durch Anwendung der folgenden Gleichung berechnet werden:
![]()
- Das Taylor-Polynom oder die hyperbolische Tangensreihe hat den Konvergenzradius
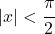
und entspricht dem folgenden Ausdruck:
![]()
Gold
![]()
ist die Bernoulli-Zahl .