Hyperbolische Kosinusfunktion

Hier erfahren Sie alles über die hyperbolische Kosinusfunktion: Wie lautet ihre Formel, ihre grafische Darstellung, ihre Eigenschaften, die mathematischen Beziehungen zu anderen Funktionen usw.

Hyperbolische Kosinusformel

Die hyperbolische Kosinusfunktion ist eine der wichtigsten hyperbolischen Funktionen und wird durch das Symbol cosh(x) dargestellt. Der hyperbolische Kosinus ist gleich der Summe von e ^x plus e ^-x dividiert durch 2.

Daher lautet die Formel für den hyperbolischen Kosinus:

$\displaystyle\text{cosh}(x)=\cfrac{e^{x}+e^{-x}}{2}$

Somit hängt der hyperbolische Kosinus mathematisch mit der Exponentialfunktion zusammen. Im folgenden Link können Sie die Eigenschaften dieses Funktionstyps sehen:

➤ Siehe: Eigenschaften der Exponentialfunktion

Grafische Darstellung des hyperbolischen Kosinus

Die grafische Darstellung der hyperbolischen Kosinusfunktion erfolgt in Form einer quadratischen Funktion (oder Parabel):

➤ Siehe: Grafische Darstellung einer quadratischen Funktion .

In diesem Diagramm können wir deutlich erkennen, dass der hyperbolische Kosinus eine gerade Funktion ist, da er symmetrisch zur y-Achse ist.

Andererseits unterscheidet sich der Graph des hyperbolischen Kosinus stark von dem des Kosinus (trigonometrische Funktion), der eine periodische Funktion ist. Die grafische Darstellung des Kosinus und alle Unterschiede zum hyperbolischen Kosinus können Sie im folgenden Link sehen:

➤ Siehe: Grafische Darstellung der Kosinusfunktion

Eigenschaften des hyperbolischen Kosinus

Der hyperbolische Kosinus berücksichtigt die folgenden Eigenschaften:

Der Definitionsbereich der hyperbolischen Kosinusfunktion sind alle reellen Zahlen:

$\text{Dom } f = \mathbb{R}$

Stattdessen ist der Bereich (oder Bereich) der hyperbolischen Kosinusfunktion 1 und alle Zahlen größer als 1:

$\text{Im } f= [1,+\infty)$

Der hyperbolische Kosinus ist eine stetige und gerade Funktion.

$\displaystyle \text{cosh}(-x)=\text{cosh}(x)$

Die Funktion schneidet die Y-Achse im Punkt x=0.

$(0,1)$

Andererseits hat die Funktion keinen Schnittpunkt mit der X-Achse.

Die beiden Grenzwerte bis Unendlich (positiv und negativ) der hyperbolischen Kosinusfunktion ergeben plus Unendlich.

$\displaystyle\lim_{x\to+\infty}\text{cosh}(x)=+\infty$

$\displaystyle\lim_{x\to-\infty}\text{cosh}(x)=+\infty$

Der hyperbolische Kosinus nimmt bis x = 0 ab und nimmt von diesem Punkt an auf unbestimmte Zeit zu, sodass die Funktion bei x = 0 ein Minimum hat.

$(0,1)$

Die Funktion ist in ihrem gesamten Definitionsbereich konvex, hat also keinen Wendepunkt.

Die Ableitung der hyperbolischen Kosinusfunktion ist der hyperbolische Sinus:

$f(x)=\text{cosh}(x) \ \longrightarrow \ f'(x)=\text{senh}(x)$

Das Integral der hyperbolischen Kosinusfunktion ist der hyperbolische Sinus:

$\displaystyle \int \text{cosh}(x) \ dx= \text{senh}(x) + C$

Das Taylor-Polynom (oder die Maclaurin-Reihe) der hyperbolischen Kosinusfunktion lautet wie folgt:

$\displaystyle\text{cosh}(x)=1+\cfrac{x^2}{2!}+\cfrac{x^4}{4!}+\cfrac{x^6}{6!}+\dots=\sum_{n=0}^\infty\cfrac{x^{2n}}{(2n)!}$

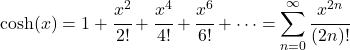
Die Laplace-Transformation der hyperbolischen Kosinusfunktion lautet wie folgt:

$\mathcal{L}\bigl[\text{cosh}(at)\bigr]=\cfrac{s}{s^2-a^2}$

Mathematische Beziehungen des hyperbolischen Kosinus

Als nächstes werden wir sehen, wie der hyperbolische Kosinus aus anderen hyperbolischen Funktionen berechnet werden kann, da sie alle mathematisch verwandt sind.

Die Grundgleichung setzt den hyperbolischen Kosinus mit dem hyperbolischen Sinus in Beziehung:

$\text{cosh}^2(x)-\text{senh}^2(x)=1$

➤ Siehe: Sinus hyperbolicus

Die drei wichtigsten hyperbolischen Funktionen (hyperbolischer Sinus, Cosinus und Tangens) können durch die folgende Gleichung in Beziehung gesetzt werden:

$\text{tanh}(x)=\cfrac{\text{senh}(x)}{\text{cosh}(x)}$

Andererseits kann der hyperbolische Kosinus der Addition (oder Subtraktion) zweier verschiedener Zahlen durch die folgenden Formeln bestimmt werden:

$\text{cosh}(x+y)=\text{cosh}(x)\text{cosh}(y)+\text{senh}(y)\text{senh}(x)$

$\text{cosh}(x-y)=\text{cosh}(x)\text{cosh}(y)-\text{senh}(y)\text{senh}(x)$

Der hyperbolische Kosinus des Doppelten einer Zahl ist gleich der Summe der Quadrate des hyperbolischen Kosinus und des hyperbolischen Sinus dieser Zahl:

$\text{cosh}(2x)=\text{cosh}^2(x)+\text{senh}^2(x)$

Die Addition oder Subtraktion zweier hyperbolischer Kosinuswerte kann mithilfe der folgenden Formeln berechnet werden:

$\displaystyle\text{cosh}(x)+\text{cosh}(y)=2\text{cosh}\left(\frac{x+y}{2}\right)\text{cosh}\left(\frac{x-y}{2}\right)$

$\displaystyle\text{cosh}(x)-\text{cosh}(y)=2\text{senh}\left(\frac{x+y}{2}\right)\text{senh}\left(\frac{x-y}{2}\right)$

Schließlich kann das Quadrat des hyperbolischen Kosinus mit der folgenden Formel berechnet werden:

$\text{cosh}^2(x)=\cfrac{1}{2}\Bigl(\text{cosh}(2x)+1\Bigr)$

Hyperbolische kosinusfunktion

Hyperbolische Kosinusformel

Grafische Darstellung des hyperbolischen Kosinus

Eigenschaften des hyperbolischen Kosinus

Mathematische Beziehungen des hyperbolischen Kosinus

Kommentar verfassen Kommentieren abbrechen