Hyperbolische Sinusfunktion

In diesem Artikel erfahren Sie alles über den Sinus hyperbolicus: Wie lautet seine Formel, seine grafische Darstellung, alle seine Eigenschaften, die Beziehungen zu anderen Funktionen, …

Hyperbolische Sinusformel

Die hyperbolische Sinusfunktion ist eine der wichtigsten hyperbolischen Funktionen und wird durch das Symbol sinh(x) oder sinh(x) dargestellt. Der hyperbolische Sinus ist gleich e ^x minus e ^-x geteilt durch 2.

Die Formel für den Sinus hyperbolicus lautet daher wie folgt:

$\displaystyle\text{senh}(x)=\cfrac{e^{x}-e^{-x}}{2}$

Somit hängt der hyperbolische Sinus mit der Exponentialfunktion zusammen.

➤ Siehe: Eigenschaften der Exponentialfunktion

Grafische Darstellung des hyperbolischen Sinus

Mit der Formel, die wir im vorherigen Abschnitt gesehen haben, können wir eine Tabelle der hyperbolischen Sinuswerte erstellen und die Funktion grafisch darstellen:

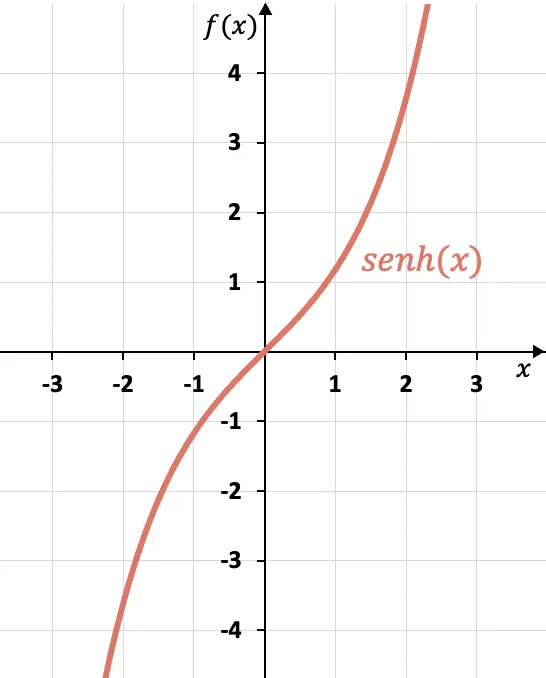
In diesem Diagramm können wir sehen, dass der hyperbolische Sinus eine ungerade Funktion ist, da die gegenüberliegenden x entgegengesetzte Bilder haben, oder mit anderen Worten, der hyperbolische Sinusgraph ist symmetrisch zum Koordinatenursprung (0, 0).

Wie Sie sehen können, unterscheidet sich der hyperbolische Sinusgraph stark von dem des Sinus, der eine periodische Funktion ist. Die grafische Darstellung des Sinus und alle Unterschiede zum hyperbolischen Sinus können Sie im folgenden Link sehen:

➤ Siehe: Grafische Darstellung der Sinusfunktion

Eigenschaften des hyperbolischen Sinus

Der Sinus hyperbolicus hat folgende Eigenschaften:

Der Definitionsbereich der hyperbolischen Sinusfunktion sind alle reellen Zahlen:

$\text{Dom } f = \mathbb{R}$

Auch der Bereich bzw. Bereich der hyperbolischen Sinusfunktion sind allesamt reelle Zahlen.

$\text{Im } f= \mathbb{R}$

Der Sinus hyperbolicus ist eine stetige und ungerade Funktion.

$\displaystyle \text{senh}(-x) =- \text{senh}(x)$

Schnittpunkt der X-Achse und der Y-Achse am selben Schnittpunkt, dem Koordinatenursprung:

$(0,0)$

Der Grenzwert der hyperbolischen Sinusfunktion, wenn x gegen plus/minus unendlich tendiert, ist gleich plus/minus unendlich:

$\displaystyle\lim_{x\to+\infty}\text{senh}(x)=+\infty$

$\displaystyle\lim_{x\to-\infty}\text{senh}(x)=-\infty$

Der Sinus hyperbolicus nimmt im gesamten Bereich streng zu, hat also weder Maxima noch Minima.

Allerdings ändert sie im Punkt x = 0 ihre Krümmung, ist also ein Wendepunkt der Funktion. Für Werte kleiner als x=0 handelt es sich um eine konkave Funktion, für Werte größer als x=0 hingegen um eine konvexe Funktion.

Die Ableitung der hyperbolischen Sinusfunktion ist der hyperbolische Kosinus:

$f(x)=\text{senh}(x) \ \longrightarrow \ f'(x)=\text{cosh}(x)$

Ebenso ist das Integral der hyperbolischen Sinusfunktion der hyperbolische Kosinus:

$\displaystyle \int \text{senh}(x) \ dx= \text{cosh}(x) + C$

Die Taylor-Reihe der hyperbolischen Sinusfunktion entspricht dem folgenden Ausdruck:

$\displaystyle\text{senh}(x)=x+\cfrac{x^3}{3!}+\cfrac{x^5}{5!}+\cfrac{x^7}{7!}+\dots=\sum_{n=0}^\infty\cfrac{x^{2n+1}}{(2n+1)!}$

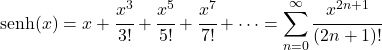
Die Laplace-Transformation der hyperbolischen Sinusfunktion lautet wie folgt:

$\mathcal{L}\bigl[\text{senh}(at)\bigr]=\cfrac{a}{s^2-a^2}$

Mathematische Beziehungen des hyperbolischen Sinus

Der hyperbolische Sinus ist durch die folgenden Gleichungen mit den anderen hyperbolischen Funktionen verknüpft:

Die Grundgleichung setzt den hyperbolischen Sinus mit dem hyperbolischen Kosinus in Beziehung:

$\text{cosh}^2(x)-\text{senh}^2(x)=1$

Daher sind die hyperbolischen Sinus- und Cosinusfunktionen durch die Hyperbelgleichung verknüpft, die x ² -y ² =1 ist. Im Gegensatz zu den trigonometrischen Sinus- und Cosinusfunktionen, die durch die Kreisgleichung (x ² +y ² =1) verknüpft sind.

Die hyperbolischen Funktionen von Sinus, Cosinus und Tangens können durch die folgende Gleichung in Beziehung gesetzt werden:

$\text{tanh}(x)=\cfrac{\text{senh}(x)}{\text{cosh}(x)}$

Andererseits kann der hyperbolische Sinus der Addition oder Subtraktion zweier verschiedener Zahlen mit den folgenden Formeln berechnet werden:

$\text{senh}(x+y)=\text{senh}(x)\text{cosh}(y)+\text{senh}(y)\text{cosh}(x)$

$\text{senh}(x-y)=\text{senh}(x)\text{cosh}(y)-\text{senh}(y)\text{cosh}(x)$

Der hyperbolische Sinus des Doppelten einer Zahl kann durch Anwendung der folgenden mathematischen Beziehung bestimmt werden:

$\text{senh}(2x)=2\text{senh}(x)\text{cosh}(x)$

Die Summe oder Subtraktion zweier hyperbolischer Sinus kann mit den folgenden Formeln ermittelt werden:

$\displaystyle\text{senh}(x)+\text{senh}(y)=2\text{senh}\left(\frac{x+y}{2}\right)\text{cosh}\left(\frac{x-y}{2}\right)$

$\displaystyle\text{senh}(x)-\text{senh}(y)=2\text{senh}\left(\frac{x-y}{2}\right)\text{cosh}\left(\frac{x+y}{2}\right)$

Schließlich kann das Quadrat des hyperbolischen Sinus mit der folgenden Formel berechnet werden:

$\text{senh}^2(x)=\cfrac{1}{2}\Bigl(\text{cosh}(2x)-1\Bigr)$

Hyperbolische sinusfunktion

Hyperbolische Sinusformel

Grafische Darstellung des hyperbolischen Sinus

Eigenschaften des hyperbolischen Sinus

Mathematische Beziehungen des hyperbolischen Sinus

Kommentar verfassen Kommentieren abbrechen