Symmetrische Matrix

Auf dieser Seite finden Sie die Erklärung, was symmetrische Matrizen sind. Außerdem zeigen wir Ihnen, wie Sie schnell erkennen können, ob eine Matrix symmetrisch ist, und geben Ihnen mehrere Beispiele, damit Sie keine Zweifel haben. Außerdem finden Sie hier alle Eigenschaften symmetrischer Matrizen. Und schließlich erklären wir eine besondere Eigenschaft jeder quadratischen Matrix: Sie kann in die Summe einer symmetrischen Matrix und einer antisymmetrischen Matrix zerlegt werden.

Was ist eine symmetrische Matrix?

Die Definition einer symmetrischen Matrix lautet wie folgt:

Eine symmetrische Matrix ist eine quadratische Matrix, deren Transponierte gleich der Matrix selbst ist.

$A^t = A$

Gold

$A^t$

stellt die transponierte Matrix von dar

$A$

Sobald wir das Konzept einer symmetrischen Matrix kennen, werden wir sehen, wie jede symmetrische Matrix leicht identifiziert werden kann:

Wann ist eine Matrix symmetrisch?

Das Erkennen der Struktur einer symmetrischen Matrix ist sehr einfach: Das Element von Zeile i und Spalte j muss mit dem Element von Zeile j und Spalte i identisch sein. Und die Werte der Hauptdiagonale der Matrix können beliebig sein.

Beispiele für symmetrische Matrizen

Hier sind einige Beispiele für symmetrische Matrizen, um Ihnen das Verständnis zu erleichtern:

Beispiel einer symmetrischen Matrix der Ordnung 2 × 2

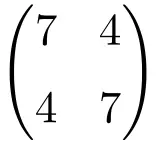
Beispiel einer symmetrischen Matrix der Dimension 2x2

Beispiel einer symmetrischen Matrix der Dimension 3×3

Beispiel einer symmetrischen Matrix der Dimension 3x3

Beispiel einer symmetrischen Matrix der Größe 4×4

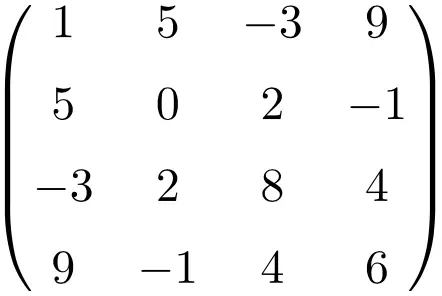
Beispiel einer symmetrischen Matrix der Dimension 4x4

Durch Transponieren dieser drei Matrizen stellen wir sicher, dass sie symmetrisch sind, da die transponierten Matrizen ihren jeweiligen Originalmatrizen äquivalent sind.

Warum wird es eine symmetrische Matrix genannt?

Wenn Sie sich die vorherigen Beispiele genau ansehen, ist die Hauptdiagonale einer symmetrischen Matrix eine Symmetrieachse, oder mit anderen Worten, sie fungiert als Spiegel zwischen den Zahlen über der Diagonale und denen darunter. Aus diesem Grund werden diese Matrizentypen als symmetrisch bezeichnet.

Eigenschaften symmetrischer Matrizen

Die Eigenschaften symmetrischer Matrizen sind wie folgt:

Das Addieren (oder Subtrahieren) zweier symmetrischer Matrizen ergibt eine weitere symmetrische Matrix. Da das Transponieren zweier addierter (oder subtrahierter) Matrizen dem Transponieren jeder Matrix einzeln entspricht:

$\displaystyle \left(A+B\right)^t = A^t+B^t = A+B$

Jede symmetrische Matrix, multipliziert mit einem Skalar, führt auch zu einer anderen symmetrischen Matrix.

Ebenso ist das Matrixprodukt zwischen zwei symmetrischen Matrizen nicht immer gleich einer anderen symmetrischen Matrix, sondern nur dann, wenn die beiden Matrizen vertauscht werden können. Diese Bedingung kann mit der transponierten Matrixmultiplikationseigenschaft bewiesen werden:

$\displaystyle \left(A\cdot B\right)^t = B^t\cdot A^t = BA=AB$

Die Potenz einer symmetrischen Matrix führt zu einer anderen symmetrischen Matrix, solange der Exponent eine ganze Zahl ist.

Offensichtlich sind die Einheitsmatrix und die Nullmatrix Beispiele für symmetrische Matrizen.

Eine zu einer symmetrischen Matrix kongruente Matrix muss auch symmetrisch sein.

Wenn eine symmetrische Matrix regelmäßig oder invertierbar ist, dann ist auch ihre inverse Matrix symmetrisch.

Das Gleiche gilt für die Adjungierte einer symmetrischen Matrix: Die adjungierte Matrix einer symmetrischen Matrix ergibt eine andere symmetrische Matrix als Lösung.

Eine echte symmetrische Matrix ist auch eine Normalmatrix.

Da symmetrische Matrizen ein Sonderfall der hermiteschen Matrizen sind, sind alle Eigenwerte (oder Eigenwerte) einer symmetrischen Matrix reelle Zahlen.

Der Spektralsatz sagt uns, dass alle Matrizen, deren Elemente reell sind, diagonalisierbare Matrizen sind und außerdem die Diagonalisierung mittels einer orthogonalen Matrix erfolgt. Daher sind alle reellen symmetrischen Matrizen orthogonal diagonalisiert.

Andererseits können symmetrische Matrizen mit komplexen Zahlen durch eine einheitliche Matrix diagonalisiert werden.

Die Hesse-Matrix ist immer symmetrisch.

Zerlegung einer quadratischen Matrix in eine symmetrische Matrix und eine antisymmetrische Matrix

Eine Besonderheit quadratischer Matrizen besteht darin, dass sie in die Summe einer symmetrischen Matrix plus einer antisymmetrischen Matrix zerlegt werden können.

Die Formel, die uns dies ermöglicht, lautet wie folgt:

$\displaystyle \begin{array}{c} C = S + A \\[2ex] S = \cfrac{1}{2}\cdot (C+C^t) \qquad A = \cfrac{1}{2} \cdot (C-C^t)\end{array}$

Wobei C die quadratische Matrix ist, die wir zerlegen möchten, C ^t ihre Transponierte und schließlich S und A die symmetrischen bzw. antisymmetrischen Matrizen sind, in die die Matrix C zerlegt wird.

Unten finden Sie eine gelöste Übung, um zu sehen, wie das geht. Zerlegen wir die folgende Matrix:

$\displaystyle C=\begin{pmatrix} 2& -1 \\[1.1ex] 3 &0\end{pmatrix}$

Wir berechnen die symmetrische und antisymmetrische Matrix mit den Formeln:

$\displaystyle S=\cfrac{1}{2}\cdot (C+C^t)= \begin{pmatrix} 2& 1 \\[1.1ex] 1 &0\end{pmatrix}$

$\displaystyle A=\cfrac{1}{2}\cdot (C-C^t)= \begin{pmatrix} 0& -2 \\[1.1ex] 2 &0\end{pmatrix}$

Und wir können überprüfen, ob die Gleichung erfüllt ist, indem wir die beiden Matrizen addieren:

$\displaystyle C=S+A \quad ?$

$\displaystyle\begin{pmatrix} 2& 1 \\[1.1ex] 1 &0\end{pmatrix}+\begin{pmatrix} 0& -2 \\[1.1ex] 2 &0\end{pmatrix}=\begin{pmatrix} 2& -1 \\[1.1ex] 3 &0\end{pmatrix}$

$\displaystyle C=S+A$

✅