▷ Ableitung des Arkustangens (Formel und Beispiele)

In diesem Artikel erfahren Sie, wie Sie den Arkustangens einer Funktion ableiten. Darüber hinaus können Sie Beispiele für diese Art der Ableitung sehen und sogar mit gelösten Übungen zur Ableitung des Arkustangens üben. Abschließend zeigen wir Ihnen noch den Beweis der Formel für die Ableitung des Arkustangens.

Was ist die Ableitung des Arkustangens?

Die Ableitung des Arkustangens von x ist eins über eins plus x zum Quadrat.

$f(x)=\text{arctan}(x) \quad\color{orange}\bm{\longrightarrow}\quad\color{black} f'(x)=\cfrac{1}{1+x^2}$

Daher ist die Ableitung des Arkustangens einer Funktion gleich dem Quotienten aus der Ableitung dieser Funktion geteilt durch eins plus dem Quadrat der Funktion.

$f(x)=\text{arctan}(u) \quad\color{orange}\bm{\longrightarrow}\quad\color{black} f'(x)=\cfrac{u'}{1+u^2}$

In diesem Fall wurde die Funktion durch au dargestellt, also wäre dies die Formel für die Ableitung des Arkustangens der Funktion u.

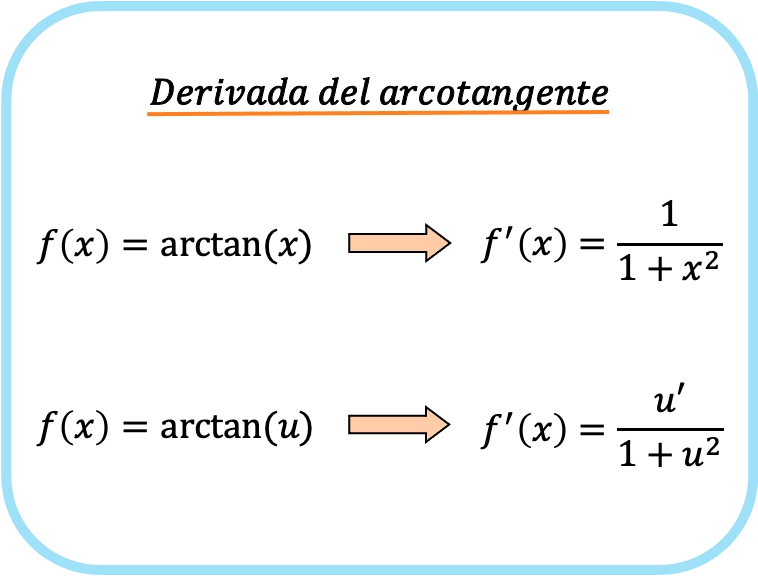
Wie Sie sehen können, ist die Formel für die Ableitung des Umkehrtangens den Formeln für die Ableitungen von Arkussinus und Arkuskosinus sehr ähnlich.

Beispiele für die Ableitung des Arkustangens

Sobald wir die Formel für die Ableitung des Arkustangens kennen, erklären wir die Ableitung mehrerer Beispiele dieser Art trigonometrischer Ableitungen. Auf diese Weise können Sie leichter verstehen, wie der Arkustangens einer Funktion abgeleitet wird.

Beispiel 1: Ableitung des Arkustangens von 2x

$f(x)=\text{arctan}(2x)$

Wir wenden die Formel an, um die Ableitung zu lösen:

$f(x)=\text{arctan}(u) \quad\color{orange}\bm{\longrightarrow}\quad\color{black} f'(x)=\cfrac{u'}{1+u^2}$

Die Ableitung von 2x ist 2, also ist die Arkustangens-Ableitung von 2x 2 über eins plus 2x im Quadrat:

$f(x)=\text{arctan}(2x) \quad\color{orange}\bm{\longrightarrow}\quad\color{black} f'(x)=\cfrac{2}{1+(2x)^2}}=\cfrac{2}{1+ 4x^2}$

Beispiel 2: Ableitung des Arkustangens von x im Quadrat

$f(x)=\text{arctan}(x^2)$

Um das Ergebnis der Ableitung dieses Beispiels zu finden, müssen wir die Formel für die Ableitung des Arkustangens verwenden, die lautet:

$f(x)=\text{arctan}(u) \quad\color{orange}\bm{\longrightarrow}\quad\color{black} f'(x)=\cfrac{u'}{1+u^2}$

Somit ist die Ableitung der Funktion x ² 2x, also ist die Ableitung des Arkustangens von x hoch 2:

$f(x)=\text{arctan}(x^2) \quad\color{orange}\bm{\longrightarrow}\quad\color{black} f'(x)=\cfrac{2x}{1+\left(x^2\right)^2}=\cfrac{2x}{1+x^4}$

Beispiel 3: Ableitung des Arkustangens des Sinus von x

$f(x)=\text{arctan}\bigl(\text{sen}(x)\bigr)$

Um die Ableitung zu berechnen, müssen Sie logischerweise die entsprechende Formel anwenden:

$f(x)=\text{arctan}(u) \quad\color{orange}\bm{\longrightarrow}\quad\color{black} f'(x)=\cfrac{u'}{1+u^2}$

In diesem Fall haben wir eine zusammengesetzte Funktion, also müssen wir die Kettenregel anwenden, um die Ableitung des Arkustangens zu berechnen:

$f(x)=\text{arctan}\bigl(\text{sen}(x)\bigr) \quad\color{orange}\bm{\longrightarrow}\quad\color{black} f'(x)=\cfrac{\text{cos}(x)}{1+\text{sen}^2(x)}$

Gelöste Übungen zur Ableitung des Arkustangens

Leiten Sie die folgenden Arkustangensfunktionen her:

$\text{A) } f(x)=\text{arctan}(x^3)$

$\text{B) } f(x)=\cfrac{\text{arctan}(3x^4)}{2}$

$\text{C) } f(x)=\text{arctan}(x^5-3x^3+10)$

$\text{D) }f(x)=\text{arctan}^3(4x^2)$

$\text{E) }f(x)=\text{arctan}\bigl(\ln(x)\bigr)$

$\text{F) } f(x)=\text{arctan}\left(\sqrt{x^2+2x}\right)$

Sehen Sie sich die Lösung an

$\text{A) } f'(x)=\cfrac{3x^2}{1+\left(x^3\right)^2}=\cfrac{3x^2}{1+x^6}$

$\text{B) } f'(x)=\cfrac{12x^3}{2\left(1+\left(3x^4\right)^2\right)}=\cfrac{6x^3}{1+9x^8}$

$\text{C) } f'(x)=\cfrac{5x^4-9x^2}{1+\left(x^5-3x^3+10\right)^2}$

$\text{D) } f'(x)=3\text{arctan}^2(4x^2)\cdot \cfrac{8x}{1+\left(4x^2\right)^2}=\cfrac{24x\cdot\text{arctan}^2(4x^2)}{1+16x^2}$

$\text{E) } f'(x)=\cfrac{\cfrac{1}{x}}{1+\bigl(\ln(x)\bigr)^2}=\cfrac{1}{x\left(1+\ln^2(x)\right)}$

$\text{F) } f'(x)=\cfrac{1}{1+\left(\sqrt{x^2+2x}\right)^2}\cdot \cfrac{2x+2}{2\sqrt{x^2+2x}}=\cfrac{x+1}{\left(1+x^2+2x\right)\sqrt{x^2+2x}}$

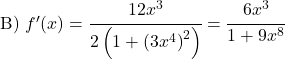
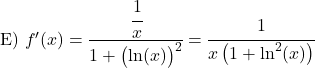
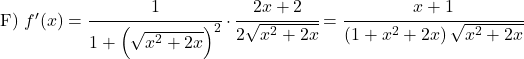
Demonstration der Formel für die Ableitung des Arkustangens

Als nächstes beweisen wir die Formel für die Ableitung des Arkustangens.

$y=\text{arctan}(x)$

Wir wandeln zunächst den Arkustangens in einen Tangens um und machen uns dabei die Tatsache zunutze, dass der Arkustangens die Umkehrfunktion des Tangens ist:

$x=\text{tan}(y)$

Wir unterscheiden die beiden Seiten der Gleichung:

$1=\cfrac{1}{\text{cos}^2(y)}\cdot y'$

Wir löschen und‘:

$y'=\text{cos}^2(y)$

Andererseits wissen wir dank der grundlegenden trigonometrischen Identität, dass die Summe der Quadrate von Sinus und Cosinus gleich 1 ist. Wir können daher den vorherigen Ausdruck in einen Bruch umwandeln:

$\text{sen}^2(y)+\text{cos}^2(y)=1$

$y'=\cfrac{\text{cos}^2(y)}{1}=\cfrac{\text{cos}^2(y)}{\text{sen}^2(y)+\text{cos}^2(y)}$

Wir dividieren alle Terme durch das Quadrat des Kosinus:

$y'=\cfrac{\cfrac{\text{cos}^2(y)}{\text{cos}^2(y)}}{\cfrac{\text{sen}^2(y)}{\text{cos}^2(y)}+\cfrac{\text{cos}^2(y)}{\text{cos}^2(y)}}$

$y'=\cfrac{1}{\cfrac{\text{sen}^2(y)}{\text{cos}^2(y)}+1}$

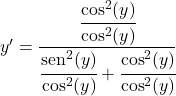
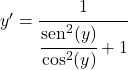
Der Sinus dividiert durch den Cosinus ist gleich dem Tangens, also:

$\text{tan}(x)=\cfrac{\text{sen}(x)}{\text{cos}(x)}$

$y'=\cfrac{1}{\text{tan}^2(y)+1}$

Wie wir oben gesehen haben, ist der Tangens äquivalent zur Variablen x, daher können wir den Ausdruck ersetzen, um die Formel für die Ableitung des Arkustangens zu erhalten:

$y'=\cfrac{1}{x^2+1}$

Ableitung des arkustangens

Was ist die Ableitung des Arkustangens?

Beispiele für die Ableitung des Arkustangens

Beispiel 1: Ableitung des Arkustangens von 2x

Beispiel 2: Ableitung des Arkustangens von x im Quadrat

Beispiel 3: Ableitung des Arkustangens des Sinus von x

Gelöste Übungen zur Ableitung des Arkustangens

Demonstration der Formel für die Ableitung des Arkustangens

Kommentar verfassen Kommentieren abbrechen