Singuläre oder entartete Matrix

Auf dieser Seite erfahren Sie, was es bedeutet, dass eine Matrix singulär oder entartet ist. Darüber hinaus zeigen wir Ihnen einige Beispiele, damit Sie keine Zweifel haben, und erklären abschließend alle Eigenschaften dieser Art von Matrix.

Was ist eine singuläre oder entartete Matrix?

Die Definition einer singulären Matrix, auch entartete Matrix genannt, lautet wie folgt:

Eine singuläre oder entartete Matrix ist eine quadratische Matrix, die nicht invertiert werden kann und deren Determinante daher gleich 0 ist.

Um also zu wissen, wann eine Matrix singulär ist, berechnen Sie einfach ihre Determinante: Wenn das Ergebnis 0 ist, ist die Matrix singulär, wenn andererseits die Determinante von 0 verschieden ist, ist die Matrix nicht singulär .

Wenn Sie mehr über die inverse Matrix erfahren möchten, können Sie diese Seite konsultieren, auf der ausführlich erklärt wird , wie man eine Matrix mit der Gauß-Methode invertiert . Außerdem finden Sie mehrere Beispiele und Übungen, die Schritt für Schritt zum Üben gelöst werden.

Andererseits werden singuläre Matrizen auch als nichtreguläre Matrizen bezeichnet, da sie genau das Gegenteil von regulärer Matrix bedeuten.

Beispiele für singuläre Matrizen

Nachdem wir die Erklärung der singulären oder entarteten Matrix gesehen haben, sehen wir uns einige Beispiele für singuläre Matrizen mit mehreren Dimensionen an:

Beispiel einer 2×2-Singulärmatrix

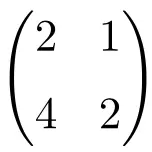
Beispiel einer singulären oder entarteten Matrix der Dimension 2x2

Wir können leicht überprüfen, dass es sich um eine singuläre Matrix handelt, indem wir ihre Determinante berechnen:

$\displaystyle\begin{vmatrix} 2&1 \\[1.1ex] 4 & 2\end{vmatrix}\bm{=0}$

Die Determinante der Matrix der Ordnung 2 ist gleich 0, es handelt sich also um eine singuläre Matrix.

Beispiel einer 3 × 3-Singulärmatrix

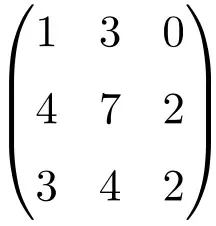
Beispiel einer singulären oder entarteten Matrix der Dimension 3x3

Wir müssen die Determinante der Matrix lösen, um zu überprüfen, ob es sich um eine nicht invertierbare Matrix handelt:

$\displaystyle\begin{vmatrix} 1&3&0\\[1.1ex] 4&7&2\\[1.1ex] 3&4&2\end{vmatrix}\bm{=0}$

Die Determinante der Matrix der Ordnung 3 ergibt 0, es handelt sich also um eine singuläre Matrix.

Beispiel einer 4 × 4-Singulärmatrix

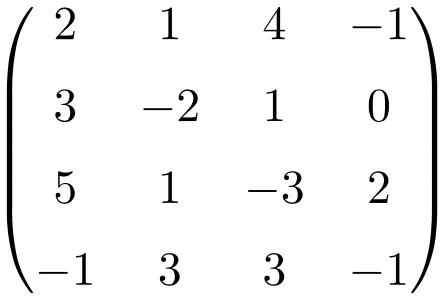
Beispiel einer singulären oder entarteten Matrix der Dimension 4x4

Indem wir die Determinante der Matrix bestimmen, zeigen wir, dass es sich um eine singuläre Matrix handelt:

$\displaystyle\begin{vmatrix} 2&1&4&-1\\[1.1ex] 3&-2&1&0\\[1.1ex] 5&1&-3&2\\[1.1ex] -1&3&3&-1\end{vmatrix}\bm{=0}$

Die Determinante der Matrix der Ordnung 4 ist Null, daher existiert ihre inverse Matrix nicht.

Warnung: Wenn Sie Zweifel an der Berechnung von Determinanten haben, können Sie die Seite zur Berechnung einer Determinante konsultieren.

Eigenschaften singulärer Matrizen

Die Merkmale dieser Art von Matrizen sind wie folgt:

Mindestens zwei Spalten oder zwei Zeilen einer singulären Matrix sind Linearkombinationen und daher linear abhängig.

Jede Matrix, die eine mit Nullen gefüllte Zeile oder Spalte enthält, ist eine singuläre Matrix.

Der Rang einer singulären oder entarteten Matrix ist kleiner als ihre Größe.

Das Matrixprodukt einer singulären Matrix multipliziert mit einer anderen Matrix ergibt eine weitere singuläre Matrix. Diese Bedingung lässt sich aus den Eigenschaften der Determinanten ableiten:

$\text{det}(AB) = \text{det}(A) \cdot \text{det}(B)=0 \cdot \text{det}(B) = 0$

Ebenso ist die Potenz einer singulären Matrix gleich der einer anderen singulären Matrix, unabhängig von der Potenz, auf die sie erhoben wird.

Die Transponierte einer singulären Matrix führt zu einer anderen singulären Matrix, da die Determinante einer transponierten (oder transponierten) Matrix äquivalent zur Determinante der nicht transponierten Matrix ist:

$\text{det}(A^t) = \text{det}(A)=0$

Die Multiplikation einer singulären Matrix mit einem Skalar ändert nichts an ihrem Status als entartete Matrix.

Der Adjunkt einer singulären Matrix ist ebenfalls singulär.

Dreiecksmatrizen und Diagonalmatrizen sind entartete Matrizen, wenn mindestens ein Element ihrer Hauptdiagonale Null ist.

Offensichtlich ist die Nullmatrix eine singuläre Matrix.

Ebenso ist eine nilpotente Matrix auch eine singuläre Matrix.

Ein System linearer Gleichungen, die einer singulären Matrix zugeordnet sind, hat keine Lösung oder unendlich viele Lösungen.

Schließlich ist eine quadratische Matrix genau dann singulär, wenn sie mindestens einen Eigenwert (oder Eigenwert) gleich 0 hat.

Singuläre oder entartete matrix