Hier erfahren Sie, wie die Tangensfunktion abgeleitet wird. Darüber hinaus können Sie Beispiele für die Ableitung des Tangens sehen und sogar mit Übungen üben, die Schritt für Schritt gelöst werden. Abschließend demonstrieren wir auch die Tangensableitungsformel und zeigen Ihnen die Umkehrtangensableitungsformel.
Was ist die Ableitung der Tangente?
Die Ableitung des Tangens von x ist gleich 1 über dem Quadrat des Kosinus von x. Die Ableitung des Tangens von x entspricht auch dem Quadrat der Sekante von x und 1 plus dem Quadrat des Tangens von x.
![Rendered by QuickLaTeX.com \begin{array}{c}f(x)=\text{tan}(x)\\[1.5ex]\color{orange}\bm{\downarrow}\color{black}\\ f'(x)=\cfrac{1}{\text{cos}^2(x)}=\text{sec}^2(x)=1+\text{tan}^2(x)\end{array}](https://mathority.org/wp-content/ql-cache/quicklatex.com-dfb81626a982a908c4e517b1ecb748e7_l3.png)
Alle Ausdrücke sind äquivalent, daher gibt es für die Tangensfunktion drei mögliche Formeln, um sie abzuleiten.
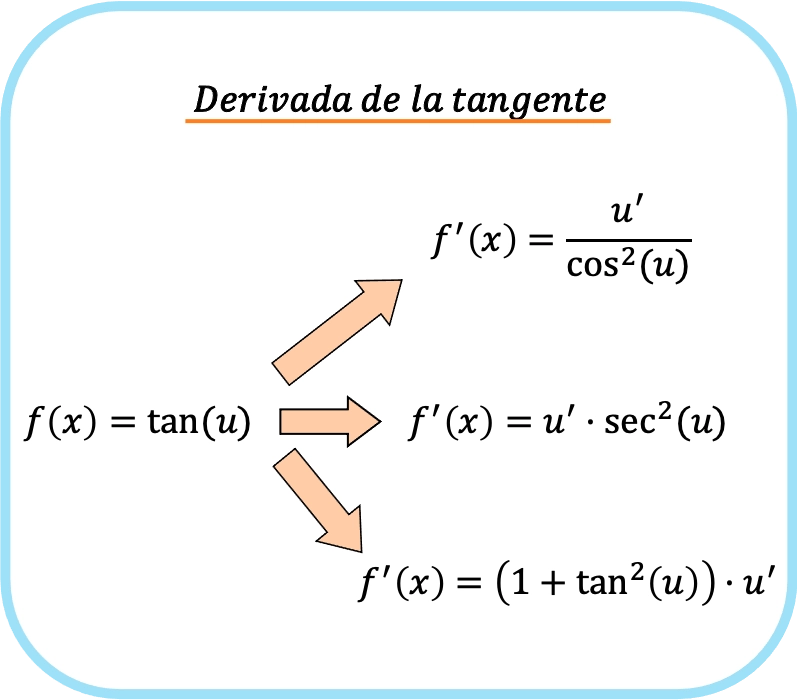
Wenn wir andererseits im Tangentenargument eine Funktion haben, die sich von x unterscheidet (nennen wir sie u), müssen wir die Kettenregel anwenden. Die Ableitung des Tangens von u ist daher:
![Rendered by QuickLaTeX.com \begin{array}{c}f(x)=\text{tan}(u)\\[1.5ex]\color{orange}\bm{\downarrow}\color{black}\\ f'(x)=\cfrac{u'}{\text{cos}^2(u)}=\text{sec}^2(u)\cdot u'=\left(1+\text{tan}^2(u)\right)\cdot u'\end{array}](https://mathority.org/wp-content/ql-cache/quicklatex.com-1ad272ab857ecf57ebc79e68a4370fc5_l3.png)
Kurz gesagt kann die Tangentenableitungsregel wie folgt zusammengefasst werden:
Beispiele für Tangentenableitungen
Angesichts der Formel für die Tangensableitung werden wir in diesem Abschnitt mehrere Beispiele dieser Art trigonometrischer Ableitungen lösen, damit Sie verstehen, wie Sie die Tangensfunktion ableiten.
Beispiel 1: Ableitung des Tangens von 2x
![]()
Um die Ableitung des Tangens zu berechnen, können Sie eine der drei Formeln verwenden, die wir oben gesehen haben. In diesem Fall verwenden wir die Kosinusformel:
![]()
Die Funktion 2x ist linear, daher ist ihre Ableitung 2. Die Ableitung des Tangens von 2x ist also 2 über dem Quadrat des Kosinus von 2x:
![]()
Beispiel 2: Ableitung des Tangens von x im Quadrat
![]()
In diesem Beispiel ist die Tangentenargumentfunktion kein x, sondern eine Funktion mit einer Ableitung. Das heißt, wir müssen die Kettenregel anwenden, um sie abzuleiten.
![]()
Die Ableitung von x im Quadrat ist 2x, also ist die Ableitung des Tangens von x 2 :
![]()
Beispiel 3: Ableitung der Tangente an den Würfel
![]()
In diesem Problem haben wir eine zusammengesetzte Funktion, daher müssen wir auch die Kettenregel verwenden, um den Tangens zu differenzieren.
![]()
Außerdem wird der Tangens mit 3 potenziert, was bedeutet, dass Sie vor der Anwendung der Formel für die Ableitung des Tangens die Formel für die Ableitung einer Potenz verwenden müssen:
![Rendered by QuickLaTeX.com \begin{aligned}f'(x)&=3\text{tan}^2(9x^2-4x)\cdot \cfrac{18x-4}{\text{cos}^2(9x^2-4x)} \\[2ex]&=\cfrac{3\text{tan}^2(9x^2-4x)\cdot(18x-4)}{\text{cos}^2(9x^2-4x)}\end{aligned}](https://mathority.org/wp-content/ql-cache/quicklatex.com-424a7372a1d97a5c17a86d6253666164_l3.png)
Ableitung des Umkehrtangens
Wie jede Umkehrfunktion hat auch die Tangensfunktion eine Umkehrfunktion, die Arkustangensfunktion. Obwohl die Formel zur Ableitung nicht der Tangensformel ähnelt, zeigen wir sie Ihnen, da sie in manchen Fällen nützlich sein kann.
Die Ableitung des Umkehrtangens einer Funktion ist der Quotient aus der Ableitung der Funktion dividiert durch eins plus dem Quadrat der Funktion
![]()
Die Ableitung des Umkehrtangens von 3x lautet beispielsweise:
![]()
Gelöste Übungen zur Ableitung des Tangens
Berechnen Sie die Ableitung der folgenden Tangensfunktionen:
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
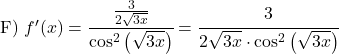
Beweis der Ableitung der Tangente
Damit Sie überprüfen können, dass es sich nicht um einen erfundenen Ausdruck handelt, demonstrieren wir in diesem Abschnitt die Formel für die Ableitung des Tangens anhand der mathematischen Definition des Tangens.
Dazu gehen wir von der trigonometrischen Identität aus, die die drei trigonometrischen Verhältnisse verbindet:
![]()
Wenn wir die Formel für die Ableitung einer Division verwenden, wäre die Ableitung:
![]()
![]()
![]()
Aber wenn wir die grundlegende trigonometrische Identität verwenden, wissen wir, dass das Quadrat des Sinus plus das Quadrat des Kosinus 1 ist:
![]()
![]()
Damit sind wir bereits bei der ersten Formel für die Ableitung des Tangens angelangt. Darüber hinaus ist die Sekante die multiplikative Umkehrung des Kosinus, sodass auch der zweite Ausdruck abgeleitet wird:
![]()
Schließlich kann die dritte Regel der Tangensableitung bewiesen werden, indem der Bruch aus dem vorherigen Schritt in eine Summe von Brüchen umgewandelt wird:
![]()
![]()
![]()