Faktorsatz - Mathematik

Auf dieser Seite erklären wir, was der Faktorsatz ist. Darüber hinaus zeigen wir, wofür der Faktorsatz verwendet wird: Teilbarkeit von Polynomen, Wurzeln finden, Polynome faktorisieren usw. Abschließend können Sie mit Schritt-für-Schritt-Übungen zum Faktorsatz üben.

Was ist der Faktorsatz?

In der Mathematik besagt der Faktorsatz , dass ein Polynom P(x) genau dann durch ein anderes Polynom der Form (xa) teilbar ist, wenn P(a)=0.

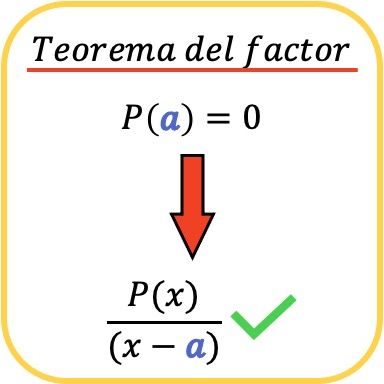
Ebenso folgt aus dem Faktorsatz, dass, wenn ein Polynom P(x) durch den Term (x−a) teilbar ist, dies bedeutet, dass der Wert a eine Wurzel (oder Null) des Polynoms P(x) ist ).

Dass ein Polynom durch ein anderes teilbar ist, bedeutet, dass der Rest (oder Rest) der Division zwischen den beiden Polynomen gleich Null ist. Falls Sie sich an dieses Konzept nicht vollständig erinnern, finden Sie unter dem folgenden Link Beispiele für die Division von Polynomen . Dort finden Sie auch eine Erklärung zur Division von Polynomen und Schritt für Schritt gelöste Übungen.

Beispiele für Faktorsätze

Nachdem wir nun die mathematische Definition des Faktorsatzes kennen, schauen wir uns einige Beispiele an, um zu sehen, wie er angewendet wird.

Beispiel 1

Eine Anwendung des Faktorsatzes besteht darin, herauszufinden, ob ein gegebenes Polynom durch ein Binomial teilbar ist. Sehen wir uns ein Beispiel an, wie dies mit dem Faktorsatz gemacht wird:

Bestimmen Sie, ob das Polynom P(x) durch das Binomial Q(x) teilbar ist, wobei beides gilt:

$P(x)=x^2-4x+3 \qquad \qquad Q(x)=x-1$

Erstens ist das Teilerpolynom Q(x) ein Polynom vom Typ (xa), sodass wir den Faktorsatz zur Lösung des Problems anwenden können.

Um also zu überprüfen, ob P(x) durch Q(x) geteilt werden kann, müssen wir den numerischen Wert des Polynoms P(x) für x=1 berechnen, da 1 der unabhängige Term des Divisionspolynoms mit geändertem Vorzeichen ist :

$\begin{aligned} P(1) & =1^2-4\cdot 1+3 \\[2ex] & = 1-4+3 \\[2ex] & = 0 \end{aligned}$

Der numerische Wert des Polynoms P(x) bei x = 1 ergibt Null, sodass P(x) gemäß dem Faktorsatz durch Q(x) teilbar ist, oder mit anderen Worten, der Rest der Division durch beide ist Null.

Wir können überprüfen, ob die Teilbarkeitsbedingung erfüllt ist, indem wir die beiden Polynome durch den Satz von Ruffini dividieren:

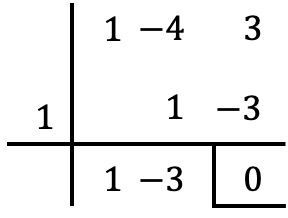
Wie Sie in diesem Beispiel sehen können, ist der Faktorsatz ein Sonderfall des Restsatzes (oder Restsatzes). Ich überlasse Ihnen diesen Artikel, der erklärt, was der Restsatz ist. Dort finden Sie auch Beispiele und damit gelöste Übungen. Und darüber hinaus können Sie den Unterschied zwischen dem Restsatz und dem Faktorsatz erkennen.

Beispiel 2

Der Faktorsatz kann auch verwendet werden, um die Nullstellen (oder Nullstellen) eines Polynoms zu finden. Aber um diese Art von Problem zu verstehen, muss man natürlich wissen , was die Wurzeln eines Polynoms sind . Wenn Sie dieses Konzept immer noch nicht verstehen, können Sie einen Blick auf die verlinkte Seite werfen, die ausführlich erklärt wird.

Sehen wir uns also anhand eines Beispiels an, wie der Faktorsatz angewendet wird, um eine Wurzel eines Polynoms zu finden:

Berechnen Sie anhand des Polynoms P(x), ob eine seiner Wurzeln x=2 ist:

$P(x)=x^3-3x^2+5x-6$

Bei Anwendung des Faktorsatzes ist der Term x=2 nur dann eine Wurzel des Polynoms P(x), wenn der numerische Wert von P(x) für x=2 Null ist. Wir müssen also diesen numerischen Wert finden:

$\begin{aligned} P(2) & =2^3-3\cdot 2^2+5\cdot 2-6 \\[2ex] & = 8-3\cdot 4 +5\cdot 2 -6\\[2ex] & = 8-12+10-6 \\[2ex] & = 0\end{aligned}$

Tatsächlich verschwindet der numerische Wert des Polynoms P(x) bei x=2, sodass wir dank des Faktorsatzes bestätigen können, dass x=2 eine Wurzel des Polynoms P(x) ist.

Faktorisieren von Polynomen mit dem Faktorsatz

Eine weitere Anwendung des Faktorsatzes ist die Faktorisierung von Polynomen . Falls Sie nicht wissen, was es ist: Das Faktorisieren eines Polynoms bedeutet, den Ausdruck eines Polynoms in ein Produkt von Faktoren umzuwandeln, d. h. das Faktorisieren eines Polynoms vereinfacht seinen algebraischen Ausdruck.

Somit legt der Fakultätssatz fest, dass, wenn ein Polynom P(x) P(a)=0 für einen gegebenen Wert a erfüllt, der Ausdruck dieses Polynoms in das Produkt P(x)=(xa)·Q( x), wobei Q(x) das Polynom ist, das sich aus der Division des Polynoms P(x) durch (xa) ergibt.

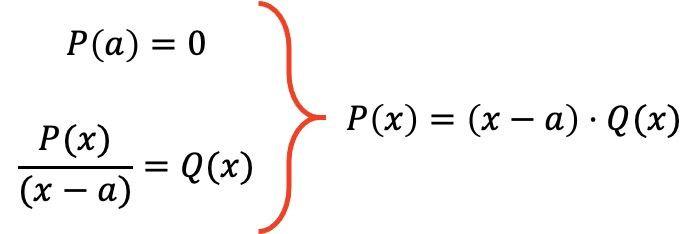
Als Beispiel werden wir das folgende Polynom mithilfe des Fakultätssatzes faktorisieren:

$P(x)=x^3+2x^2+4x+8$

Aus dem vorherigen Polynom können wir erkennen, dass x=-2 eine seiner Wurzeln ist, da der numerische Wert des Polynoms für x=-2 gleich Null ist:

$\begin{aligned} P(-2) & =(-2)^3+2\cdot (-2)^2+4\cdot (-2)+8 \\[2ex] & =-8+2\cdot 4+4\cdot (-2)+8 \\[2ex] & = -8+8-8+8 \\[2ex] & = 0 \end{aligned}$

Wir dividieren daher mit der Ruffini-Regel das Polynom P(x) zwischen dem durch x gebildeten Binomial und dieser Wurzel mit geändertem Vorzeichen, also dem Faktor (x+2):

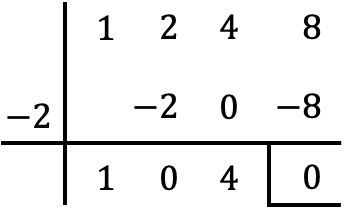
Der Quotient der Polynomdivision ist also:

$\cfrac{P(x)}{x+2} =x^2+4$

Und schließlich können wir aus dem Faktorsatz das Polynom P(x) in Form einer Multiplikation des Faktors (x+2) mit dem in der vorherigen Division erhaltenen Quotienten ausdrücken:

$P(x) = (x+2) \cdot (x^2+4)$

Damit haben wir das Polynom P(x) faktorisiert, allerdings nur teilweise. Um ein Polynom vollständig zu faktorisieren, muss ein längeres Verfahren angewendet werden. Wir haben eine Anleitung erstellt, in der wir Schritt für Schritt zeigen , wie man Ruffini-Polynome faktorisiert . Darüber hinaus haben wir in diesem Artikel alle Arten der Faktorisierung erklärt und Sie können mit gelösten Übungen üben. Klicken Sie also auf den Link, um herauszufinden, wie Sie ein Polynom aus der Menge faktorisieren.

Probleme mit dem Faktorsatz gelöst

Anschließend haben wir mehrere Übungen vorbereitet, die Schritt für Schritt zum Faktorsatz gelöst werden, damit Sie üben und so überprüfen können, ob Sie diesen Satz verstanden haben. Wir empfehlen Ihnen, diese selbst auszuprobieren und dann zu prüfen, ob Sie die Lösung richtig verstehen. Vergessen Sie auch nicht, dass Sie uns Ihre Fragen unten in den Kommentaren hinterlassen können! ❓❓💬💬

Übung 1

Verwenden Sie den Fakultätssatz, um herauszufinden, ob das Polynom P(x) durch das Binomial Q(x) teilbar ist. Wenn ja, ermitteln Sie eine Wurzel des Polynoms und faktorisieren Sie diese.

$P(x)=2x^3-4x^2+x-7 \qquad \qquad Q(x)=x-3$

siehe Lösung

In diesem Fall ist der Polynomteiler Q(x) ein Binomial, das nur aus einem x und einem unabhängigen Term besteht. Um zu zeigen, dass das Polynom P(x) mit dem Fakultätssatz durch das andere Polynom Q(x) geteilt werden kann, müssen wir den numerischen Wert des Polynoms P(x) im unabhängigen Term des Divisorpolynoms mit geändertem Vorzeichen auswerten. das heißt bei x=3:

$\begin{aligned} P(3) & =2\cdot 3^3-4\cdot 3^2+3-7\\[2ex] & = 2\cdot 27-4\cdot 9+3-7 \\[2ex] & = 54-36+3-7\\[2ex] & = 14 \end{aligned}$

Der Zahlenwert des Polynoms P(x) bei x=3 entspricht 14, ist also von Null verschieden. Nach dem Faktorsatz ist P(x) also NICHT durch Q(x) teilbar, da der Rest der Division nicht Null ist.

Übung 2

Finden Sie mithilfe des Fakultätssatzes heraus, ob das Polynom P(x) durch das Binomial Q(x) teilbar ist. Wenn ja, ermitteln Sie eine Wurzel des Polynoms P(x) und faktorisieren Sie diese.

$P(x)=x^3+5x^2+3x-1 \qquad \qquad Q(x)=x+1$

siehe Lösung

In diesem Fall ist der Polynomteiler Q(x) ein Binomial, das nur aus einem x und einem unabhängigen Term besteht, wir können daher den Fakultätssatz anwenden.

Und um zu überprüfen, ob das Polynom P(x) durch das Polynom Q(x) geteilt werden kann, müssen wir den numerischen Wert des Polynoms P(x) für den unabhängigen Term des Polynoms Q(x) mit geändertem Vorzeichen ermitteln dh bei x=-1:

$\begin{aligned} P(-1) & =(-1)^3+5\cdot (-1)^2+3\cdot (-1)-1\\[2ex] & = -1+5\cdot 1+3\cdot (-1)-1\\[2ex] & = -1+5-3-1\\[2ex] & = 0 \end{aligned}$

In diesem Problem ist der numerische Wert des Polynoms bei x=-1 Null, sodass P(x) durch Q(x) teilbar ist.

Dann können wir durch den Fakultätssatz ableiten, dass x=-1 eine Wurzel des Polynoms P(x) ist, da der numerische Wert von P(x) bei x=-1 verschwindet.

Da also x=-1 eine Wurzel des Polynoms P(x) ist, teilen Sie es zum Faktorisieren einfach durch x+1. Und dazu verwenden wir die Ruffini-Methode:

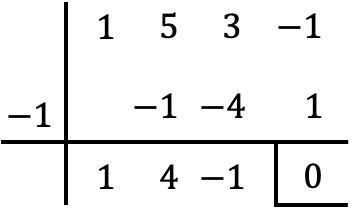
Das Ergebnis der Operation ist also:

$x^2+4x-1$

Wir können das Polynom P(x) daher wie folgt faktorisieren:

$P(x) = (x+1) \cdot (x^2+4x-1)$

Übung 3

Finden Sie mit dem Fakultätssatz heraus, ob das Polynom P(x) durch das Binomial Q(x) teilbar ist, und wenn ja, finden Sie auch eine Wurzel des Polynoms P(x) und faktorisieren Sie diese.

$P(x)=x^3+5x^2+4x-6 \qquad \qquad Q(x)=x+3$

siehe Lösung

In diesem Fall ist das Polynom, das Q(x) teilt, ein Binomial, das nur aus einem x und einem unabhängigen Term besteht, sodass wir den Faktorsatz verwenden können.

Und um zu überprüfen, ob das Polynom P(x) durch das Polynom Q(x) teilbar ist, müssen wir den numerischen Wert des Polynoms P(x) für den unabhängigen Term des Polynoms Q(x) mit geändertem Vorzeichen bestimmen, d. h. d.h. bei x =-3:

$\begin{aligned} P(-3) & =(-3)^3+5\cdot (-3)^2+4\cdot (-3)-6\\[2ex] & = -27+5\cdot 9+4\cdot (-3)-6\\[2ex] & = -27+45-12-6\\[2ex] & = 0 \end{aligned}$

In diesem Fall ist der numerische Wert des Polynoms bei x=-3 Null, sodass P(x) tatsächlich durch Q(x) teilbar ist.

Aus diesem Grund folgern wir aus dem Fakultätssatz, dass x=-3 eine Wurzel des Polynoms P(x) ist, da P(-3) gleich Null ist.

Da also x=-3 eine Wurzel des Polynoms P(x) ist, müssen wir es zum Faktorisieren durch x+3 dividieren. Und dazu verwenden wir Ruffinis Regel:

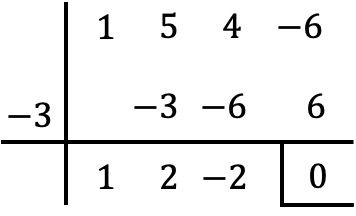
Das Ergebnis der Division ist also:

$x^2+2x-2$

Und deshalb können wir das Polynom P(x) wie folgt faktorisieren:

$P(x) = (x+3) \cdot (x^2+2x-2)$

Was halten Sie vom Faktorsatz? Glauben Sie, dass es in der Algebra nützlich ist? Wir haben Sie in den Kommentaren gelesen!
👀⬇⬇⬇👀

Was ist der Faktorsatz?

Beispiele für Faktorsätze

Beispiel 1

Beispiel 2

Faktorisieren von Polynomen mit dem Faktorsatz

Probleme mit dem Faktorsatz gelöst

Übung 1

Übung 2

Übung 3

Kommentar verfassen Kommentieren abbrechen