Diese Seite ist sicherlich die umfassendste Erklärung der Hessischen Matrix, die es gibt. Hier wird das Konzept der Hesse-Matrix erklärt, wie man sie anhand von Beispielen berechnet und es gibt sogar mehrere gelöste Übungen zum Üben. Darüber hinaus erfahren Sie, wie die Maximal- und Minimalwerte einer multivariablen Funktion berechnet werden und ob es sich um eine konkave oder konvexe Funktion handelt. Und schließlich finden Sie dort auch die Dienstprogramme und Anwendungen der hessischen Matrix.
Was ist die Hessische Matrix?
Die Definition der hessischen (oder hessischen) Matrix lautet wie folgt:
Die Hesse-Matrix ist eine quadratische Matrix der Dimension n × n, die aus den partiellen zweiten Ableitungen einer Funktion von n Variablen besteht.
Diese Matrix ist auch als Hessische Matrix bekannt, oder in einigen Mathematikbüchern wird sie sogar als Diskriminante bezeichnet. Die gebräuchlichste Bezeichnung dafür ist jedoch die Hesse-Matrix.
Die Formel für die Hesse-Matrix lautet daher wie folgt:

Daher ist die Hesse-Matrix immer eine quadratische Matrix, deren Dimension gleich der Anzahl der Variablen in der Funktion ist. Wenn die Funktion beispielsweise drei Variablen hat, hat die Hesse-Matrix die Dimension 3×3.
Darüber hinaus besagt der Satz von Schwarz (oder der Satz von Clairaut), dass die Reihenfolge der Differenzierung keine Rolle spielt, dh teilweise zuerst in Bezug auf die Variable ableiten
![]()
dann in Bezug auf die Variable
![]()
kommt einer teilweisen Differenzierung in Bezug auf gleich
![]()
dann Respekt
![]()
.
![]()
Daher ist die Hesse-Matrix eine symmetrische Matrix, oder mit anderen Worten, sie hat eine Symmetrie, deren Achse ihre Hauptdiagonale ist.
Kurioserweise ist die Hessische Matrix nach Ludwig Otto Hesse benannt, einem deutschen Mathematiker des 19. Jahrhunderts, der sehr wichtige Beiträge auf dem Gebiet der linearen Algebra leistete.
Beispiel für die Berechnung der Hessischen Matrix
Sehen wir uns ein Beispiel an, wie man eine Hesse-Matrix mit der Dimension 2 × 2 findet:
- Berechnen Sie die Hesse-Matrix am Punkt (1,0) der folgenden Funktion:
![]()
Zuerst müssen wir die partiellen Ableitungen erster Ordnung berechnen:
![]()
![]()
Sobald wir die ersten Ableitungen bereits kennen, berechnen wir alle partiellen Ableitungen zweiter Ordnung:
![]()
![]()
![]()
Daher können wir nun die Hesse-Matrix aus der Formel für 2 × 2-Matrizen ermitteln:
![Rendered by QuickLaTeX.com \displaystyle H_f (x,y)=\begin{pmatrix}\cfrac{\partial^2 f}{\partial x^2} & \cfrac{\partial^2 f}{\partial x \partial y} \\[4ex] \cfrac{\partial^2 f}{\partial y \partial x} & \cfrac{\partial^2 f}{\partial y^2} \end{pmatrix}](https://mathority.org/wp-content/ql-cache/quicklatex.com-926f350fe0ac3184ec0b563b57fd6041_l3.png)
![Rendered by QuickLaTeX.com \displaystyle H_f (x,y)=\begin{pmatrix}6x +6 &-4 \\[2ex] -4 & 12y^2+8 \end{pmatrix}](https://mathority.org/wp-content/ql-cache/quicklatex.com-b7f3d45918645a5b6019896ed45eda75_l3.png)
Somit lautet die am Punkt (1,0) ausgewertete Hesse-Matrix:
![Rendered by QuickLaTeX.com \displaystyle H_f (1,0)=\begin{pmatrix}6(1) +6 &-4 \\[2ex] -4 & 12(0)^2+8 \end{pmatrix}](https://mathority.org/wp-content/ql-cache/quicklatex.com-bdccfc61f7befe6c75f66c8a4658f3e6_l3.png)
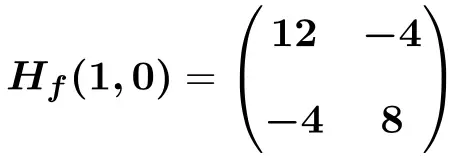
Probleme mit hessischen Matrizen gelöst
Übung 1
Berechnen Sie die Hesse-Matrix der folgenden Funktion mit 2 Variablen am Punkt (1,1):
![]()
Zuerst müssen wir die partiellen Ableitungen erster Ordnung der Funktion finden:
![]()
![]()
Nachdem wir bereits die ersten Ableitungen berechnet haben, fahren wir mit der Lösung aller partiellen Ableitungen zweiter Ordnung fort:
![]()
![]()
![]()
Somit ist die Hesse-Matrix wie folgt definiert:
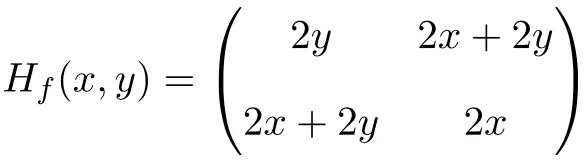
Abschließend bleibt nur noch die Auswertung der Hesse-Matrix bei Punkt (1,1):
![Rendered by QuickLaTeX.com \displaystyle H_f (1,1)=\begin{pmatrix}2\cdot 1 &2 \cdot 1+2\cdot 1 \\[1.5ex] 2\cdot 1+2\cdot 1 & 2\cdot 1 \end{pmatrix}](https://mathority.org/wp-content/ql-cache/quicklatex.com-e5353c0229942269e07455047284f92b_l3.png)
![Rendered by QuickLaTeX.com \displaystyle \bm{H_f (1,1)}=\begin{pmatrix}\bm{2} & \bm{4} \\[1.1ex] \bm{4} & \bm{2} \end{pmatrix}](https://mathority.org/wp-content/ql-cache/quicklatex.com-cf00fccdb37a19388e76b5a84a408d02_l3.png)
Übung 2
Berechnen Sie den Hesse-Wert am Punkt (1,1) der folgenden Funktion in zwei Variablen:
![]()
Zuerst müssen wir die partiellen Ableitungen erster Ordnung der Funktion berechnen:
![]()
![]()
Sobald wir die ersten Ableitungen haben, berechnen wir die partiellen Ableitungen zweiter Ordnung der Funktion:
![]()
![]()
![]()
Somit ist die Hesse-Matrix der Funktion eine quadratische Matrix der Dimension 2×2:
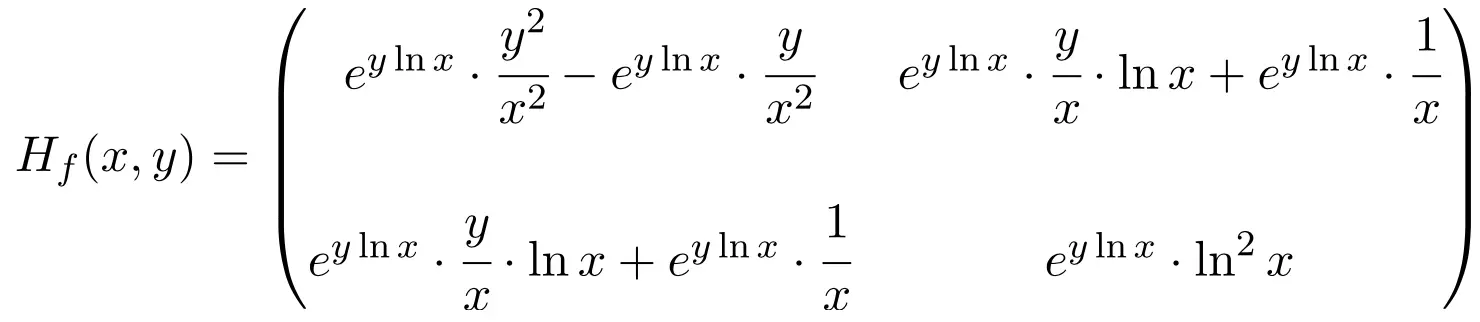
Abschließend bleibt nur noch die Auswertung der Hesse-Matrix bei Punkt (1,1):
![Rendered by QuickLaTeX.com \displaystyle H_f (1,1)=\begin{pmatrix} e^{1\ln (1)} \displaystyle \cdot \cfrac{1^2}{1^2} - e^{1\ln (1)} \cdot \cfrac{1}{1^2}& e^{1\ln (1)} \cdot \cfrac{1}{1}\cdot \ln (1) + e^{1\ln (1)}\cdot \cfrac{1}{1} \\[3ex] e^{1\ln (1)} \cdot \cfrac{1}{1}\cdot \ln (1) + e^{1\ln (1)}\cdot \cfrac{1}{1} & e^{1\ln (1)} \cdot \ln ^2 (1) \end{pmatrix}](https://mathority.org/wp-content/ql-cache/quicklatex.com-c316cc61e6d007e5d034274e0f494520_l3.png)
![Rendered by QuickLaTeX.com \displaystyle H_f (1,1)=\begin{pmatrix}e^{0} \cdot 1 - e^{0} \cdot 1& e^{0} \cdot 1\cdot 0 + e^{0}\cdot 1 \\[2ex] e^{0} \cdot 1\cdot 0 + e^{0}\cdot 1 & e^{0} \cdot 0\end{pmatrix}](https://mathority.org/wp-content/ql-cache/quicklatex.com-6e456b856c722a140d73ade63f13ec9f_l3.png)
![Rendered by QuickLaTeX.com \displaystyle H_f (1,1)=\begin{pmatrix}1 - 1& 0+ 1 \\[1.5ex] 0 +1 & 1 \cdot 0\end{pmatrix}](https://mathority.org/wp-content/ql-cache/quicklatex.com-929fbf6e7f0f90110d11d4ccd51fd51a_l3.png)
![Rendered by QuickLaTeX.com \displaystyle \bm{H_f (1,1)}=\begin{pmatrix}\bm{0} & \bm{1} \\[1.1ex] \bm{1} & \bm{0} \end{pmatrix}](https://mathority.org/wp-content/ql-cache/quicklatex.com-ce780ddb8c09515afccfb2da2d842584_l3.png)
Übung 3
Finden Sie die Hesse-Matrix an diesem Punkt
![]()
der folgenden Funktion mit 3 Variablen:
![]()
Zuerst berechnen wir die partiellen Ableitungen erster Ordnung der Funktion:
![]()
![]()
![]()
Sobald wir die ersten Ableitungen haben, berechnen wir die partiellen Ableitungen zweiter Ordnung der Funktion:
![]()
![]()
![]()
![]()
![]()
![]()
Damit ist die Hesse-Matrix der Funktion eine quadratische Matrix der Dimension 3×3:
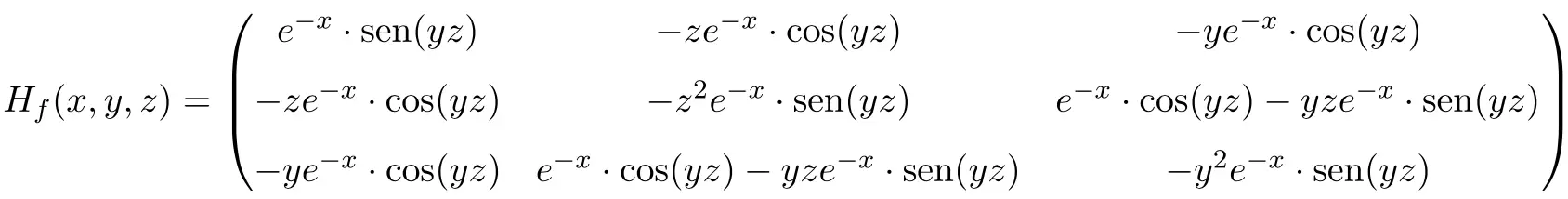
Abschließend ersetzen wir die Variablen durch ihre jeweiligen Werte an der Stelle
![]()
![Rendered by QuickLaTeX.com \displaystyle H_f(0,1,\pi)=\begin{pmatrix}e^{-0}\cdot \text{sen}(1\pi) & -\pi e^{-0}\cdot \text{cos}(1\pi) &-1e^{-0}\cdot \text{cos}(1\pi) \\[1.5ex] -\pi e^{-0}\cdot \text{cos}(1 \pi)&-\pi^2e^{-0}\cdot \text{sen}(1 \pi) &e^{-0}\cdot \text{cos}(1 \pi)-1 \pi e^{-0}\cdot \text{sen}(1 \pi) \\[1.5ex] -1e^{-0}\cdot \text{cos}(1 \pi)& e^{-0}\cdot \text{cos}(1 \pi)-1 \pi e^{-0}\cdot \text{sen}(1 \pi)& -1^2e^{-0}\cdot \text{sen}(1 \pi) \end{pmatrix}](https://mathority.org/wp-content/ql-cache/quicklatex.com-4e198192f67babd81228caa53b66e8a0_l3.png)
![Rendered by QuickLaTeX.com \displaystyle H_f(0,1,\pi)=\begin{pmatrix}1\cdot 0 & -\pi \cdot 1 \cdot (-1)&-1\cdot 1 \cdot (-1) \\[1.5ex] -\pi \cdot 1 \cdot (-1) &-\pi^2\cdot 1\cdot 0 &1 \cdot (-1)-\pi \cdot 1\cdot 0 \\[1.5ex] -1\cdot 1 \cdot (-1) & 1\cdot (-1) - \pi \cdot 1\cdot 0 & -1\cdot 1 \cdot 0 \end{pmatrix}](https://mathority.org/wp-content/ql-cache/quicklatex.com-4ce9c6b4cfcddfb0c2eb51db1189c653_l3.png)
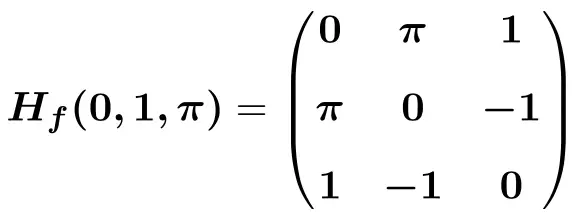
Übung 4
Bestimmen Sie die Hesse-Matrix am Punkt (2,-1,1,-1) der folgenden Funktion mit 4 Variablen:
![]()
Der erste Schritt besteht darin, die partiellen Ableitungen erster Ordnung der Funktion zu finden:
![]()
![]()
![]()
![]()
Nun lösen wir die partiellen Ableitungen zweiter Ordnung der Funktion:
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
Somit ist der Ausdruck der 4×4-Hesse-Matrix, die durch Lösen aller partiellen Ableitungen erhalten wird, der folgende:
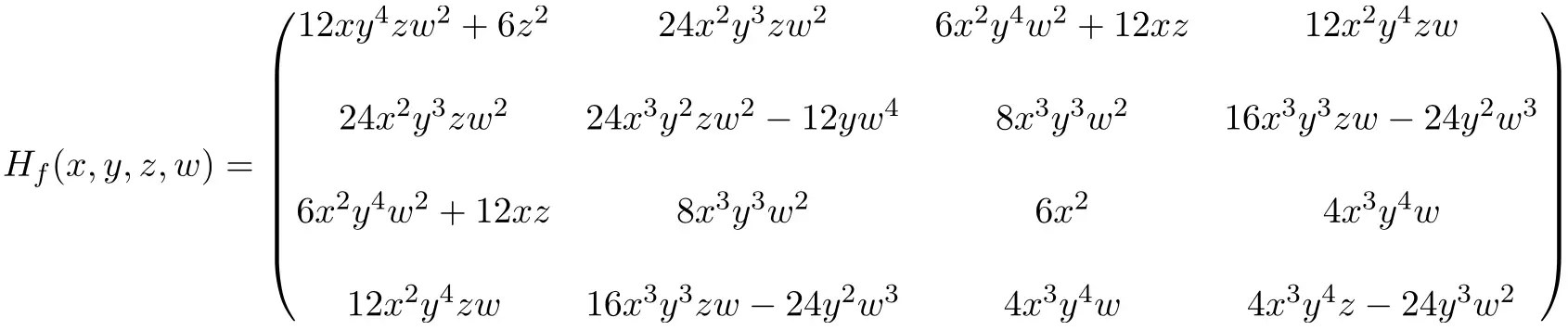
Schließlich ersetzen wir die Unbekannten durch ihre jeweiligen Punktwerte (2,-1,1,-1) und führen die Berechnungen durch:
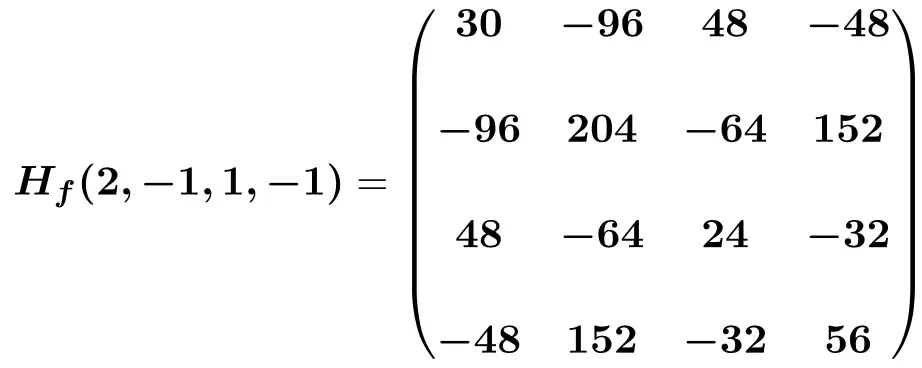
Woher wissen Sie, wann die Hesse-Matrix positiv, negativ oder unbestimmt ist?
Wie wir später sehen werden, ist es sehr nützlich zu wissen, ob die Hessische Matrix eine positiv semidefinite, positiv definite, negative semidefinite, negativ definite oder unbestimmte Matrix ist. Mal sehen, wie wir das herausfinden können:
Kriterium der Eigenwerte (oder Eigenwerte)
Eine Möglichkeit herauszufinden, um welche Art von Matrix es sich handelt, besteht darin, die Eigenwerte (oder Eigenwerte) der Hesse-Matrix durchzugehen:
- Die Hesse-Matrix ist positiv semidefinit, wenn sie Eigenwerte (oder Eigenwerte) gleich und größer als Null aufweist. Das heißt, es hat positive Eigenwerte und mindestens einen gleich 0:
![]()
- Die Hesse-Matrix ist positiv definit , wenn alle ihre Eigenwerte (oder Eigenwerte) ausschließlich größer als 0 (positiv) sind:
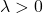 negativ semidefinit, wenn sie Eigenwerte (oder Eigenwerte) gleich und kleiner als Null hat. Das heißt, es hat negative Eigenwerte und mindestens einen gleich 0:
negativ semidefinit, wenn sie Eigenwerte (oder Eigenwerte) gleich und kleiner als Null hat. Das heißt, es hat negative Eigenwerte und mindestens einen gleich 0:
![]()
- Die Hesse-Matrix ist negativ definit , wenn alle ihre Eigenwerte (oder Eigenwerte) kleiner als 0 (negativ) sind:
![]()
- Die Hesse-Matrix ist undefiniert , wenn sie positive und negative Eigenwerte (oder Eigenwerte) hat:
![]()
Sylvester-Kriterium
Eine andere Möglichkeit herauszufinden, um welchen Typ es sich bei der Hessischen Matrix handelt, ist die Verwendung des Sylvester-Kriteriums. Dieser Satz lässt uns jedoch nur wissen, ob sie positiv definit, negativ definit oder unbestimmt ist. Aber manchmal kann die Verwendung viel schneller sein, da die Berechnungen im Allgemeinen einfacher sind.
Somit lautet das Sylvester-Kriterium wie folgt:
- Wenn alle Hauptminorwerte der Hesse-Matrix größer als 0 sind, handelt es sich um eine positiv definite Matrix.
- Wenn die Hauptminorwerte der Hesse-Matrix mit geradem Index größer als 0 und diejenigen mit ungeradem Index kleiner als 0 sind, handelt es sich um eine negativ definite Matrix.
- Wenn alle Hauptminorwerte der hessischen Matrix ungleich 0 sind und keine der beiden vorherigen Bedingungen erfüllt ist, handelt es sich um eine unbestimmte Matrix.
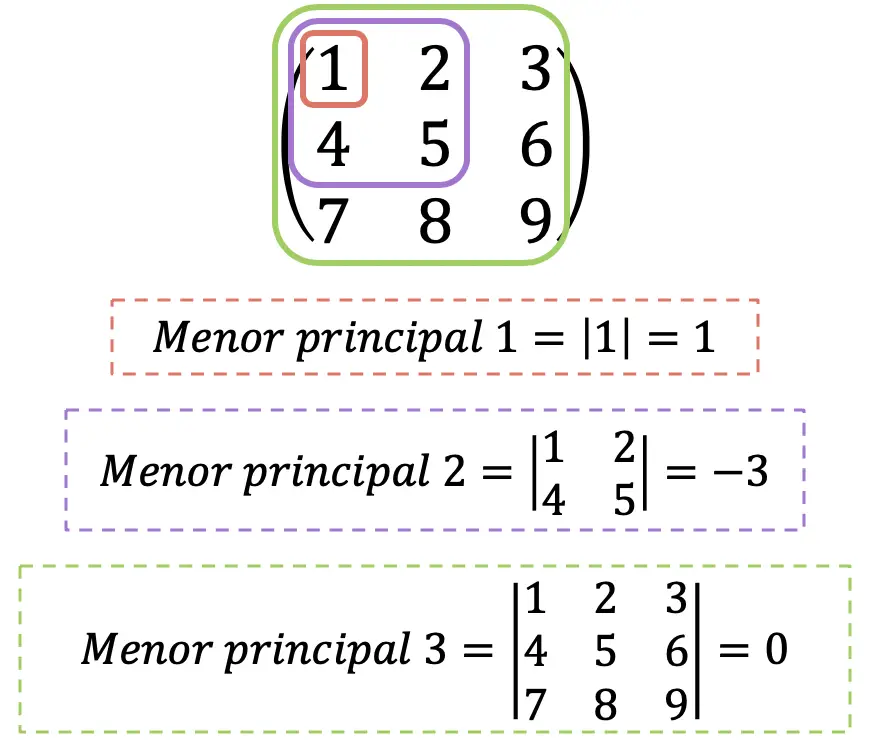
Offensichtlich fällt das maximale Haupt-Moll der Hesse-Matrix immer mit seiner Determinante zusammen. Nur zu Informationszwecken wird die Determinante der Hesse-Matrix auch „die Hesse-Matrix“ genannt, obwohl wir dies hier nicht tun, um Verwirrung zu vermeiden.
So berechnen Sie ein Maximum oder Minimum einer Funktion mit der Hesse-Matrix
Sobald Sie wissen, wie man die Hesse-Matrix berechnet, fragen Sie sich wahrscheinlich: Und wofür wird diese Matrix verwendet?
Nun, eine der Anwendungen der Hessischen Matrix besteht darin, das Maximum oder Minimum einer Funktion mit mehr als einer Variablen zu finden. Hier finden Sie eine Schritt-für-Schritt-Erklärung zur Berechnung von Maxima und Minima:
- Zunächst werden die kritischen Punkte der multivariablen Funktion berechnet. Dazu berechnen wir den Gradienten bzw. die Jacobi-Matrix der Funktion, setzen diese gleich 0 und lösen die Gleichungen.
- Die hessische Matrix wird berechnet.
- Die in Schritt 1 gefundenen kritischen Punkte werden in die Hesse-Matrix eingesetzt. Wir erhalten somit so viele Hesse-Matrizen, wie kritische Punkte die Funktion haben.
- Wir schauen uns an, um welchen Matrixtyp es sich bei jeder hessischen Matrix handelt. Das heißt, wir schauen, ob es positiv definit, negativ definit, unbestimmt usw. ist.
- Wenn die Hesse-Matrix positiv definit ist, ist der kritische Punkt ein relatives Minimum der Funktion.
- Wenn die Hesse-Matrix negativ definit ist, ist der kritische Punkt ein relatives Maximum der Funktion.
- Wenn die Hesse-Matrix undefiniert ist, ist der kritische Punkt ein Sattelpunkt .
Beispiel für die Berechnung von Maxima und Minima einer multivariablen Funktion
Um zu sehen, wie dies geschieht, finden Sie hier ein Beispiel für die Berechnung und Klassifizierung der relativen Extrema einer Funktion mithilfe der Hesse-Matrix:
- Finden Sie alle relativen Extrema der folgenden multivariablen Funktion:
![]()
Als Erstes müssen wir die Jacobi-Matrix der Funktion berechnen, die in diesem Fall mit dem Gradienten übereinstimmt, da es sich um eine Skalarfunktion handelt:
![]()
Wir müssen nun die kritischen Punkte bestimmen, dazu gleichen wir die erhaltenen Gleichungen auf 0 aus und lösen das Gleichungssystem:
![]()
![Rendered by QuickLaTeX.com \displaystyle \left. \begin{array}{l} 2x+2y+4 =0 \\[2ex] -2y+2x-4=0 \end{array}\right\} \longrightarrow \left. \begin{array}{c} x = 0 \\[1.1ex] y = -2 \end{array}\right\} \longrightarrow \ (0,-2)](https://mathority.org/wp-content/ql-cache/quicklatex.com-d851eb626a9bd385aec8f68c9df71a39_l3.png)
Der kritische Punkt, den wir gefunden haben, ist also (0,-2).
Nachdem der kritische Punkt der Funktion gefunden wurde, müssen wir die Hessesche Matrix berechnen:
![Rendered by QuickLaTeX.com \displaystyle H_f (x,y)=\begin{pmatrix}2 & 2 \\[1.1ex] 2 & -2 \end{pmatrix}](https://mathority.org/wp-content/ql-cache/quicklatex.com-702fa5f5c3e3d872e1ec0dad0e3216c7_l3.png)
Und natürlich ist die am kritischen Punkt ausgewertete Hesse-Matrix dieselbe:
![Rendered by QuickLaTeX.com \displaystyle H_f (0,-2)=\begin{pmatrix}2 & 2 \\[1.1ex] 2 & -2 \end{pmatrix}](https://mathority.org/wp-content/ql-cache/quicklatex.com-7b56ffff28d1a9b98c9848891ae924eb_l3.png)
Um zu sehen, um welche Art von Matrix es sich handelt, verwenden wir das Sylvester-Kriterium. Wir lösen daher die Hauptminorwerte der Matrix:
![]()
![Rendered by QuickLaTeX.com \displaystyle \begin{vmatrix}2 & 2 \\[1.1ex] 2 & -2 \end{vmatrix} = -8](https://mathority.org/wp-content/ql-cache/quicklatex.com-d66efe9fca481475009bb1703939e4f6_l3.png)
Haupt-Nebenzahl 1 (ungerade) ist positiv und Haupt-Nebenzahl 2 (gerade) ist negativ, sodass es sich nach Sylvesters Kriterium um eine unbestimmte Matrix handelt. Und daher ist der kritische Punkt (0,-2) ein Sattelpunkt.
Bestimmen der Konkavität oder Konvexität einer Funktion mit der Hesseschen Matrix
Eine andere Verwendung der Hesse-Matrix besteht darin, zu wissen, ob eine Funktion konkav oder konvex ist. Und dies lässt sich nach folgendem Satz ermitteln:
Sei
![]()
eine offene Menge und
![]()
eine Funktion, deren zweite Ableitungen stetig sind, ihre Konkavität und Konvexität werden durch die Hesse-Matrix definiert:
- Funktion

ist durchgehend konvex

genau dann, wenn ihre Hesse-Matrix an jedem Punkt der Menge positiv semidefinit ist.
- Funktion

ist durchgehend streng konvex

genau dann, wenn ihre Hesse-Matrix an jedem Punkt der Menge positiv definit ist.
✓ Daher, wenn
![]()
ist eine konvexe Funktion an einem Punkt, an dem auch die Jacobi-Matrix verschwindet. Dieser Punkt ist ein lokales Minimum .
- Funktion

ist insgesamt konkav

genau dann, wenn ihre Hesse-Matrix an jedem Punkt der Menge negativ semidefinit ist.
- Funktion

ist insgesamt streng konkav

genau dann, wenn ihre Hesse-Matrix an jedem Punkt der Menge negativ definit ist.
✓ Daher, wenn
![]()
ist eine Funktion, die an einem Punkt konkav ist, an dem auch die Jacobi-Matrix verschwindet. Dieser Punkt ist ein lokales Maximum .
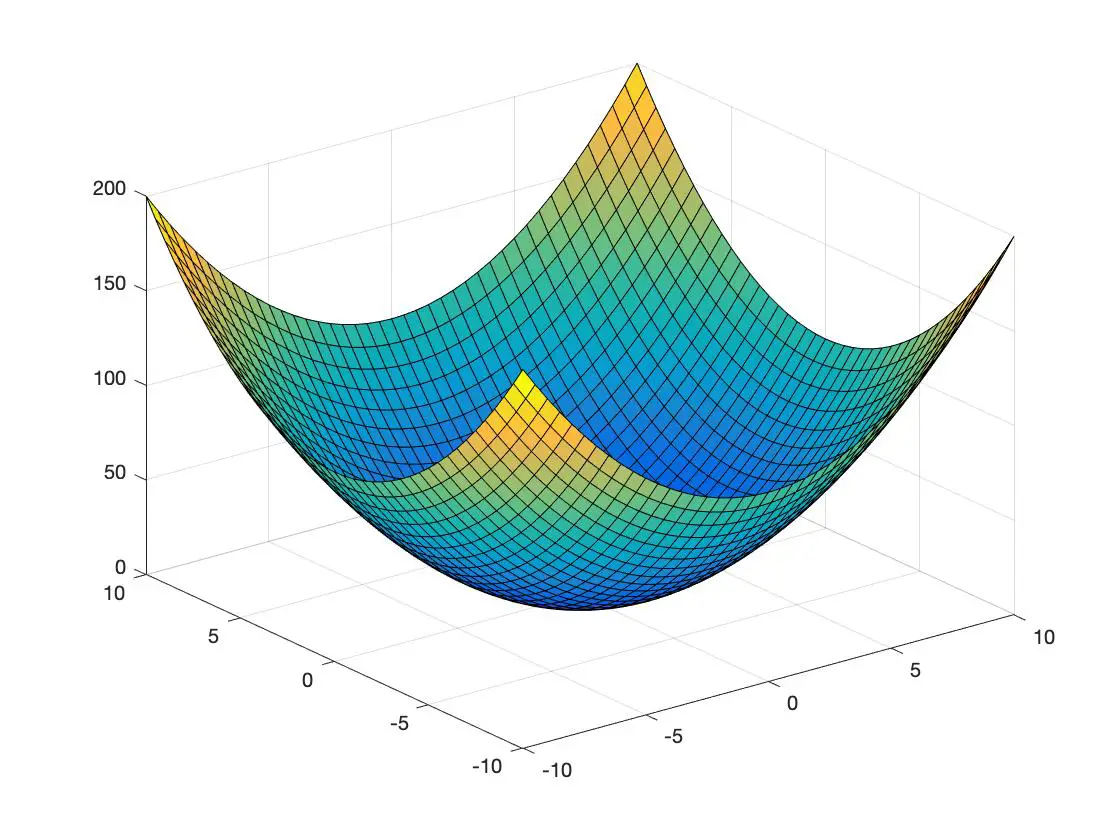
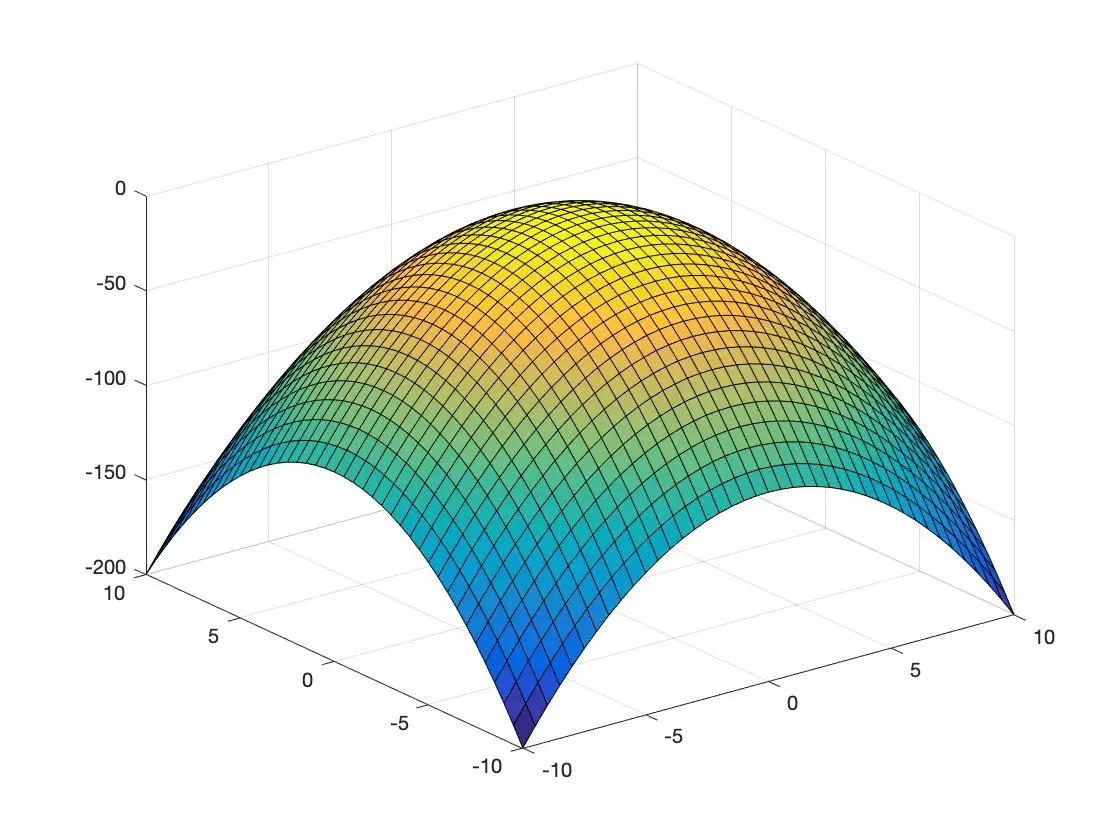
Unten sehen Sie ein Beispiel für eine konvexe Funktion und ein weiteres für eine konkave Funktion, dargestellt in einem dreidimensionalen Raum:
konvexe Funktion
konkave Funktion
Weitere Anwendungen der Hessischen Matrix
Die Hauptverwendungen der Hesse-Matrix sind die, die wir bereits gesehen haben, sie hat jedoch auch andere Anwendungen. Wir erklären sie unten für die Neugierigsten.
Taylor-Polynom
Die Entwicklung des Taylor-Polynoms für Funktionen von zwei oder mehr Variablen am Punkt
![]()
fängt so an:
![]()
Wie Sie sehen können, sind die Terme zweiter Ordnung der Taylor-Entwicklung durch die Hesse-Matrix gegeben, die am Punkt der Entwicklung des Polynoms ausgewertet wird.
Umrandete Sackleinen-Matrix
Eine weitere Verwendung der Hesse-Matrix besteht darin, die Minima und Maxima einer multivariaten Funktion zu berechnen
![]()
auf eine andere Rolle beschränkt
![]()
. Um dieses Problem zu lösen, wird die begrenzte Hesse-Matrix verwendet und wie folgt vorgegangen:
Schritt 1: Die Lagrange-Funktion wird berechnet, die durch den folgenden Ausdruck definiert ist:
![]()
Schritt 2: Die kritischen Punkte der Lagrange-Funktion werden gefunden. Dazu berechnen wir die Steigung der Lagrange-Funktion, setzen die Gleichungen gleich 0 und lösen die Gleichungen.
![]()
![]()
Schritt 3: Für jeden gefundenen Punkt berechnen wir den begrenzten Hesse-Wert, der durch die folgende Matrix definiert ist:
![Rendered by QuickLaTeX.com \displaystyle H(f,g) = \begin{pmatrix}0 & \cfrac{\partial g}{\partial x_1} & \cfrac{\partial g}{\partial x_2} & \cdots & \cfrac{\partial g}{\partial x_n} \\[4ex] \cfrac{\partial g}{\partial x_1} & \cfrac{\partial^2 f}{\partial x_1^2} & \cfrac{\partial^2 f}{\partial x_1\,\partial x_2} & \cdots & \cfrac{\partial^2 f}{\partial x_1\,\partial x_n} \\[4ex] \cfrac{\partial g}{\partial x_2} & \cfrac{\partial^2 f}{\partial x_2\,\partial x_1} & \cfrac{\partial^2 f}{\partial x_2^2} & \cdots & \cfrac{\partial^2 f}{\partial x_2\,\partial x_n} \\[3ex] \vdots & \vdots & \vdots & \ddots & \vdots \\[3ex] \cfrac{\partial g}{\partial x_n} & \cfrac{\partial^2 f}{\partial x_n\,\partial x_1} & \cfrac{\partial^2 f}{\partial x_n\,\partial x_2} & \cdots & \cfrac{\partial^2 f}{\partial x_n^2}\end{pmatrix}](https://mathority.org/wp-content/ql-cache/quicklatex.com-3d1b2b04de9559a521e6704151c27bc4_l3.png)
Schritt 4: Wir ermitteln für jeden kritischen Punkt, ob es sich um ein Maximum oder ein Minimum handelt:
- Dies ist ein lokales Maximum der Funktion

unter Funktionseinschränkungen
wenn die letzten nm (wobei n die Anzahl der Variablen und m die Anzahl der Einschränkungen ist) Hauptminorwerte der am kritischen Punkt ausgewerteten umrandeten Hesse-Matrix abwechselnde Vorzeichen haben, beginnend mit dem negativen Vorzeichen.
- Dies ist ein lokales Minimum der Funktion

unter Funktionseinschränkungen
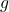
wenn die letzten nm (wobei n die Anzahl der Variablen und m die Anzahl der Einschränkungen ist) die Hauptminorwerte der am kritischen Punkt ausgewerteten scharfen Hesse-Matrix alle negative Vorzeichen haben.
Es ist zu beachten, dass die relativen Minima oder Maxima einer eingeschränkten Funktion zu einer anderen nicht unbedingt auch für die uneingeschränkte Funktion gelten müssen. Die umrandete Hesse-Matrix ist daher nur für diese Art von Problem nützlich.
Beziehung zu anderen Operationen
Schließlich ist die Hesse-Matrix auch mit anderen wichtigen Operationen oder Matrizen verknüpft, hauptsächlich mit der Jacobi-Matrix und mit dem Laplace-Operator.
Beziehung zur Jacobi-Matrix
Die Hessesche Matrix einer Funktion
![]()
ist die Jacobi-Matrix des Gradienten derselben Funktion:
![]()
Laplace-Operator
Die Hesse-Matrix-Spur entspricht dem Laplace-Operator :
![]()
Diese Gleichheit lässt sich leicht beweisen, da die Definition des Laplace-Operators die Divergenz des Gradienten einer Funktion ist:
![]()
Sein Ausdruck lautet daher:
![]()
Und diese Summe ist nur die Spur der Hesse-Matrix, also ist die Äquivalenz bewiesen.