Antihermitesche (oder antihermitesche) matrix

Auf dieser Seite sehen Sie, was eine antihermitesche Matrix, auch antihermitesche Matrix genannt, ist. Sie finden Beispiele für antihermitesche Matrizen, alle ihre Eigenschaften und die Form dieser Art komplexer quadratischer Matrizen. Abschließend finden Sie eine Erklärung, wie Sie eine komplexe Matrix in die Summe einer antihermiteschen Matrix und einer weiteren hermiteschen Matrix zerlegen.

Was ist eine antihermitesche oder antihermitesche Matrix?

Aus Neugier wird dieser Matrixtyp so genannt, weil er die entgegengesetzte Bedingung der hermiteschen Matrix erfüllt, deren Name von dem bedeutenden französischen Mathematiker Charles Hermite stammt, einem Mathematikprofessor und Forscher des 19. Jahrhunderts, der wichtige Studien unter anderem in durchgeführt hat das Gebiet der linearen Algebra.

Beispiele für antihermitesche Matrizen

Sobald wir die Definition der antihermiteschen Matrix (oder antihermiteschen Matrix) gesehen haben, werden wir einige Beispiele für antihermitesche Matrizen unterschiedlicher Dimensionen sehen:

Beispiel einer antihermiteschen Matrix der Ordnung 2×2

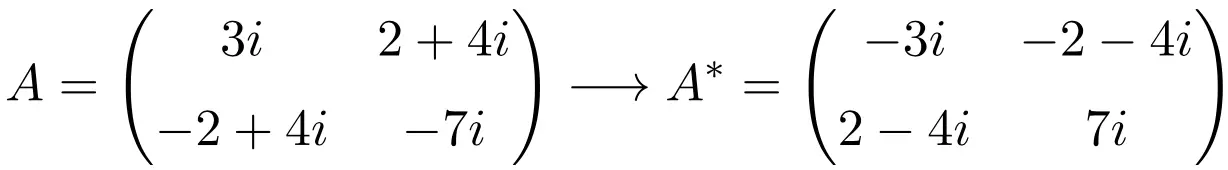
Beispiel einer antihermiteschen Matrix der Dimension 3×3

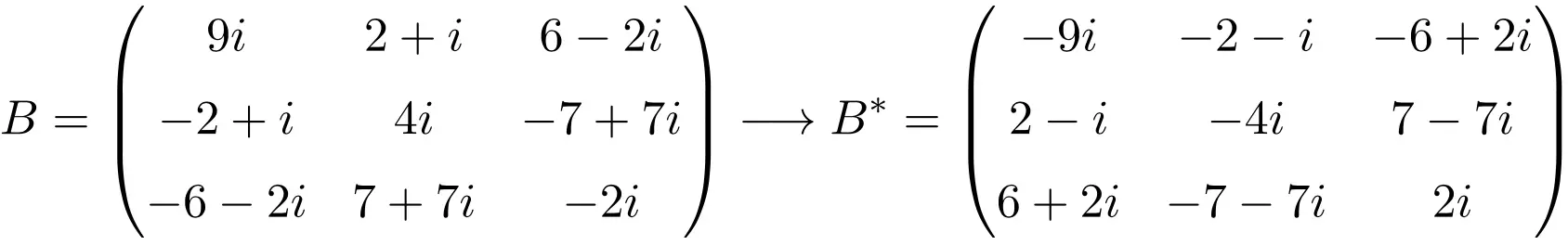
Beispiel einer antihermiteschen Matrix der Größe 4×4

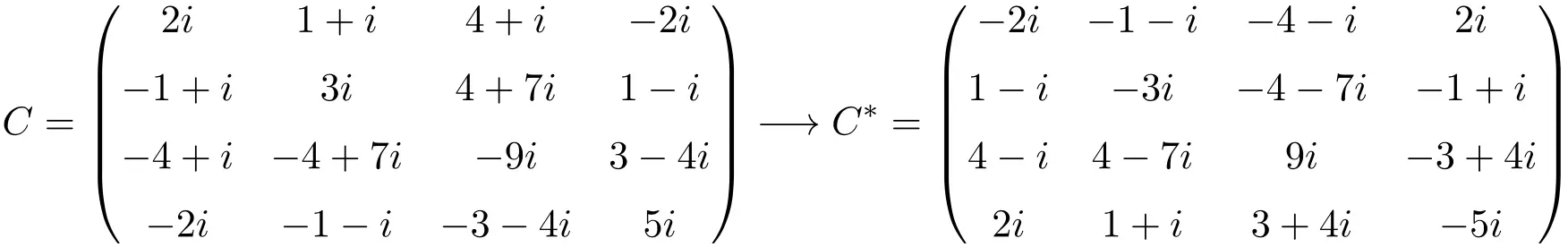
Wie Sie sehen können, sind die Matrizen A, B und C antihermitesch, da die konjugierte Transponierungsmatrix jeder Matrize gleich der Matrix selbst ist, jedoch alle Elemente ein geändertes Vorzeichen haben.

Struktur einer antihermiteschen Matrix

Wenn Sie sich die vorherigen Beispiele bereits angesehen haben, haben antihermitesche Matrizen immer die gleiche Struktur: Sie bestehen aus imaginären Zahlen (ohne Realteil) auf der Hauptdiagonale und dem komplexen Element, das auf der i-ten Linie und der j-ten Linie liegt Linie. Die Spalte muss denselben Imaginärteil und denselben Realteil, aber geändertes Vorzeichen haben wie das Element der j-ten Zeile und der i-ten Spalte.

Obwohl dies etwas kompliziert erscheinen mag, lässt es sich anhand des folgenden Beispiels sicherlich besser verstehen:

Struktur einer antihermiteschen Matrix der Dimension 2×2

Wie Sie sehen können, sind die Elemente der Hauptdiagonale einer antihermiteschen Matrix vollständig imaginär und die Elemente der Nebendiagonale haben den gleichen Imaginärteil und der Realteil hat das Vorzeichen geändert.

Daher muss der Realteil einer antihermiteschen Matrix antisymmetrisch und der Imaginärteil symmetrisch sein.

Eigenschaften der antihermitischen Matrix

Wir werden nun sehen, welche Eigenschaften diese Art von quadratischer komplexer Matrix hat:

• Jede antihermitesche Matrix ist ein Beispiel für eine Normalmatrix . Allerdings sind nicht alle normalen Matrizen antihermitische Matrizen.

• Jede antihermitesche Matrix ist diagonalisierbar. Darüber hinaus enthält die resultierende Diagonalmatrix nur rein imaginäre Elemente.

• Daher sind die Eigenwerte (oder Eigenwerte) einer antihermiteschen Matrix immer imaginäre Zahlen.

• Ebenso sind die Eigenvektoren (oder Eigenvektoren) verschiedener Eigenwerte einer antihermiteschen Matrix orthogonal.

• Eine Matrix reeller Zahlen, das heißt, dass kein Element einen Imaginärteil hat, ist genau dann antihermitesch, wenn es sich um eine antisymmetrische Matrix handelt.

• Eine antihermitesche Matrix kann als Summe einer realen antisymmetrischen Matrix und einer imaginären symmetrischen Matrix ausgedrückt werden.

• Die Summe (oder Subtraktion) zweier antihermitescher Matrizen ist gleich einer anderen antihermiteschen Matrix.

• Das Ergebnis des Produkts einer antihermiteschen Matrix und eines Skalars ist eine weitere antihermitesche Matrix, wenn der Skalar eine reelle Zahl ist.

• Die Potenz einer antihermiteschen Matrix ist gleich der einer antihermiteschen Matrix, wenn der Exponent ungerade ist; Wenn sie hingegen auf einen geraden Exponenten erhöht wird, ist das Ergebnis eine hermitesche Matrix.

• Ja

  

  ist eine antihermitesche Matrix, dann das Produkt

  

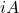
  ist eine hermitesche Matrix.

Zerlegung einer komplexen Matrix in eine antihermitesche Matrix und eine hermitesche Matrix

Jede Matrix, die komplexe Zahlen enthält, kann in die Summe einer antihermiteschen Matrix und einer weiteren hermiteschen Matrix zerlegt werden. Dazu müssen Sie jedoch die folgenden Eigenschaften dieser Matrizentypen kennen:

• Die Summe einer quadratischen komplexen Matrix plus ihrer transponierten Konjugierten entspricht einer hermiteschen (oder hermiteschen) Matrix:

• Der Unterschied zwischen einer quadratischen komplexen Matrix und ihrem transponierten Konjugat entspricht einer antihermiteschen Matrix:

• Daher können alle komplexen Matrizen in die Summe einer hermiteschen Matrix und einer antihermiteschen Matrix zerlegt werden. Dieser Satz ist als Teoplitz-Zerlegung bekannt:

Dabei ist C die komplexe Matrix, die wir zerlegen möchten, C* ihr transponiertes Konjugat und schließlich sind A und B die hermitesche bzw. antihermitesche Matrize, in die die Matrix C zerlegt wird.