Hier erfahren Sie, wie Sie die Kosinusfunktion (Formel) herleiten. Sie können Beispiele für Ableitungen von Kosinusfunktionen sehen und mit Schritt-für-Schritt-Übungen üben. Darüber hinaus zeigen wir Ihnen den Beweis der Formel, was die zweite Ableitung des Kosinus und sogar die Ableitung des inversen Kosinus ist.
Was ist die Ableitung des Kosinus?
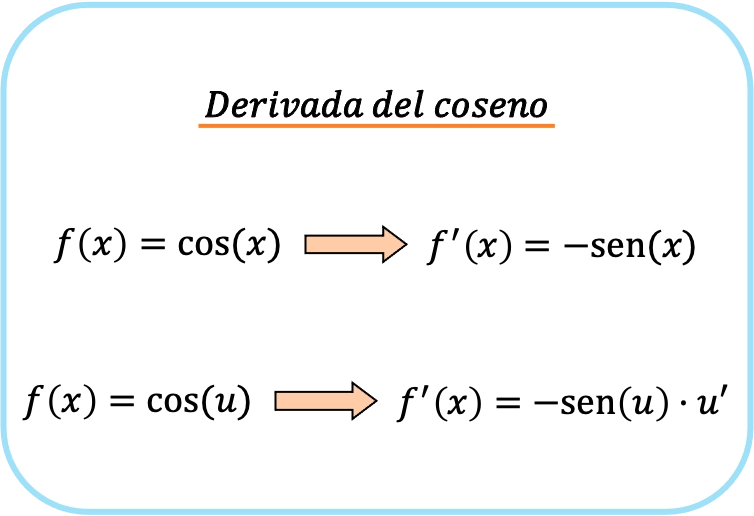
Die Ableitung der Kosinusfunktion ist die vorzeichenmodifizierte Sinusfunktion. Mit anderen Worten, die Ableitung des Kosinus von x ist gleich minus dem Sinus von x.
![]()
Wenn das Kosinusargument eine Funktion enthält, ist die Ableitung des Kosinus das Produkt aus minus dem Sinus dieser Funktion und der Ableitung der Funktion.
![]()
Die zweite Formel entspricht der ersten Formel, wendet jedoch die Kettenregel an. Zusammenfassend lautet die Formel für die Ableitung des Kosinus also wie folgt:
Beispiele für Kosinusableitungen
Nachdem wir nun wissen, was die Kosinusformel ist, erklären wir einige Beispiele dieser Art trigonometrischer Ableitungen, damit Sie keine Zweifel daran haben, wie man die Kosinusfunktion ableitet.
Beispiel 1: Ableitung des Kosinus von 2x
![]()
Im Kosinusargument haben wir kein einzelnes x, sondern eine komplexere Funktion. Daher müssen wir die folgende Formel verwenden, um den Kosinus abzuleiten:
![]()
Da die Ableitung von 2x 2 ist, ist die Ableitung des Kosinus von 2x minus dem Sinus von 2x multipliziert mit 2.
![]()
Beispiel 2: Ableitung des Kosinus von x im Quadrat
![]()
Wie im vorherigen Beispiel haben wir im Kosinusargument eine andere Funktion als x, daher verwenden wir die Kettenregel, um den Kosinus abzuleiten:
![]()
Dann ist die Ableitung von x 2 2x, daher ist die Ableitung des Kosinus von x hoch 2:
![]()
Beispiel 3: Ableitung des Kubikkosinus
![]()
Die Kosinusfunktion in diesem Beispiel besteht aus einer anderen Funktion, daher müssen wir die folgende Formel anwenden, um die Ableitung zu lösen:
![]()
Durch Anwendung der Formel gelangen wir also zur Ableitung der Funktion:
![Rendered by QuickLaTeX.com \begin{aligned}f'(x)&=3\text{cos}^2(2x^6-5x^3)\cdot \bigl(-\text{sen}(2x^6-5x^3)\bigr)\cdot (12x^5-15x^2)\\[2ex]&=-3\text{cos}^2(2x^6-5x^3)\cdot \text{sen}(2x^6-5x^3)\cdot (12x^5-15x^2)\end{aligned}](https://mathority.org/wp-content/ql-cache/quicklatex.com-73284bcfb1d5647b2304e323e7fbaedf_l3.png)
➤ Um diese Funktion zu differenzieren, müssen Sie auch die Formel für die Ableitung einer Potentialfunktion verwenden.
Zweite Ableitung des Kosinus
Als nächstes werden wir sehen, dass die zweite Ableitung des Sinus dank der Eigenschaften trigonometrischer Funktionen leicht berechnet werden kann.
➤ Hinweis: Um Folgendes zu verstehen, müssen Sie die Ableitung des Sinus kennen.
Die zweite Ableitung des Kosinus von x ist minus dem Kosinus von x. Das mag seltsam erscheinen, aber mathematisch ist es so. Tatsächlich ist die Ableitung des Sinus der Kosinus, und wenn man also den Kosinus von x zweimal differenziert, erhält man wieder den Kosinus, jedoch mit einem geänderten Vorzeichen.
![Rendered by QuickLaTeX.com \begin{array}{c}f(x)=\text{cos}(x)\\[1.5ex] \quad\color{orange}\bm{\downarrow}\quad\color{black} \\[1.5ex] f'(x)=-\text{sen}(x)\\[2ex] \quad\color{orange}\bm{\downarrow}\quad\color{black} \\[1.5ex] f''(x)=-\text{cos}(x)\end{array}](https://mathority.org/wp-content/ql-cache/quicklatex.com-d0d9dda8a4031c367120b1f950da4391_l3.png)
Diese Eigenschaft ändert sich, wenn das Kosinusargument nicht x ist, da wir in diesem Fall den Term der Kettenregel ziehen:
![Rendered by QuickLaTeX.com \begin{array}{c}f(x)=\text{cos}(u)\\[1.5ex] \quad\color{orange}\bm{\downarrow}\quad\color{black} \\[1.5ex] f'(x)=-\text{sen}(u)\cdot u' \\[1.5ex] \quad\color{orange}\bm{\downarrow}\quad\color{black} \\[1.5ex] f''(x)=-\text{cos}(u)\cdot u'^2 -\text{sen}(u)\cdot u'' \end{array}](https://mathority.org/wp-content/ql-cache/quicklatex.com-83d86bd6508f06b0723153b3b9254c1f_l3.png)
Ableitung des Umkehrkosinus
Alle trigonometrischen Funktionen haben eine Umkehrfunktion und daher kann auch die Kosinusfunktion umgekehrt werden. Ebenso ist der Umkehrkosinus differenzierbar.
Die Ableitung des Umkehrkosinus einer Funktion ist minus der Ableitung der Funktion dividiert durch die Quadratwurzel aus eins minus dem Quadrat dieser Funktion.
![]()
Denken Sie daran, dass der Umkehrkosinus auch Arkuskosinus genannt wird.
Die Ableitung des Umkehrkosinus von 3x lautet beispielsweise:
![]()
Aufgaben zur Ableitung des Kosinus gelöst
Berechnen Sie die Ableitung der folgenden Kosinusfunktionen:
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![Rendered by QuickLaTeX.com \begin{aligned}\text{F) }\displaystyle f'(x)&=-9\text{sen}\left(\frac{e^x}{5x}\right)\cdot \frac{e^x\cdot 5x-e^x\cdot 5}{(5x)^2}\\[2ex]&=-9\text{sen}\left(\frac{e^x}{5x}\right)\cdot \frac{5e^x(x-1)}{25x^2}\\[2ex]&=-9\text{sen}\left(\frac{e^x}{5x}\right)\cdot \frac{e^x(x-1)}{5x^2}\end{aligned}](https://mathority.org/wp-content/ql-cache/quicklatex.com-9f4645fb77435daec6f696cffbd54884_l3.png)
Beweis der Kosinusableitung
Abschließend werden wir die Formel für die Ableitung des Kosinus von x mathematisch demonstrieren. Dazu verwenden wir die Definition der Ableitung, die der folgenden Grenze entspricht:
![]()
Wir werden den Kosinus beweisen, also ist die Funktion cos(x):
![]()
Wir können diese Grenze nicht durch Substitution auflösen, da wir sonst in der Unbestimmtheit enden würden. Wir können den Kosinus einer Summe jedoch auch auf andere Weise ausdrücken, indem wir die folgende trigonometrische Identität anwenden:
![]()
![]()
Der nächste Schritt besteht darin, den Bruch in zwei Brüche aufzuteilen und den gemeinsamen Faktor des Kosinus zu bilden:
![Rendered by QuickLaTeX.com \displaystyle f'(x)=\lim_{h \to 0}\left[\frac{\text{cos}(x)\bigl(\text{cos}(h)-1\bigr)}{h}-\frac{\text{sen}(x)\text{sen}(h)}{h}\right]](https://mathority.org/wp-content/ql-cache/quicklatex.com-c7c1cd89cf290b01d7d72fc8084f6529_l3.png)
Der Grenzwert einer Subtraktion ist gleich der Subtraktion der Grenzwerte, daher:
![]()
Der Kosinus von x und der Sinus von x hängen nicht von h ab, daher können wir sie außerhalb der Grenzen extrahieren:
![]()
Mithilfe der Berechnung von Grenzwerten anhand von Infinitesimaläquivalenten kommen wir zu dem Schluss, dass der erste Grenzwert 0 und der zweite Grenzwert 1 ist. Daher:
![]()
![]()
Und wir sind bereits bei der Formel für die Ableitung der Kosinusfunktion angelangt, die Gleichheit ist also bewiesen.