Komplexe, konjugierte und transponierte Matrix

Auf dieser Seite erfahren Sie, was komplexe Matrizen, konjugierte Matrizen und konjugierte transponierte Matrizen sind. Jetzt sehen sie Ihnen sehr ähnlich, aber Sie werden sehen, dass Sie am Ende der Seite den Unterschied zwischen den einzelnen vollständig verstehen werden. Darüber hinaus sehen wir Beispiele für jeden Typ und seine Eigenschaften.

komplexe Matrix

Bevor wir uns die Erklärung der konjugierten Matrix und der transponierten konjugierten Matrix ansehen, werfen wir einen Blick auf das Konzept der komplexen Matrix:

Was ist eine komplexe Matrix?

Eine komplexe Matrix ist eine Matrix, deren Elemente eine bestimmte komplexe Zahl aufweisen.

Denken Sie daran, dass eine komplexe oder imaginäre Zahl eine Zahl ist, die aus einem Realteil und einem Imaginärteil besteht, was durch den Buchstaben i angegeben wird. Zum Beispiel:

$3+5i$

Beispiele für komplexe Matrizen

Schauen wir uns einige Beispiele für komplexe mehrdimensionale Arrays an:

Beispiel einer komplexen Matrix der Ordnung 2 × 2

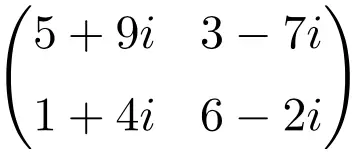
Beispiel einer komplexen Matrix der Dimension 3×3

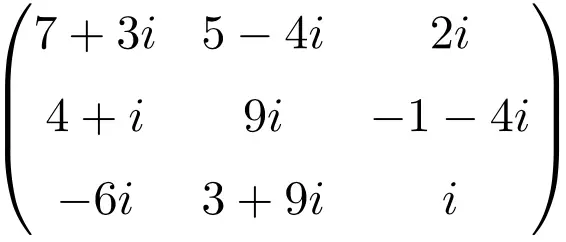
Beispiel einer komplexen Matrix der Größe 4×4

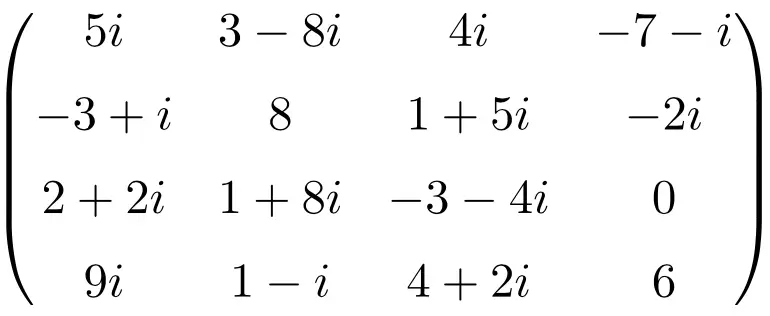
konjugierte Matrix

Nachdem wir gesehen haben, was die Definition einer komplexen Matrix ist, sehen wir uns an, was eine konjugierte Matrix und eine transponierte konjugierte Matrix sind:

Was ist eine konjugierte Matrix?

Eine konjugierte Matrix ist eine komplexe Matrix, in der alle ihre Elemente durch ihre Konjugate ersetzt wurden, d. h. das Vorzeichen des Imaginärteils aller ihrer komplexen Zahlen wurde geändert.

Die konjugierte Matrix von

$A$

wird durch einen horizontalen Balken oben ausgedrückt:

$\overline{A}$

Beispiel einer konjugierten Matrix

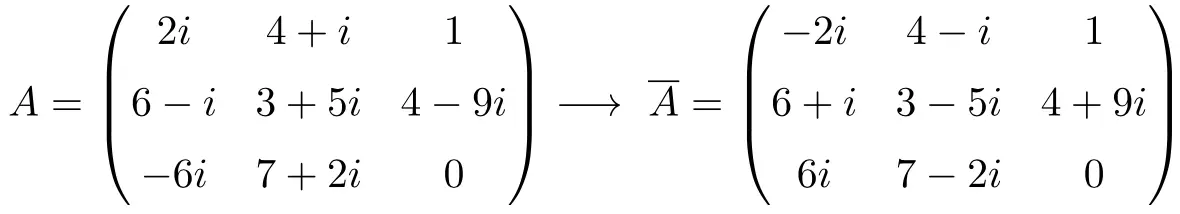
Beispiel für eine Matrixkonjugation, wie man eine Matrix konjugiert

Eigenschaften der konjugierten Matrix

Die Merkmale dieses Matrixtyps sind wie folgt:

Das Konjugat einer konjugierten Matrix ist die Originalmatrix.

$\displaystyle \overline{\bigl( \ \overline{A} \vphantom{A^{9^1}} \ \bigr)} = A$

Das Addieren (oder Subtrahieren) zweier Matrizen und das Konjugieren des Ergebnisses ist dasselbe, als würde man die beiden Matrizen zunächst getrennt konjugieren und sie dann addieren (oder subtrahieren).

$\displaystyle \overline{\bigl( A \pm B \bigr)} = \overline{A} \pm \overline{B}$

Das konjugierte Produkt zweier Matrizen entspricht der getrennten Konjugation der beiden Matrizen und der anschließenden Berechnung der Matrixmultiplikation.

$\displaystyle \overline{\bigl( A \cdot B \bigr)} = \overline{A} \cdot \overline{B}$

Das Multiplizieren einer Matrix mit einem Skalar und das Konjugieren des Ergebnisses ist dasselbe, als würde man zunächst den Skalar und die Matrix konjugieren und dann nach dem Produkt auflösen.

$\displaystyle \overline{\bigl( k \cdot A \bigr)} = \overline{k} \cdot \overline{A}$

Eine Matrix zu transponieren und dann zu konjugieren bedeutet, zuerst die Matrix zu konjugieren und sie dann zu transponieren.

$\displaystyle \overline{\bigl(A^t \bigr)} = \left( \overline{A}\right)^t$

Die Umkehrung einer Matrix und deren anschließende Konjugation ist dasselbe wie die Konjugation der Matrix und deren anschließende Invertierung.

$\displaystyle \overline{\bigl( A^{-1} \bigr)} = \left(\overline{A} \right)^{-1}$

Der Rang einer konjugierten Matrix ist gleich dem Rang derselben unkonjugierten Matrix.

$\displaystyle rg\left(\overline{A}\right) =rg(A)$

Es ist gleichgültig, die Spur einer konjugierten Matrix zu berechnen oder die Spur derselben Matrix ohne Konjugation zu berechnen und dann das Ergebnis zu konjugieren.

$\displaystyle tr\left(\overline{A}\right) =\overline{tr(A)}$

Schließlich läuft die Verwendung der Determinante einer konjugierten Matrix darauf hinaus, die Konjugation des Ergebnisses der Determinante derselben Matrix ohne Konjugation zu berechnen.

$\displaystyle det\left(\overline{A}\right) = \overline{det(A)}$

Konjugierte Transponierungsmatrix

Nachdem wir schließlich gesehen haben, wie man eine Matrix konjugiert, wenden wir uns nun dem Konzept einer konjugierten Transponierungsmatrix zu:

Was ist eine konjugiert transponierte (oder transponierte) Matrix?

Die transponierte (oder transponierte) konjugierte Matrix ist diejenige, die erhalten wird, nachdem eine Matrix transponiert und dann konjugiert wurde.

Diese Art von Matrix wird auch adjungierte Matrix oder einfach adjungierte Matrix genannt. Darüber hinaus wird es normalerweise durch ein Sternchen dargestellt

$(A^*)$

, obwohl es Mathematiker gibt, die es so zeichnen

$A^*$

entweder

$A^H$

Beispiel einer konjugierten Transponierungsmatrix

Hier ist ein Beispiel für die Berechnung der Transponierten (oder konjugierten Transponierten) einer Matrix:

$\displaystyle A=\begin{pmatrix}1+3i&2-i & -4i \\[1.1ex] 6 & 8+2i & 3-5i \\[1.1ex] 7i & 1+9i & -2+i\end{pmatrix}$

Wir transponieren zunächst die Matrix A:

$\displaystyle A^t=\begin{pmatrix}1+3i& 6 & 7i \\[1.1ex] 2-i & 8+2i & 1+9i \\[1.1ex] -4i & 3-5i & -2+i\end{pmatrix}$

Und dann berechnen wir die konjugierte Matrix der Transponierten, oder anders ausgedrückt, wir ändern das Vorzeichen des Imaginärteils aller komplexen Zahlen:

$\displaystyle A^*=\overline{A^t}=\begin{pmatrix}1-3i& 6 & -7i \\[1.1ex] 2+i & 8-2i & 1-9i \\[1.1ex] 4i & 3+5i & -2-i\end{pmatrix}$

Daher lautet die Zusammenfassung der Berechnung der konjugierten Transponierungsmatrix:

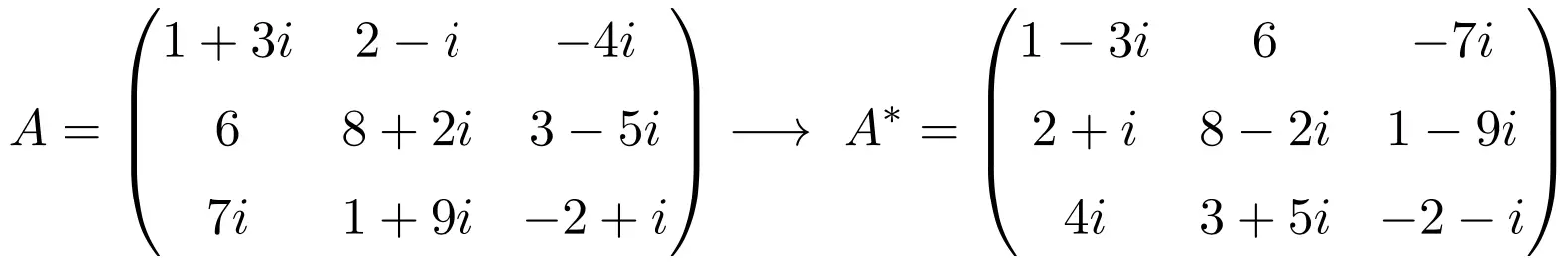
konjugierte transponierte Matrix der Dimension 3x3

Eigenschaften der konjugierten Transponierungsmatrix

Die Eigenschaften dieser Art von quadratischer Matrix sind wie folgt:

Die konjugierte Transponierungsmatrix einer zuvor transponierten und konjugierten Matrix ist die Originalmatrix.

$\displaystyle \bigl(A^*\bigr) ^* = A$

Die Additionseigenschaft konjugiert transponierter Matrizen besagt, dass das Addieren (oder Subtrahieren) zweier Matrizen und das anschließende Anwenden dieser Operation auf das Ergebnis gleichbedeutend damit ist, zuerst die konjugierte Transponierung jeder Matrix durchzuführen und dann die Ergebnisse zu addieren (oder zu subtrahieren).

$\displaystyle \bigl( A\pm B \bigr)^* = A^*\pm B^*$

Die Multiplikation zweier Matrizen und deren anschließende konjugierte Transponierung ergibt das gleiche Ergebnis wie das Umkehrprodukt der konjugiert transponierten Matrizen.

$\displaystyle \bigl( A\cdot B \bigr)^* = B^*\cdot A^*$

Die Berechnung der konjugierten Transponiertenmatrix des Produkts aus einem Skalar und einer Matrix ist dasselbe, als würde man die komplexe Zahl konjugieren und die konjugierte Transponierte der Matrix separat ermitteln und dann multiplizieren.

$\displaystyle \bigl( k\cdot A \bigr)^* = \overline{k}\cdot A^*$

Wenn die Matrix invertierbar ist, ist die Reihenfolge, in der die Operationen Matrixinversion und konjugierte Transponierung ausgeführt werden, irrelevant.

$\displaystyle \bigl( A^{-1} \bigr)^*= \bigl( A^* \bigr)^{-1}$

Komplexe, konjugierte und transponierte matrix