Auf dieser Seite erklären wir, was der unabhängige Term eines Polynoms ist und wie er berechnet wird. Darüber hinaus können Sie mehrere Beispiele zur Identifizierung des unabhängigen Termes verschiedener Polynome sehen und sogar anhand gelöster Aufgaben üben.
Was ist der unabhängige Term eines Polynoms?
Die Definition des unabhängigen Termes eines Polynoms lautet wie folgt:
In der Mathematik ist der unabhängige Term eines Polynoms der Term, der keine Variable hat. Daher entspricht der unabhängige Term eines Polynoms dem Monom nullten Grades des Polynoms.
Der unabhängige Term des folgenden Polynoms ist beispielsweise 7:
![]()
Im Polynom des vorherigen Beispiels ist der Term, der keinen Literalteil hat, also kein x hat, die Zahl 7. Aus diesem Grund ist der unabhängige Term dieses Polynoms 7.
Obwohl der unabhängige Term eines Polynoms ein sehr einfaches Konzept zu sein scheint, sollten Sie wissen, dass er für einige Polynomberechnungen sehr nützlich ist. Beispielsweise beginnt das Verfahren zum Finden der Wurzeln eines Polynoms bei seinem unabhängigen Term. Wenn Sie mehr darüber erfahren möchten, wie Sie die Wurzeln (oder Nullstellen) eines Polynoms finden, können Sie sich diesen Link ansehen, wo Sie auch Beispiele sehen und mit Schritt für Schritt gelösten Übungen üben können.
Beispiele für unabhängige Terme von Polynomen
Sobald wir die Bedeutung des unabhängigen Termes eines Polynoms kennen, werden wir mehrere Beispiele sehen, wie man den unabhängigen Term eines Polynoms findet:
- Beispiel für einen unabhängigen Term eines Polynoms vom Grad 4:
![]()
Das Polynom in diesem Beispiel ist ein monisches Polynom und der Term ohne Variable ist 5, sodass der Wert des unabhängigen Termes des Polynoms 5 ist.
- Beispiel für einen unabhängigen Term eines Polynoms vom Grad 5:
![]()
Das Element dieses Polynoms, das nicht von der Variablen x begleitet wird, ist -2, es ist daher der unabhängige Term des Polynoms. Beachten Sie, dass das negative Vorzeichen der Zahl auch im unabhängigen Term enthalten ist.
- Beispiel für einen unabhängigen Term eines Polynoms vom Grad 8:
![]()
Alle Monome in diesem Polynom haben eine Variable außer +1, daher ist der unabhängige Term des Polynoms +1.
Schließlich besteht eine der Eigenschaften des unabhängigen Termes darin, dass der numerische Wert eines Polynoms für x=0 immer gleich seinem unabhängigen Term ist. Wenn Sie sich mehr für diese kuriose Sache interessieren, können Sie auf der verlinkten Seite nachlesen, wie der numerische Wert eines Polynoms berechnet wird. Außerdem finden Sie dort auch mehrere Beispiele dafür und können anhand gelöster Übungen üben Schritt für Schritt.
Übung zum unabhängigen Term eines Polynoms gelöst
Um den unabhängigen Term eines Polynoms vollständig zu verstehen, empfehlen wir Ihnen, die unten gelöste Übung durchzuführen:
- Gegeben sei das Polynom
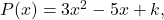
berechnet den Wert des unabhängigen Termes

damit es gefüllt ist
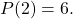
Um dieses Problem zu lösen, müssen Sie zunächst versuchen, es festzustellen
![]()
Noch:
![]()
Wir berechnen die Leistung:
![]()
Wir machen die Multiplikationen:
![]()
Und wir subtrahieren als Terme:
![]()
Damit die Bedingung der Aussage erfüllt ist, ist es daher notwendig, den erhaltenen algebraischen Ausdruck auf 6 anzugleichen:
![]()
![]()
Es reicht daher aus, die resultierende Gleichung zu lösen:
![]()
![]()
Zusammenfassend muss der unabhängige Term des Polynoms 4 sein.
Schließlich sollten Sie wissen, dass auch der unabhängige Term eines Polynoms wichtig ist, um die Ruffini-Regel korrekt anzuwenden. Falls Sie nicht wissen, was es ist: Ruffinis Regel ist eine Methode zur schnellen Division von Polynomen. Hier können Sie sehen , wie die Ruffini-Regel angewendet wird und wie sie sich auf den unabhängigen Term eines Polynoms bezieht.