Gaußsche Methode

Auf dieser Seite erfahren Sie, was die Gauß-Jordan-Methode ist und wie Sie ein Gleichungssystem mit der Gauß-Methode lösen. Darüber hinaus finden Sie auch Beispiele und gelöste Aufgaben zu Systemen mit der Gauß-Methode, damit Sie diese perfekt üben und verstehen können.

Was ist die Gauß-Methode?

Die Gauß-Jordan-Methode ist ein Verfahren zur Lösung von Gleichungssystemen mit 3 Unbekannten, also wie folgt:

$\left. \begin{array}{r} 3x-4y+5z=10 \\[2ex] x+5y-2z=4 \\[2ex] -x+4y+2z=-1 \end{array} \right\}$

Das Ziel der Gauß-Methode besteht darin, das ursprüngliche Gleichungssystem in ein Stufensystem umzuwandeln, d. h. ein System, in dem jede Gleichung eine weniger unbekannte Unbekannte aufweist als die vorherige:

$\left. \begin{array}{r} a_1x+b_1y+c_1z=d_1 \\[2ex] a_2x+b_2y+c_2z=d_2 \\[2ex] a_3x+b_3y+c_3z=d_3 \end{array} \right\} \ \bm{\longrightarrow} \left. \begin{array}{r} A_1x+B_1y+C_1z=D_1 \\[2ex] B_2y+C_2z=D_2 \\[2ex] C_3z=D_3 \end{array} \right\}$

Dazu müssen Sie jedoch zunächst wissen, wie man ein Gleichungssystem in Matrixform ausdrückt und welche Transformationen auf dieser Matrix zulässig sind . Deshalb werden wir diese beiden Dinge vorher erklären und dann sehen, wie man das Verfahren der Gauß-Methode verwendet.

Systemerweiterte Matrix

Bevor Sie sehen, wie das System gelöst wird, müssen Sie wissen, dass ein Gleichungssystem in Form einer Matrix ausgedrückt werden kann: die Koeffizienten der

$x}$

In die erste Spalte werden die Koeffizienten eingetragen

$y}$

in der zweiten Spalte die Koeffizienten der

$z$

in der dritten Spalte und Zahlen ohne Unbekannte in der vierten Spalte.

Zum Beispiel:

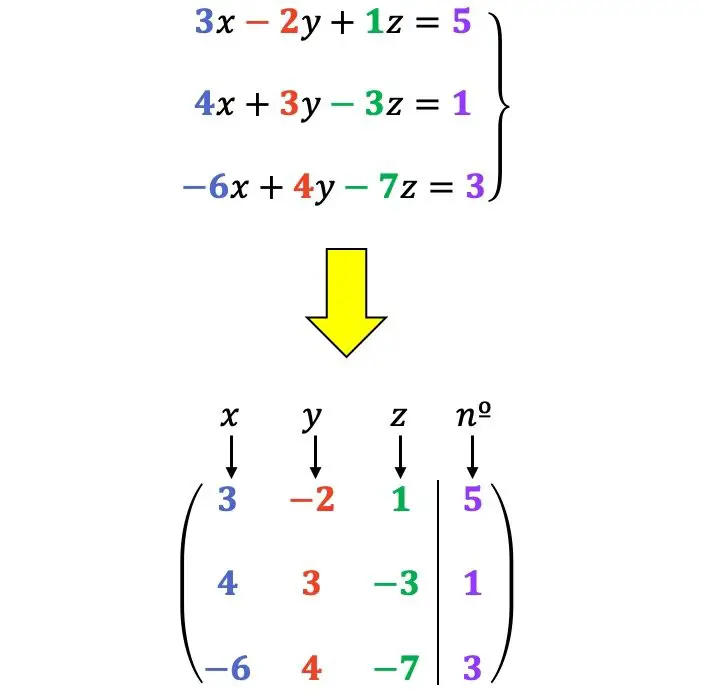
Zulässige Zeilentransformationen

Um das Gleichungssystem in ein skaliertes System umzuwandeln, kann eine der folgenden Operationen an der dem System zugeordneten Matrix durchgeführt werden:

Ändern Sie die Reihenfolge der Zeilen in der Matrix.

Beispielsweise können wir die Reihenfolge der Zeilen 2 und 3 einer Matrix ändern:

$\left( \begin{array}{ccc|c} 3 & 5 & -2 & 1 \\[2ex] -2 & 4 & -1 & 2 \\[2ex] 6 & 1 & -3 & 10 \end{array} \right) \begin{array}{c} \\[2ex] \xrightarrow{ f_2 \rightarrow f_3}} \\[2ex] \xrightarrow{ f_3 \rightarrow f_2}} \end{array} \left( \begin{array}{ccc|c} 3 & 5 & -2 & 1 \\[2ex] 6 & 1 & -3 & 10 \\[2ex] -2 & 4 & -1 & 2 \end{array} \right)$

Multiplizieren oder dividieren Sie alle Terme in einer Zeile mit einer Zahl ungleich 0.

Wir können zum Beispiel Zeile 1 mit 4 multiplizieren und Zeile 3 durch 2 dividieren:

$\left( \begin{array}{ccc|c} 1 & -2 & 3 & 1 \\[2ex] 3 & -1 & 5 & -3 \\[2ex] 2 & -4 & -2 & 6 \end{array} \right) \begin{array}{c} \xrightarrow{4 f_1} \\[2ex] \\[2ex] \xrightarrow{ f_3 / 2} \end{array} \left( \begin{array}{ccc|c} 4 & -8 & 12 & 4 \\[2ex] 3 & -1 & 5 & -3 \\[2ex] 1 & -2 & -1 & 3 \end{array} \right)$

Ersetzen Sie eine Zeile durch die Summe derselben Zeile plus einer anderen Zeile multipliziert mit einer Zahl.

In der folgenden Matrix addieren wir beispielsweise Zeile 2 zu Zeile 3 multipliziert mit 1:

$\left( \begin{array}{ccc|c} -1 & -3 & 4 & 1 \\[2ex] 2 & 4 & 1 & -5 \\[2ex] 1 & -2 & 3 & -1 \end{array} \right) \begin{array}{c} \\[2ex] \xrightarrow{f_2 + 1 \cdot f_3} \\[2ex] & \end{array} \left( \begin{array}{ccc|c} -1 & -3 & 4 & 1 \\[2ex] 3 & 2 & 4 & -6 \\[2ex] 1 & -2 & 3 & -1 \end{array} \right)$

Wie löst man ein Gleichungssystem mit der Gauß-Methode?

Wir sehen uns nun anhand eines Beispiels die Vorgehensweise zur Lösung eines Gleichungssystems mit der Gauß-Methode an:

$\left. \begin{array}{r} -x+2y+2z=-24 \\[2ex] x+y+z=48 \\[2ex] 2x-6y+4z=12 \end{array} \right\}$

Als erstes geht es um die erweiterte Matrix des Systems :

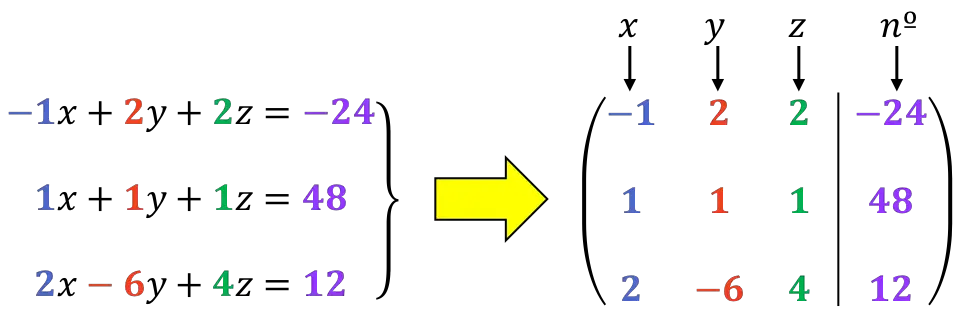
Beispiel eines mit der Gauß-Methode gelösten Gleichungssystems

Wie wir später sehen werden, ist es besser, wenn die erste Ziffer der ersten Zeile eine 1 ist. Wir werden daher die Reihenfolge der Zeilen 1 und 2 ändern:

$\left( \begin{array}{ccc|c} -1 & 2 & 2 &-24 \\[2ex] 1 & 1 & 1 & 48 \\[2ex] 2 & -6 & 4 & 12 \end{array} \right) \begin{array}{c} \xrightarrow{ f_1 \rightarrow f_2} \\[2ex] \xrightarrow{ f_2 \rightarrow f_1} \\[2ex] & \end{array} \left( \begin{array}{ccc|c} \color{blue}\boxed{\color{black}1} & 1 & 1 & 48 \\[2ex] -1 & 2 & 2 &-24 \\[2ex] 2 & -6 & 4 & 12 \end{array} \right)$

Das Ziel der Gauß-Methode besteht darin , die Zahlen unterhalb der Hauptdiagonale auf 0 zu bringen. Das heißt, wir müssen die roten Zahlen in 0 umwandeln:

$\left( \begin{array}{ccc|c} 1 & 1 & 1 & 48 \\[2ex] \color{red}\bm{-1} & 2 & 2 &-24 \\[2ex] \color{red}\bm{2} & \color{red}\bm{-6} & 4 & 12 \end{array} \right)$

Um diese Zahlen zu eliminieren, müssen wir die entsprechenden Transformationen der Zeilen durchführen.

Beispielsweise ist -1, das erste Element der zweiten Zeile, das Negative von 1, dem ersten Element der ersten Zeile. Wenn wir also die erste Zeile zur zweiten Zeile hinzufügen, wird -1 eliminiert:

$\begin{array}{lccc|c} & -1 & 2 & 2 & -24 \\ + & \phantom{-}1 & 1 & 1 & \phantom{-}48 \\ \hline & \phantom{-}0 & 3 & 3 & \phantom{-}24 \end{array} \begin{array}{l} \color{blue}\bm{\leftarrow f_2} \\ \color{blue}\bm{\leftarrow f_1} \\ \phantom{hline} \\ \end{array}$

Wenn wir also diese Summe bilden, erhalten wir die folgende Matrix:

$\left( \begin{array}{ccc|c} 1 & 1 & 1 & 48 \\[2ex] -1 & 2 & 2 & -24 \\[2ex] 2 & -6 & 4 & 12 \end{array} \right) \begin{array}{c} \\[2ex] \xrightarrow{f_2 + f_1} \\[2ex] & \end{array} \left( \begin{array}{ccc|c} 1 & 1 & 1 & 48 \\[2ex] \color{blue}\boxed{\color{black}0} & 3 & 3 & 24 \\[2ex] 2 & -6 & 4 & 12 \end{array} \right)$

Auf diese Weise ist es uns gelungen, -1 in eine 0 umzuwandeln.

Jetzt transformieren wir die 2. Wie Sie bemerken, ist die 2, das erste Element in der dritten Zeile, das Doppelte von 1, dem ersten Element in der ersten Zeile. Wenn wir also die erste Zeile multipliziert mit -2 zur dritten Zeile hinzufügen, wird die 2 eliminiert:

$\begin{array}{lccc|c} & \phantom{-}2 & -6 & \phantom{-}4 & \phantom{-}12 \\ + & -2 & -2 & -2 & -96 \\ \hline & \phantom{-}0 & -8 & \phantom{-}2 & -84 \end{array} \begin{array}{l} \color{blue} \bm{\leftarrow f_3} \\ \color{blue} \bm{\leftarrow -2 f_1} \\ \phantom{hline} \\ \end{array}$

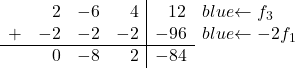
Somit erhalten wir folgende Matrix:

$\left( \begin{array}{ccc|c} 1 & 1 & 1 & 48 \\[2ex] 0 & 3 & 3 & 24 \\[2ex] 2 & -6 & 4 & 12 \end{array} \right) \begin{array}{c} \\[2ex] \\[2ex] \xrightarrow{f_3-2f_1} \end{array} \left( \begin{array}{ccc|c} 1 & 1 & 1 & 48 \\[2ex] 0 & 3 & 3 & 24 \\[2ex] \color{blue}\boxed{\color{black}0} & -8 & 2 & -84 \end{array} \right)$

Auf diese Weise ist es uns gelungen, die 2 in eine 0 umzuwandeln.

Jetzt müssen wir nur noch die -8 in 0 umwandeln. Dazu multiplizieren wir die dritte Zeile mit 3 und addieren die zweite Zeile multipliziert mit 8:

$\begin{array}{lccc|r} & 0 & -24 & \phantom{2}6 & -252 \\ + & 0 & \phantom{-}24 & 24 & \phantom{-}192 \\ \hline & 0 & \phantom{-2}0 & 30 & -60 \end{array} \begin{array}{l}\color{blue}\bm{ \leftarrow 3f_3} \\\color{blue}\bm{ \leftarrow 8f_2} \\ \phantom{hline} \\ \end{array}$

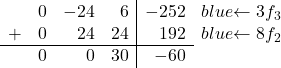
Wir erhalten daher die folgende Matrix:

$\left( \begin{array}{ccc|c} 1 & 1 & 1 & 48 \\[2ex] 0 & 3 & 3 & 24 \\[2ex] 0 & -8 & 2 & -84 \end{array} \right) \begin{array}{c} \\[2ex] \\[2ex] \xrightarrow{3f_3 + 8f_2} \end{array} \left( \begin{array}{ccc|c} 1 & 1 & 1 & 48 \\[2ex] 0 & 3 & 3 & 24 \\[2ex] 0 & \color{blue}\boxed{\color{black}0} & 30 & -60 \end{array} \right)$

Und mit diesen Transformationen haben wir alle Zahlen unterhalb der Hauptdiagonale auf 0 gebracht. Jetzt können wir das Gleichungssystem lösen.

Wir müssen nun die Matrix in ein Gleichungssystem mit Unbekannten umwandeln . Denken Sie dabei daran, dass die erste Spalte dem entspricht

$x$

, die zweite Spalte von

$y$

, die dritte Spalte von

$z$

und die letzte Spalte sind die Zahlen ohne Unbekannte:

$\left( \begin{array}{ccc|c} 1 & 1 & 1 & 48 \\[2ex] 0 & 3 & 3 & 24 \\[2ex] 0 & 0 & 30 & -60 \end{array} \right) \ \longrightarrow \ \left. \begin{array}{r} 1x+1y+1z=48 \\[2ex] 3y+3z=24 \\[2ex] 30z=-60 \end{array} \right\}$

Und schließlich müssen wir zur Lösung des Systems die Unbekannten der Gleichungen von unten nach oben lösen. Da die letzte Gleichung nur eine Unbekannte hat, können wir sie lösen und ihren Wert ermitteln:

$30z=-60$

$z = \cfrac{-60}{30}$

$\bm{z=-2}$

Da wir nun wissen, was z ist, können wir den Wert von ermitteln, wenn wir seinen Wert in die zweite Gleichung einsetzen

$y$

$3y+3z=24 \ \xrightarrow{z \ = \ -2} \ 3y+3(-2)=24$

$3y-6=24$

$3y=24+6$

$3y=30$

$y=\cfrac{30}{3}$

$\bm{y=10}$

Und das Gleiche machen wir mit der ersten Gleichung: Wir ersetzen die Werte der anderen Unbekannten und löschen sie

$x$

$1x+1y+1z=48 \ \xrightarrow{y \ = \ 10 \ ; \ z \ = \ -2} \ 1x+1(10)+1(-2)=48$

$x+10-2=48$

$x=48-10+2$

$\bm{x=40}$

Die Lösung des Gleichungssystems lautet daher:

$\bm{x=40} \quad \bm{y=10} \quad \bm{z=-2}$

Probleme von Gleichungssystemen nach der Gauß-Jordan-Methode gelöst

Übung 1

Lösen Sie das folgende Gleichungssystem mit der Gauß-Methode:

$\left. \begin{array}{r} x+y-z=2 \\[2ex] x-2y+3z=0 \\[2ex] 2x-y+3z=3 \end{array} \right\}$

siehe Lösung

Als erstes müssen wir die erweiterte Matrix des Systems erstellen:

$\left. \begin{array}{r} x+y-z=2 \\[2ex] x-2y+3z=0 \\[2ex] 2x-y+3z=3 \end{array} \right\} \longrightarrow \left( \begin{array}{ccc|c} 1 & 1 & -1 & 2 \\[2ex] 1 & -2 & 3 & 0 \\[2ex] 2 & -1 & 3 & 3 \end{array} \right)$

Jetzt müssen wir alle Zahlen unterhalb des Hauptarrays auf 0 setzen.

Wir führen daher Zeilenoperationen durch, um die letzten beiden Terme der ersten Spalte zu löschen:

$\left( \begin{array}{ccc|c}1 & 1 & -1 & 2 \\[2ex] 1 & -2 & 3 & 0 \\[2ex] 2 & -1 & 3 & 3 \end{array} \right) \begin{array}{c} \\[2ex] \xrightarrow{f_2 -f_1} \\[2ex] \xrightarrow{f_3-2f_1} & \end{array} \left( \begin{array}{ccc|c} 1 & 1 & -1 & 2 \\[2ex] 0 & -3 & 4 & -2 \\[2ex] 0 & -3 & 5 & -1 \end{array} \right)$

Jetzt entfernen wir das letzte Element aus der zweiten Spalte:

$\left( \begin{array}{ccc|c}1 & 1 & -1 & 2 \\[2ex] 0 & -3 & 4 & -2 \\[2ex] 0 & -3 & 5 & -1 \end{array} \right) \begin{array}{c} \\[2ex] \\[2ex] \xrightarrow{f_3-f_2} & \end{array} \left( \begin{array}{ccc|c} 1 & 1 & -1 & 2 \\[2ex] 0 & -3 & 4 & -2 \\[2ex] 0 & 0 & 1 & 1 \end{array} \right)$

Sobald alle Zahlen unterhalb der Hauptdiagonale 0 sind, können wir nun das Gleichungssystem lösen. Dazu drücken wir die Matrix noch einmal in Form eines Gleichungssystems mit Unbekannten aus:

$\left( \begin{array}{ccc|c} 1 & 1 & -1 & 2 \\[2ex] 0 & -3 & 4 & -2 \\[2ex] 0 & 0 & 1 & 1 \end{array} \right) \ \longrightarrow \ \left. \begin{array}{r} x+y-z=2 \\[2ex] -3y+4z=-2 \\[2ex] 1z=1 \end{array} \right\}$

Und wir lösen die Unbekannten der Gleichungen von unten nach oben. Wir lösen zunächst die letzte Gleichung:

$1z= 1$

$z=\bm{1}$

Jetzt setzen wir den Wert von z in die zweite Gleichung ein, um den Wert von y zu ermitteln:

$-3y+4z=-2 \ \xrightarrow{z \ = \ 1} \ -3y+4(1)=-2$

$-3y+4=-2$

$-3y=-2-4$

$-3y=-6$

$y=\cfrac{-6}{-3} = \bm{2}$

Und das Gleiche machen wir mit der ersten Gleichung: Wir ersetzen die Werte der anderen Unbekannten und lösen nach x auf:

$x+y-z=2 \ \xrightarrow{y \ = \ 2 \ ; \ z \ = \ 1} \ x+(2)-(1)=2$

$x+1=2$

$x=2-1$

$\bm{x=1}$

Die Lösung des Gleichungssystems lautet daher:

$\bm{x=1} \qquad \bm{y=2} \qquad \bm{z=1}$

Übung 2

Finden Sie die Lösung des folgenden Gleichungssystems mit der Gauß-Methode:

$\left. \begin{array}{r} 2x+y+2z=-3 \\[2ex] x+3y+2z=5 \\[2ex] 4x+2y-z=-1 \end{array} \right\}$

siehe Lösung

Als erstes müssen wir die erweiterte Matrix des Systems erstellen:

$\left. \begin{array}{r} 2x+y+2z=-3 \\[2ex] x+3y+2z=5 \\[2ex] 4x+2y-z=-1 \end{array} \right\} \longrightarrow \left( \begin{array}{ccc|c} 2 & 1 & 2 & -3 \\[2ex] 1 & 3 & 2 & 5 \\[2ex] 4 & 2 & -1 & -1 \end{array} \right)$

Um die Gauß-Methode anzuwenden, ist es einfacher, wenn die erste Zahl in der ersten Zeile eine 1 ist. Wir werden daher die Reihenfolge der Zeilen 1 und 2 ändern:

$\left( \begin{array}{ccc|c}2 & 1 & 2 & -3 \\[2ex] 1 & 3 & 2 & 5 \\[2ex] 4 & 2 & -1 & -1 \end{array} \right) \begin{array}{c} \xrightarrow{f_1\rightarrow f_2} \\[2ex] \xrightarrow{f_2\rightarrow f_1} \\[2ex] & \end{array} \left( \begin{array}{ccc|c}1 & 3 & 2 & 5 \\[2ex] 2 & 1 & 2 & -3 \\[2ex] 4 & 2 & -1 & -1\end{array} \right)$

Jetzt müssen wir alle Zahlen unterhalb des Hauptarrays auf 0 setzen.

Also führen wir Zeilenoperationen durch, um die letzten beiden Elemente der ersten Spalte zu ersetzen:

$\left( \begin{array}{ccc|c} 1 & 3 & 2 & 5 \\[2ex] 2 & 1 & 2 & -3 \\[2ex] 4 & 2 & -1 & -1 \end{array} \right) \begin{array}{c} \\[2ex] \xrightarrow{f_2 -2f_1} \\[2ex] \xrightarrow{f_3-4f_1} & \end{array} \left( \begin{array}{ccc|c} 1 & 3 & 2 & 5 \\[2ex] 0 & -5 & -2 & -13 \\[2ex] 0 & -10 & -9 & -21 \end{array} \right)$

Jetzt konvertieren wir das letzte Element der zweiten Spalte auf Null:

$\left( \begin{array}{ccc|c}1 & 3 & 2 & 5 \\[2ex] 0 & -5 & -2 & -13 \\[2ex] 0 & -10 & -9 & -21\end{array} \right) \begin{array}{c} \\[2ex] \\[2ex] \xrightarrow{f_3-2f_2} & \end{array} \left( \begin{array}{ccc|c} 1 & 3 & 2 & 5 \\[2ex] 0 & -5 & -2 & -13 \\[2ex] 0 & 0 & -5 & 5 \end{array} \right)$

Sobald alle Zahlen unterhalb der Hauptdiagonale 0 sind, können wir das Gleichungssystem lösen. Dazu drücken wir die Matrix noch einmal in Form eines Gleichungssystems mit Unbekannten aus:

$\left( \begin{array}{ccc|c} 1 & 3 & 2 & 5 \\[2ex] 0 & -5 & -2 & -13 \\[2ex] 0 & 0 & -5 & 5 \end{array} \right) \ \longrightarrow \ \left. \begin{array}{r} x+3y+2z=5 \\[2ex] -5y-2z=-13 \\[2ex] -5z=5 \end{array} \right\}$

Und wir lösen die Unbekannten der Gleichungen von unten nach oben. Wir lösen zunächst die letzte Gleichung:

$-5z= 5$

$z=\cfrac{5}{-5}=\bm{-1}$

Jetzt setzen wir den Wert von z in die zweite Gleichung ein, um den Wert von y zu ermitteln:

$-5y-2z=-13 \ \xrightarrow{z \ = \ -1} \ -5y-2(-1)=-13$

$-5y+2=-13$

$-5y=-13-2$

$-5y=-15$

$y=\cfrac{-15}{-5} = \bm{3}$

Und das Gleiche machen wir mit der ersten Gleichung: Wir ersetzen die Werte der anderen Unbekannten und lösen nach x auf:

$x+3y+2z=5 \ \xrightarrow{y \ = \ 3 \ ; \ z \ = \ -1} \ x+3(3)+2(-1)=5$

$x+9-2=5$

$x=5-9+2$

$\bm{x=-2}$

Die Lösung des Gleichungssystems lautet daher:

$\bm{x=-2} \qquad \bm{y=3} \qquad \bm{z=-1}$

Übung 3

Berechnen Sie die Lösung des folgenden Gleichungssystems nach der Gauß-Methode:

$\left. \begin{array}{r} 2x+3y+z=-1 \\[2ex] 6x+4y+4z=0 \\[2ex] -4x+2y-z=5 \end{array} \right\}$

siehe Lösung

Als erstes müssen wir die erweiterte Matrix des Systems erstellen:

$\left. \begin{array}{r} 2x+3y+z=-1 \\[2ex] 6x+4y+4z=0 \\[2ex] -4x+2y-z=5\end{array} \right\} \longrightarrow \left( \begin{array}{ccc|c} 2 & 3 & 1 & -1 \\[2ex] 6 & 4 & 4 & 0 \\[2ex] -4 & 2 & -1 & 5 \end{array} \right)$

Jetzt müssen wir alle Zahlen unter dem übergeordneten Array auf 0 setzen.

Also führen wir Zeilenoperationen durch, um die letzten beiden Elemente der ersten Spalte zu ersetzen:

$\left( \begin{array}{ccc|c} 2 & 3 & 1 & -1 \\[2ex] 6 & 4 & 4 & 0 \\[2ex] -4 & 2 & -1 & 5\end{array} \right) \begin{array}{c} \\[2ex] \xrightarrow{f_2 -3f_1} \\[2ex] \xrightarrow{f_3+2f_1} & \end{array} \left( \begin{array}{ccc|c} 2 & 3 & 1 & -1 \\[2ex] 0 & -5 & 1 & 3 \\[2ex] 0 & 8 & 1 & 3\end{array} \right)$

Jetzt konvertieren wir das letzte Element der zweiten Spalte auf Null:

$\left( \begin{array}{ccc|c}2 & 3 & 1 & -1 \\[2ex] 0 & -5 & 1 & 3 \\[2ex] 0 & 8 & 1 & 3\end{array} \right) \begin{array}{c} \\[2ex] \\[2ex] \xrightarrow{5f_3+8f_2} & \end{array} \left( \begin{array}{ccc|c} 2 & 3 & 1 & -1 \\[2ex] 0 & -5 & 1 & 3 \\[2ex] 0 & 0 & 13 & 39 \end{array} \right)$

Sobald alle Zahlen unterhalb der Hauptdiagonale 0 sind, können wir das Gleichungssystem lösen. Dazu drücken wir die Matrix noch einmal in Form eines Gleichungssystems mit Unbekannten aus:

$\left( \begin{array}{ccc|c} 2 & 3 & 1 & -1 \\[2ex] 0 & -5 & 1 & 3 \\[2ex] 0 & 0 & 13 & 39\end{array} \right) \ \longrightarrow \ \left. \begin{array}{r} 2x+3y+1z=-1 \\[2ex] -5y+z=3 \\[2ex] 13z=39 \end{array} \right\}$

Und wir lösen die Unbekannten der Gleichungen von unten nach oben. Wir lösen zunächst die letzte Gleichung:

$13z= 39$

$z=\cfrac{39}{13}=\bm{3}$

Jetzt setzen wir den Wert von z in die zweite Gleichung ein, um den Wert von y zu ermitteln:

$-5y+z=3 \ \xrightarrow{z \ = \ 3} \ -5y+(3)=3$

$-5y=3-3$

$-5y=0$

$y=\cfrac{0}{-5} = \bm{0}$

Und das Gleiche machen wir mit der ersten Gleichung: Wir ersetzen die Werte der anderen Unbekannten und lösen nach x auf:

$2x+3y+1z=-1 \ \xrightarrow{y \ = \ 0 \ ; \ z \ = \ 3} \ 2x+3(0)+1(3)=-1$

$2x+0+3=-1$

$2x=-1-3$

$2x=-4$

$x=\cfrac{-4}{2}=\bm{-2}$

Die Lösung des Gleichungssystems lautet daher:

$\bm{x=-2} \qquad \bm{y=0} \qquad \bm{z=3}$

Übung 4

Lösen Sie das folgende Gleichungssystem mit 3 Unbekannten mit der Gauß-Methode:

$\left. \begin{array}{r} 2x-6=4y+6z \\[2ex] -y-3z=1-3x \\[2ex] -4x-y=6-3z \end{array} \right\}$

siehe Lösung

Bevor wir die Gauß-Methode anwenden, müssen wir das Gleichungssystem so anordnen, dass sich alle Unbekannten auf der linken Seite der Gleichung und die Zahlen auf der rechten Seite befinden:

$\left. \begin{array}{r}2x-6=4y+6z \\[2ex] -y-3z=1-3x \\[2ex] -4x-y=6-3z \end{array} \right\} \longrightarrow \left. \begin{array}{r} 2x-4y-6z=6 \\[2ex] 3x-y-3z=1 \\[2ex] -4x-y+3z=6\end{array} \right\}$

Sobald das System geordnet ist, erstellen wir die entwickelte Matrix des Systems:

$\left. \begin{array}{r} 2x-4y-6z=6 \\[2ex] 3x-y-3z=1 \\[2ex] -4x-y+3z=6 \end{array} \right\} \longrightarrow \left( \begin{array}{ccc|c} 2 & -4 & -6 & 6 \\[2ex] 3 & -1 & -3 & 1 \\[2ex] -4 & -1 & 3 & 6 \end{array} \right)$

Da alle Zahlen in der ersten Zeile gerade sind, teilen wir die erste Zeile durch 2, bevor wir mit den Zeilen arbeiten. Dies erleichtert die Berechnungen:

$\left( \begin{array}{ccc|c}2 & -4 & -6 & 6 \\[2ex] 3 & -1 & -3 & 1 \\[2ex] -4 & -1 & 3 & 6 \end{array} \right) \begin{array}{c} \xrightarrow{f_1/2} \\[2ex] \\[2ex] & \end{array} \left( \begin{array}{ccc|c}1 & -2 & -3 & 3 \\[2ex] 3 & -1 & -3 & 1 \\[2ex] -4 & -1 & 3 & 6\end{array} \right)$

Jetzt müssen wir alle Zahlen unterhalb des Hauptarrays auf 0 setzen.

Also führen wir Zeilenoperationen durch, um die letzten beiden Elemente der ersten Spalte zu ersetzen:

$\left( \begin{array}{ccc|c} 1 & -2 & -3 & 3 \\[2ex] 3 & -1 & -3 & 1 \\[2ex] -4 & -1 & 3 & 6 \end{array} \right) \begin{array}{c} \\[2ex] \xrightarrow{f_2 -3f_1} \\[2ex] \xrightarrow{f_3+4f_1} & \end{array} \left( \begin{array}{ccc|c} 1 & -2 & -3 & 3 \\[2ex] 0 & 5 & 6 & -8 \\[2ex] 0 & -9 & -9 & 18\end{array} \right)$

Da alle Zahlen in der letzten Zeile ein Vielfaches von 9 sind, teilen wir sie wie zuvor durch 9, um die Berechnungen zu vereinfachen:

$\left( \begin{array}{ccc|c}1 & -2 & -3 & 3 \\[2ex] 0 & 5 & 6 & -8 \\[2ex] 0 & -9 & -9 & 18 \end{array} \right) \begin{array}{c} \\[2ex] \\[2ex]\xrightarrow{f_3/9} & \end{array} \left( \begin{array}{ccc|c}1 & -2 & -3 & 3 \\[2ex] 0 & 5 & 6 & -8 \\[2ex] 0 & -1 & -1 & 2\end{array} \right)$

Jetzt konvertieren wir das letzte Element der zweiten Spalte auf Null:

$\left( \begin{array}{ccc|c}1 & -2 & -3 & 3 \\[2ex] 0 & 5 & 6 & -8 \\[2ex] 0 & -1 & -1 & 2\end{array} \right) \begin{array}{c} \\[2ex] \\[2ex] \xrightarrow{5f_3+f_2} & \end{array} \left( \begin{array}{ccc|c} 1 & -2 & -3 & 3 \\[2ex] 0 & 5 & 6 & -8 \\[2ex] 0 & 0 & 1 & 2 \end{array} \right)$

Sobald alle Zahlen unterhalb der Hauptdiagonale 0 sind, können wir das Gleichungssystem lösen. Dazu drücken wir die Matrix noch einmal in Form eines Gleichungssystems mit Unbekannten aus:

$\left( \begin{array}{ccc|c} 1 & -2 & -3 & 3 \\[2ex] 0 & 5 & 6 & -8 \\[2ex] 0 & 0 & 1 & 2 \end{array} \right) \ \longrightarrow \ \left. \begin{array}{r} x-2y-3z=3 \\[2ex] 5y+6z=-8 \\[2ex] 1z=2 \end{array} \right\}$