Hier erklären wir, wie man eine Potenz (oder Potentialfunktion) ableitet, Sie finden die Formel zur Ableitung einer Potenz, mehrere Beispiele und können sogar mit Schritt für Schritt gelösten Übungen üben.
Formel für die Ableitung einer Potenz
Die Ableitung einer Potenz oder potentiellen Funktion ist das Produkt aus dem Exponenten der Potenz mal der Basis erhöht zum Exponenten minus 1 mal der Ableitung der Basis.
![]()
Wenn die Basis also die Identitätsfunktion ist, multiplizieren Sie einfach die Funktion mit dem Exponenten und subtrahieren Sie eine Einheit vom Exponenten, um die Potenz zu erhalten:
![]()
Tatsächlich ist die Ableitung der Identitätsfunktion gleich 1.
Zusammenfassend lässt sich sagen, dass es zur Ableitung einer potentiellen Funktion zwei Formeln gibt: die erste, die immer verwendet werden kann, und die zweite, die nur angewendet werden kann, wenn die Basis ein x ist.
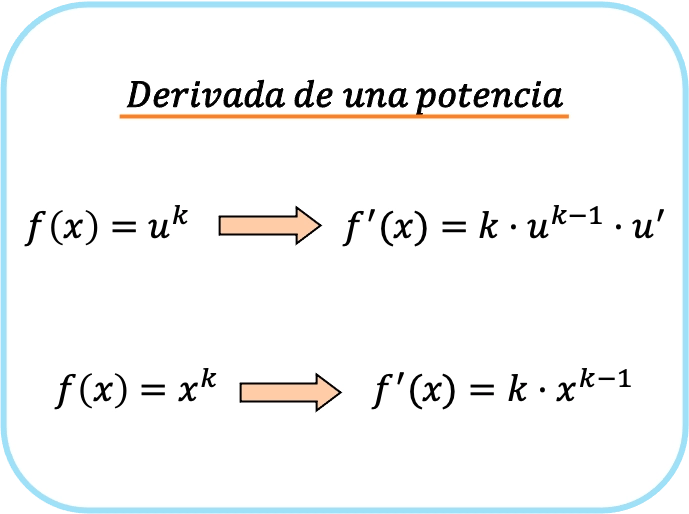
Wir können leicht überprüfen, dass die erste Formel für die Ableitung einer Potenz der zweiten entspricht, jedoch die Kettenregel anwendet.
Beachten Sie, dass diese Formeln nur verwendet werden können, wenn die Variable die Basis der Potenz ist. Wenn das x im Nenner steht, müssen Sie die Regel für die Ableitung einer Exponentialfunktion anwenden:
➤ Siehe: Ableitung einer Exponentialfunktion
Beispiele für Stromderivate
Nachdem wir die Formel für die Ableitung einer potentiellen Funktion gesehen haben, erklären wir einige Beispiele dieser Art von Ableitung, damit Sie verstehen, wie Potenzen abgeleitet werden.
Beispiel 1: Ableitung einer Basispotenz x
![]()
Wie wir im vorherigen Abschnitt erläutert haben, lautet die Formel, die wir zur Ableitung der Funktion verwenden müssen, wenn die Basis der Potenz nur ein x ist:
![]()
Die Ableitung der Potenz x hoch 4 ist also:
![]()
Beispiel 2: Ableitung einer Potenz mit Klammern
![]()
In diesem Beispiel ist die Basis nicht die Identitätsfunktion, wir müssen daher die allgemeine Formel für die Ableitung einer Potenz verwenden:
![]()
Die Funktion in Klammern ist eine lineare Funktion, daher ist ihre Ableitung 2. Daher ist die Ableitung der gesamten potentiellen Funktion:
![]()
Beispiel 3: Ableitung einer negativen Potenz
![]()
In diesem Fall haben wir eine potentielle Funktion, deren Exponent negativ und deren Basis ein Logarithmus ist. Daher verwenden wir die folgende Formel, um die Funktion zu differenzieren:
![]()
Auch wenn der Potenzexponent negativ ist, muss auch eins davon subtrahiert werden. Die Ableitung der Funktion lautet daher:
![]()
Wenn Sie Zweifel an der Lösung haben, können Sie hier die Formel für die Ableitung einer logarithmischen Funktion einsehen:
➤ Siehe: Ableitung einer logarithmischen Funktion
Beispiel 4: Ableitung einer Potenz mit Wurzel
![]()
Die Funktion in diesem Beispiel ist eine Potenz innerhalb eines regulären Ausdrucks. Radikale können jedoch in potentielle Ausdrücke umgewandelt werden, sodass die Funktion vereinfacht werden kann, indem man sie in eine potentielle Funktion mit einem gebrochenen Exponenten umwandelt:
![]()
Wir wenden nun die Formel für die Ableitung einer Potenz einer Variablen an:
![]()
Und die Ableitung ist:
![]()
Sie können diese Funktionstypen auch mithilfe der Wurzelableitungsregel unterscheiden:
➤ Siehe: abgeleitet von einer Wurzel
Gelöste Übungen zur Ableitung einer Potenz
Berechnen Sie die Ableitung der folgenden Potenzen:
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
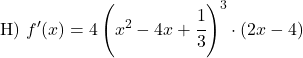
![]()